> Техника, страница 89 > Физика и технология трения в машинах

Физика и технология трения в машинах

Физика и технология трения в машинах. 1) Гидродинамическая теория смазки. Теория трения хорошо смазанных тел (гл. обр. шипа в подшипниках) была создана русскими учеными. Первенство в этом деле принадлежит Н.П. Петрову,военному инженеру, к-рый в 1883 г. напечатал капитальное исследование о трении и смазке и положил начало гидродинамич. теории трения. Его идеи были значительно развиты и получили новую с математической стороны разработку трудами Η. Е. Жуковского и С. А. Чаплыгина. В иностранной литературе после Петрова выступил Осборн Рейнольдс (1887 г.); далее Зоммерфельд (1904 год), давший приближенное решение гидродинамических уравнений движения вязких жидкостей; в ответ на эту работу и была напечатана работа Η. Е. Жуковского и Чаплыгина (1904 год), дающая полное (в пределах возможности интегрирования уравнений) решение соответственных уравнений.

Построение теории идет следующим путем. Так как между шипом и подшипником находится смазывающая среда и трение жидкого слоя о жидкий слой меньше, чем трение между сухими телами, то практически нужно, чтобы одна часть смазывающего слоя прилегала к неподвижному элементу пары шип—подшипник, а другая к подвижному. Следовательно нек-рая часть слоя будет вместе с подшипником неподвижна, другая же часть должна вращаться вместе с шипом, имея скорость относительно шипа, равную пулю. Практически это достигается подбором смазочного материала сообразно материалам шипа и подшипника (или вкладыша). Т. о. при рассмотрении движения слоя теория заранее предполагает, что скорость элементов слоя и подшипника равна нулю, а у шипа равна окружной скорости шипа. Затем теория предполагает, что давление по длине шипа располагается однообразно, то есть если мы проведем какое-нибудь сечение, перпендикулярное к оси пары, и в нем найдем распределение давления на подшипник соответственно различным направлениям радиусов его (полярная диаграмма давлений), то и в другом каком-либо параллельном сечении распределение давлений будет то же самое. Этим предположением теория отбрасывает влияние третьей координаты (вдоль оси пары) и сводит задачу к рассмотрению так называемым плоского движения. Не нужно думать, как это часто встречается у авторов, пишущих по трению между шипом и подшипником, что теория предполагает бесконечно длинный шип. Наблюдения показывают, что короткий, но очень мало деформирующийся шип более удовлетворяет требованиям теории, нежели длинный и легко изгибающийся. Давление в каком-либо осевом сечении падает разумеется к концам его, то есть к концам подшипника, но оно может падать круто или отлого. В первом случае предложения теории более удовлетворяются, нежели во втором. Это именно и наблюдается в сравнительно коротких, но недеформирующихся шипах, тогда как в длинных, но перегруженных распределение давления по длине далеко уклоняется от требований теории. Т. к. интегрирование соответствующих ур-ий в трех измерениях представляет трудность и м. б. произведено лишь при известных произвольных предположениях, то практичнее остановиться на рассмотрении плоского движения и введением поправочных опытных коэф-тов приблизить выводы теории к действительности. На том же основании и в рассмотрении плоского движения теория должна ограничиться лишь наиболее простыми соотношениями и в определении постоянных, входящих в эти соотношения, должна оставлять некоторый (разумеется небольшой) произвол, чтобы последующими опытными данными ограничить этот произвол сообразно с опытом. Таким образом правильно поставленная теория является руководительницей опытов, указывая, в каком направлении их вести и какие величины должны быть определены. К сожалению, как это видно будет из последующего, многие опыты являются малоценными, так как в них не были тщательно измерены именно те величины, без знания которых заключения с точки зрения теории являются сомнительными. Ниже указаны требования теории относительно постановки опытов.

Итак, сведя все к движению в двух измерениях и воспользовавшись общими ур-иями дви жения вязкой жидкости, мы получим ур-ие в частных производных второго порядка. Общие ур-ия движения вязкой жидкости, как и общие ур-ия теории упругости, были впервые даны Навье, к-рый весьма просто их вывел на основании рассмотрения молекулярных взаимодействий. Т. к. последующие авторы предпочли рассматривать упругое тело как сплошную среду и вместо молекулярных взаимодействий ввести рассмотрение натяжений в упругом теле, то и в выводе ур-ий для движения вязкой жидкости обычно идут теперь тем же путем, как это в кратком изложении и указано ниже. Т. о. мы приходим к ур-иям типа

du _ др_хх др_х}/ др_х1“ dt Ох ^[ ду dz ’

если пренебрежем силой тяжести (смотрите ниже). Но кроме силы тяжести мы пренебрегаем затем и силой инерции смазывающего слоя. Это пренебрежение вызывало частые возражения, однако оно вполне сообразно с опытом. Дело в том, что, как мы увидим далее, смазывающий слой в современных конструкциях имеет весьма незначительную среднюю толщину, и понятно, что его инерция ничтожна сравнительно с теми натяжениями, какие в нем развиваются от внешнего давления. Таким путем, принимая во внимание еще условия несжимаемости жидкости, мы приходим к основному ур-ию 9²р. з“р ₀9*2 ¹ ау2

Но, как было уже указано, сюда необходимо присоединить еще граничные условия. Т. к. границами служат шип и подшипник, являющиеся в сечении окружностями, то необходимо представить эти окружности простейшими соотношениями, а для этого, неизбежным будет изменить систему координат. Окружности шипа и подшипника не будут концентричными, т. к. всегда между их радиусами существует, хотя и очень малая, разница, внешнее же давление стремится прижать шип к окружности подшипника. Поэтому мы всегда имеем дело с двумя эксцентричными окружностями, хотя эксцентриситет и м. б. очень малым. Но тогда удобным является применить координаты Неймана, о которых подробно сказано ниже (фигура 1). Именно благодаря введению этих координат Η. Е. Жуковский и С. А. Чаплыгин и подошли быстро к решению задачи, что не удавалось ни Рейнольдсу ни Зоммерфзльду, и только двадцать лет спустя в иностранной литературе появилось решение, более полное, чем у Рейнольдса.

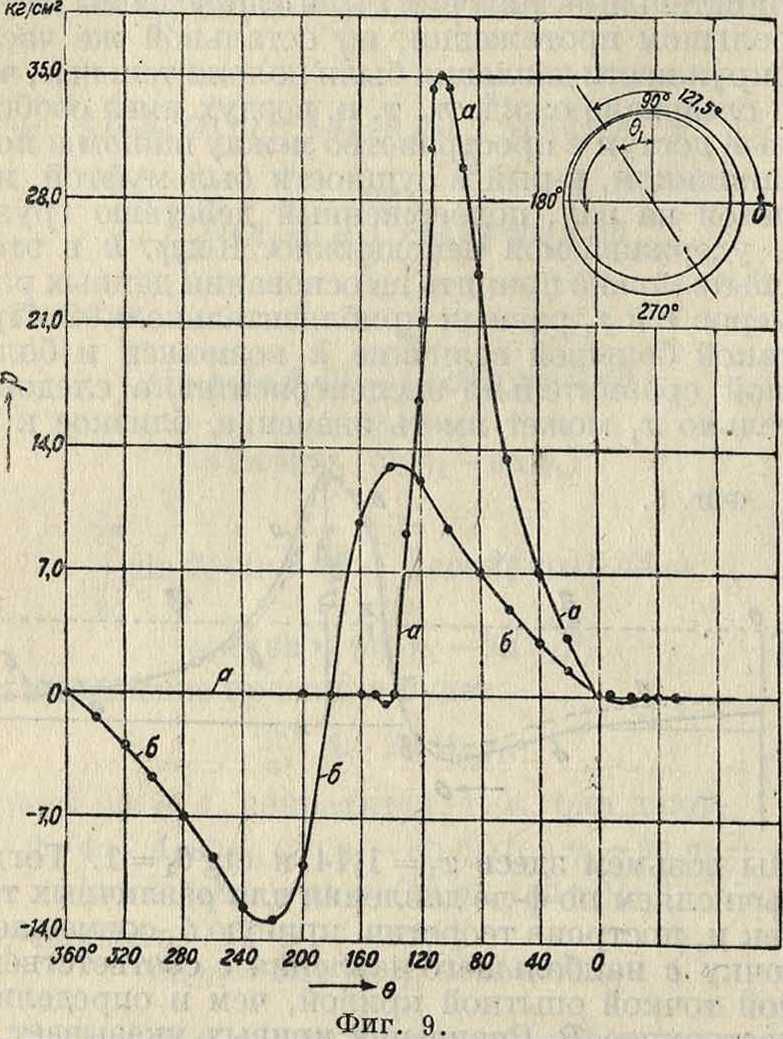
В настоящей статье решение Η. Е. Жуковского и С. А. Чаплыгина мною несколько расширено. Применение координат Неймана дает возможность сразу же видеть ложную постановку опытов например с большим сравнительно эксцентриситетом. В дальнейшем представляется необходимым для решения задачи ввести ф-ию тока и при помощи ее выразить граничные условия. Эта ф-ия может иметь б. или м. сложный вид. Жуковский и Чаплыгин выбрали простейший вид, удовлетворяющий граничным условиям. Автором сообразно опытам этот вид несколько расширен, благодаря чему появилось согласие между опытной и теоретич. картинами распределения давления на подшипник. Но выражение коэф-та трения осталось простым. Правда, в формуле распределения давления на подшипник имеется одна величина (ctg6₁), к-рую нужно брать по опытам. Там, где она дается опытом, теоретич. картина распределения давления хорошо согласуется с опытной. Это и указывает на рациональность введения этой величины, и когда из опытов видна будет зависимость ее от различных условий, можно будет заранее точно выяснить фактич. картину распределения давления по подшипнику. Но и теперь, как указывают примеры, взяв нек-рую среднюю величину для ctg 0_Х, можно выяснить заранее, насколько рационально или нерационально будет работать данная установка. Главенствующее значение в этом отношении играет другая величина, зависящая от разности между радиусами шипа и подшипника и обозначенная в тексте через x_t. Здесь можно указать на два примера, приведенные в тексте. Один— указанное Бредфордом и названное им типическим распределение давления по подшипнику (фигура 9); в этом случае х_х, как видно из приведенных в тексте опытных величин, можно взять равным 1,4, далее по наблюденному отклонению линии центров ctg0_x=l,3, и затем вычисляется по формуле текста распределение давления, хорошо согласующееся с опытным (фигура 9а). В другом опыте с той же парой вследствие уменьшения эксцентриситета х_гполучило величину, равную 1,6, ctg 0_г — 0,854, и диаграмма давлений (фаг. 10) указывает на большую равномерность распределения именно вследствие увеличения х₁. Противоположный пример представляет опыт, описанный у Стентона, где, как видно из текста, *!=1,0015 вследствие большой разности между диаметрами шипа и подшипника. Тогда, принимая ctg θ₁=1, получаем кривую распределения давления, весьма отличающуюся от других (фигура11), и здесь на очень ограниченном пространстве имеем резкий скачок давления от отрицательного максимума к положительному, остальная же часть поверхности подшипника почти не участвует в восприятии давления. Т. о. нерациональность малой сравнительно величины ж_х наглядно указывается теорией. Отсюда следует, что при предварительных расчетах нужно величину £C₁ брать близкой к 2, и, предложив какое-нибудь среднее значение в_и подсчитываем допускаемую нагрузку р на единицу длины и исправляем ее опытным коэф-том на распределение давлений по длине подшипника. Таким путем можно обеспечить конструкцию от горения масла.

Гидродинамич. ур-ия движения вязкой жидкости аналогичны соответственным ур-иям для упругого тела. В обоих случаях должен быть рассмотрены относительные перемещения частиц среды, которые вызывают соответственные силы натяжения или сопротивления. Принимают в целях возможного упрощения задачи, что эти натяжения являются линейными ф-иями перемещений. Возьмем какие-нибудь две соседние точки среды с координатами х, у, z и x+dx, y+dy, z + dz; вектор, их соединяющий, будет иметь длину

ds³=dx³ -f йу^г + dz².

Диференцируя, найдем его изменение через промежуток времени di, к-рое будет определяться ур-ием ds б ds=dx δ dx + dy δ dy + dz δ dz, но, называя скорости точки (ж, у, г) по осям X, Υ, λ через и, », w, будем иметь ее координаты через времяdi:a;+wdfHT. д.,аточки x+dx и т. д. x + dx+(u+du) dt и т. д., следовательно

δ dx=dudt=dx + ~ dy + ~ dz} dt

и аналогично для остальных координат. Т. о.

dw ~dz

^dsSds==[^^dx2 + ^;^dy² + ^)dz² +

η _Ί (ди. dv. _Ί, (ди, dw

- ^{dx d}v lw + te) + ^{dx dz} ( βϊ + βϊ)

6ds ds dt

м du n -=-^-a²

OX

dy dz ^·

By

dv, dz "*

dV9

~dz

dw

dy

?)]“>

+«/>(!“

-i- -xii +

. (du, dw. о (dv

+ “>^,.Ы+ to) +Pv Ы

dy

By ¹ Ox! 9w

By)

где α, β, у—косинусы углов вектора с осями. Левая часть равенства представляет отношение изменения длины вектора к начальной длине и ко времени dt и называется растяжением в единицу времени. Геометрическим местом точек,

для которых=Const, будет поверхность второго порядка, и оси ее называются главными осями растяжений. Ур-ие поверхности, отнесенное к главным осям X, Y, Z’, будет

%dx²+ ^dy²+^:dz²

Const — я-;ί -Γ 7Γ> Μ-я I _я,

Οχ ¹ By ^α αζ

и соответственно растяжение а какого-нибудь вектора, делающего с осями углы с косинусами а, β, у, выразится ф-лой ди

α=

дх су·

где а, b, с —растяжения по главным осям. Растйжения b и с для двух между собою и к а перпендикулярных направлений представляются аналогичными ф-лами:

откуда и т. к.

b=аа“ + b		β"2 + (.γ"*	>
с — аа"	2+ Ь	>§"* + су"2,
а + b	+ с =	а + V + с	»
	7, _	dv dw
дх	, и =	ду’ °~Ύζ	»
г, и, V,	w относятся к осям а, 1
i. : 1 ду ~	dw dz ~	du j dv, dx 1 ~ay ‘	dw l)z‘	9
( δ dx	ди	δ du du	_	ddz
’ dx dt )5	ду ~	dydt )’ dz	“I	,dzdt )

ди дх НО

дх и следовательно ди, dv. dw _ 6(dx dydz) дх ду dz dxdydz

что равно увеличению объёма. С другой стороны, мы можем выразить суммы производных, входящих в ур-ие растяжения, через растяжения по главным осям, напр -§~ + ^· Имеем и=иа + + ν β + wy по теореме о проекциях, и далее д д, д _ог, д ду

1_

dt

δάν

dv

1

dt⁹

a" +

так же

«, R" J_ JL y"

dx dy ^ ¹ dz * *

V=ua" + νβ" + wy";

/·

d o,. d dy ^P ^ dz

% + T_X=2 aaa" + 2 bPfi" + 2 eyy

подобным же образом находятся и две другие суммы. Рассмотрим теперь в среде бесконечно малый параллелепипед со сторонами dx dy dz. На Каждую грань действуют давления (или натяжения) со стороны соседних с ним элементов среды, вызванные относительными перемещениями частиц среды. Обозначим через р_хх давление на грань, перпендикулярную к оси X, действующее в направлении оси X, а через р_ху, Vxz—давления (или напряжения), действующие на ту же грань в направлении двух других осей, т. ч. результирующее давление вообще не будет нормально к грани. Но для главных осей растяжений давление на грань, перпендикулярную к оси, будет направлено по оси (для изотропного тела), и принимается, что это давление будет линейной ф-ией растяжений. Т. о. аналогично тому, как найдены были растяжения по трем взаимно перпендикулярным направлениям через растяжения по главным осям, мы можем здесь написать, называя давления по главным осям через р_х, р₂, р₃,

Vxx — Ρι^{α 2} Т Ρζβ ² ~Ь РзУ ²> Vyy

= р_ха"² + рз,

-· Ρχα"² + Ρζβ² + "² + Рз/"²

и так же получим

Vxx + Vyy + Vzz=Pi + Ра + ϊ>3=3 р_:где р—среднее давление в данной точке. Т. к. слагающая р_ху происходит от боковых смеще-« ди, dv НИЙ ~х

By

ΘΓ’^Τ0

Vxy=Ριαα" + p₂ ββ" + Р-Уу"; подобным же образом выразятся ρ_χζ и p_yz. и мы видим, что р_Ху=р_ух и p_yz=Pzy Теперь напишем, что давление p_L отличается от среднего на линейную ф-шо растяжений, то есть

Pi=р - Λ (а + b + с) — 2 μα, и подобным же образом

Рα= р — Λ (а + Ь + с)-2 μΐ), р₃=р - A (a + b + с) — 2 μβ

при условии ЗА + 2 д=0. Подставляя эти значения в выражения для р_хх и т. д. и принимая во внимание значения растяжений в ф-ии а, V, с получим

~)ц, dv, dw ₀ ди ду

Vxx V + и т. д.,

+SH

а.т

Производя действия и принимая во внимание, что для главных осей (по свойству осей поверхностей второго порядка)

dv, ди ди _i dw dv, dw

dx ^_г ду ~ ~~ dz ¹ dx ~~ ~dz ¹ ~dy ’

найдем

^ (du, dv

Vxy - V [щ; + θΐ)

и т. д. и для несжимаемой жидкости имеем условие ди, dv. dw _,-, дх ду dz

С другой стороны, рассматривая условие дииа-мич. равновесия бесконечно малого параллелепипеда и пренебрегая силой тяжести, найдем

В Рхх I ЦРух_ i BPzx_ В Ρχχ. д Рх_У, Βρχζ

Ох ¹ By dz ~ дх ^ ду ¹ dz

И Т. Д.

Примем жидкость несжимаемой и пренебрежем силами инерции, к-рые, как показывает опыт, ничтожны в смазывающем слое. Тогда по подстановке выражений р_ет и т. д. через смещения получим ур-ия:

1 др.

— Ди,

μ дх

du

етг

1 др ~м~ду~ 1 др μ dz ‘

Αν,

Aw,

где Δ =

02, 02 0ж2 + 0^2

ч ди. dv

са) и условие ^ + ^

(знак оператора Лапла-0ш

0z

= 0.

Рассмотрим движение плоское и следовательно ограничимся двумя осями×и Y. Для случая шипа и подшипника это означало бы, что мы пренебрегаем изменением условий движения смазывающего слоя к краям подшипника. Тогда можно преобразовать ур-ия, введя угловую скорость ω вихря, имеющего место в движении жидкости. По основным соотношениям гидродинамики (смотрите) имеем

_rt ди dv

^гсо=д_У—ш

и следовательно

Отсюда д²и, д²и дх² ^ ду² "

02 со ду

02(о	0 2li	d2v
дх	_ 0х ду	дх2 5
02(о _	_ д“и _	02υ
ду	“ 0уа	дхду
, 02U	02U	02ω	+ -	/0U
г 0Х2	1 0х ду	_ ду	~ 0Х	0х 1

dv

ду)

А^!Р + £!?=д«=0

дх² ду² I

и также Δ2 ω=0.

Прежде чем разбирать эти ур-ия, необходимо для удобства решения задачи о движении слоя между шипом и подшипником изменить систему координат. Введем систему биполярных координат Неймана (Neuman). Здесь берутся два полюса F и F на оси×на расстояниях +а и — а от начала координат (фигура 1); положение любой

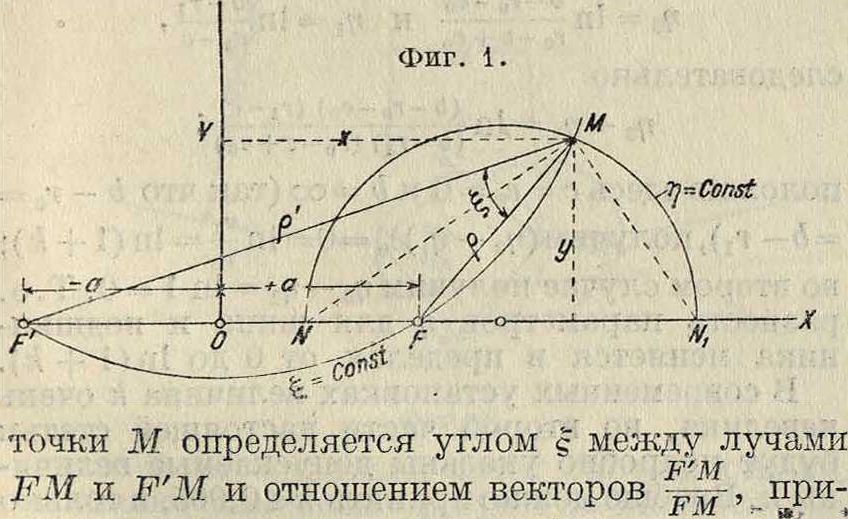
чем вместо самого отношения берется величина η --= 1η=In j· · При данных ξ и η положение точки М определится,если: 1) найдем геометрии, место точек М, отношение расстояний которых до точек F’ и F равно данной величине, т. e. =e^v’ как; известно из элементарной геометрии, этим геометрич. местом будет окружность, имеющая диаметром отрезок NN₁ (фигура 1), где NF N-lF

NF ~ iN_tF

и 2) опишем окружность, вмещающую данный угол ξ, на отрезке FF. Т. о. кривые »?=Const для различных значений Const—окружности,

-~~=с в ди, dv

и на основании условия щ

02и. д²и_ д _02ω

д& + ^{_ ЛМ} - ду ^-

„. о _А 02 а>

Таким же путем найдем Δ»=— -_д~, вательно ур-ия движения жидкости напишутся

1 др 02 ω 1 др 02 ω

~μ Ί)Χ ду μ ду дх

Они дают ур-ие

= 0 получим и следо имеющие центры на оси ОХ и диаметрами различные отрезки NN_U а кривые ξ= Const—окружности сцентрами на OF, проходящие через точки FF. Удобство этих координат для данной задачи заключается в том, что как окружность подшипника, так и окружность шипа, расположенная вообще эксцентрично с первой, характеризуются двумя значениями η=η₁ и η=η₀· По данному значению η радиус окружности найдется сл. обр.:

N_tF e _ NF _2a-NF_

NF

NiF + 2 а отсюда и NF-

NF 2 а

—+1

NiF + FN=2 г =

4а ---

* ( ч

shi)

Разность радиусов

(-Ы ¹

-г₀=а

δ

Vshj)! sh>)o sj>i)_t

шипа и подшипника:

V ^г°

(shJ?₀ — sh%)=6,

и, назвав — через 7с, получим sh η₀=(1 + 7;)sh ^r0

расстояние центра какого-нибудь круга от начала координат:

а + г — NF — а +

2а е-п-_е~У _еЧ + 1

[(_е*7__е-*7)(_е»7 + 1)+2(е^ +1) —2(е^ -e^-7?)]

— а

(e⁷!-e ^rl)(e^ri+l) (e»7_+e—«7)(β*?+1)

—=a cth η,

(вЧ-е-.^)(вЧ+1)

следовательно эксцентриситет между шипом и подшипником

ash(i)₀-»)i) r₀shff

~ — o>

a (cth ηχ — cth i?o)^:

Sil η i Sh η_₀

где ο=η₀ — η_ΐ9 и отношение е₀ _ sh a _ sh σ

shi?_:

δ " sh ))<i-sh vi fe sh j)i

Точно так же найдутся координаты х ж у в ф-ии ξ и »?; из тр-ка FMF имеем

4 «²=ρ² + ρ² — 2 ρρ COS ξ И ρ²=ρ² -f 4 a² +

4- 4 α (ж — α), т. e. 4α®=ρ² —ρ².

Отсюда

ρ² —ρ²

ρ 2 + ρ2_2ρρ COS

Щ

1 ρ 1

- — η—7 V -^C

4^е ii

sh i?

ch i?- COS ξ

ashy ₀

то есть ж=—--_og-j, далее 2 a?

ρ ρ Sin§, И a sin I

’ ch p-COS I *

ch η-cos

разделении на 2a получим y=ставим производную от р по ξ:

др_др дх, 0р. 0г

~ дх βξ Т. ду ,.0£ др sh »7 sin ξ _j_ dp_ (ch у cos 1-1) ду (ch 77-cos ξ)².

ПО

Co-

_ Г_

^ 03C (ch y —cos £)²

Но, с другой стороны,

]·

д-2 о) ду д2о) l-ch?7Cos|·

02(о дх ^ 02(о ду дх ду ¹ ду ду

02(о sh у sin ξ

дх (ch у —cos s)² ду (ch?7-cosl)²

и так как др д?(о

Οχ ^μ ду ’ др

~д£

др _ ду ~

02 о)

^:μΊΪ

-/<

02ω

дх то есть м д²р _А 0*2ω, 9²?ω _{0 л}

+ ё;=VP=^{0 и} мг -г ~ΰηΐ=ν2ω=0.

и так же

0р 02(о.

~дп ⁼ ~ ^μΊ>(’

следовательно получим основные ур-ия в £ и η:

д²р θξ 2

Т. к. тригонометрические sin и cos меняют свой знак последвукратногодиференцирования, гиперболические же остаются без изменения, то ур-ию для р мы можем удовлетворить, взяв суммы произведений

Σ А_п sin (ηξ + α„) sh щ,

Σ A_n sin (ηξ + α„) ch (τ - пц)

и тому подобное., где а_п и τ—нек-рые постоянные.

Предположим, что мы отыскиваем распределение давления на подшипник. Полагаем V=если теперь положить <*„=0, то первые два типа сумм дадут давление на подшипник, равное 0 при £=0 и £=π. Ат. к. оба значения £ соответствуют линии центров, именно £=0 для точки Νχ и £=π, для точки Ν, то давления на подшипник в обеих точках на линии центров, то есть в самом широком месте смазочного слоя (точка Νχ) и в самом узком месте (точка Ν), равняются нулю, по обе же стороны линии центров давление м. б. симметричным: по одну сторону положительным, по другую отрицательным. Такое распределение, как наиболее простое, и было принято Η. Е. Жуковским и С. А. Чаплыгиным, и в виду отсутствия тогда опытных данных по распределению давления на подшипник оно казалось наиболее естественным. В настоящее время имеется ряд таких опытов, и хотя они и не удовлетворяют вполне требованиям теории и не отвечают на все ее вопросы, но в общем дают указание, что давление на подшипник расположено не симметрично. Поэтому в наиболее простом виде давление представится формулой:

ρ=Βχ sin £ + В₂ cos £ + B)Sin2£-f + B₄cos2£ + B₅,

где Βχ, В_г, В_ЗУ Βχ—гиперболич. ф-ии, которые на подшипнике, где η=η_χ, обращаются в постоянные, а В₅—постоянное. При опытах м. б. определен эксцентриситет е₀, тогда можно определить положение полюсов координат Неймана. Пусть расстояние одного полюса координат F (ближнего) от центра круга г_х будете, а другого, дальнего, F’ будет b, тогда имеем для точек окружности радиуса г_х соотношение:

b + г _ρ _b-Τχ

С + Г1 ρ ^— Г-С ⁹

то есть

bс=г |.

Для окружности радиуса г_с (шипа) получим так же

(с - е„) (b - е₀)=г²=Ьс - е₀ (b -f с) + е,

то есть

_и2 A g2

_с ,Λ .ν’-Λ.

«о

Отсюда для определения bя с имеем ур-ие

2 +=0,

-г“ + е

2е₀

один корень дает

^L±j/I

2е₀

Ь и другой с.

2 2

·-) -П; Затем

^t‘-^fi ₌<L ₌ P Γι-с e

чем и определится параметр ника, так же для шипа ь

η_χ для подшип-

,Чо ₌ Ц-Гр-вр

Т. к.·

^:=а, то г_х sh ηχ

r₀-c + e„ b-c

2 ’ b+c

и следовательно

(ch² — sh² ηχ=1) Τχ ch ηχ=-γ-. Так же можно определить угол £ в ф-ии угла 0, к-рый делает радиус г_х, идущий к данной точке окружности r_t, с линией центров. Для координаты х этой точки имеем, с .одной стороны,

и,—с другой,

отсюда

X=Τχ cos θ +

shr;i

b + с

cii»?i-cos£

α,

cos ξ =

и следовательно

sin ξ=-

2r₁cos6 + ь + c

(b-c) sin Θ

2 Τχ cos Θ + b + c

При этом 0=0, где £=0, т. e. в самом широком месте слоя, и (=жи9=я в самом узком месте. Т. к. наибольшее значение sin£ есть 1, то, продиференцировав выражение sin £ по 0, найдем значение 0 для £ =

Из условия —^ ^=0

получим cos 0 =,

т. e.

сΙβ

О > i для £=I. Ве личина эксцентриситета может меняться от 0 до ό или по отношению к радиусу г₀ от 0 до к. В первом случае Ь=ооис=0,во втором случае, как видно из выражения для z, b=с=Τχ. Соответственно этому будет меняться и разность Vo — Vi параметров шипа и подшипника. Имеем т b-r_Q — e о i b-Τχ

η₀=In —¹ и ηχ=In--¹,

следовательно с + Со

(Ь-г„-е₀) (tv—е)

(Ь— г_х) Цр-с + ер)

положив здесь с=е₀=Ои6=оо (так что b — г₀ —=b- Τχ), получим(η_α - ηχ)β₀=0=In ^=In (1 + к);

во втором случае получим η₀ — ηχ=In 1=0. Т.о. разность параметров η для шипа и подшипника меняется в пределах от 0 до In (1 -4- 7с).

В современных установках величина к очень невелика, во второй части настоящей статьи будут подробно указаны допускаемые величины к. Вообще можно принять ,005, и только в исключительных случаях к бывает больше этой величины. Тогда величина η₀ — ηχ=β всегда будет малой и всегда с достаточной степенью точности можно положить sh а—о и cher=l.Пользуясь тою же малостью к, мы можем и эксцентриситету дать приближенное выражение. Имеем ур-ие г2 —_1_ р2.

Ь +с=- ^{1 0 0}

отсюда

^ео

~е₀(b +с) + г“-г“=0, но

rl-rt=rt(l + ky-rt=2rlk, если мы пренебрежем второю степенью к.

Таким образом имеем:__

_{ео =} ^_]Л^-2г§А: =

Ь + с Ь+с Г, ^8r0^fe l*^ —

- —--“L¹ (ы-с)^

2 r²fe__2 r h,

⁼ ЬТс " (Ь + с) (l + 2fc)’

и так как ^t£=ch»?i, то

Tik

^е° ~ (1 +2fe)ch4i ’

Величину eh»?! обозначим через х_г, так что

T k

^е» ⁼ _Xl(l+-lh)

при этом х_г > 1 всегда, и можно пренебречь величиной 2 к по сравнению с 1, т.ч. Со⁼

Вследствие малости к и эксцентриситет в современных установках вообще незначителен, но в нек-рых искусственных опытах разность г_х-г₀преднамеренно делается большой и эксцентриситет становится сравнительно большим. Последствия этого теория сейчас же может указать. При сравнительно большом е₀ х_г становится близким к 1 (*! s 1 при е₀, мало отличающемся от к), но т. к. есть расстояние начала координат от центра подшипника, то это начало будет в таком случае близким к окружности под-шипника. Соответственно α= i sh j?_x=г_х Уx - 1 будет величиной малой, и оба полюса координат Неймана лягут вблизи окружности подшипника один вне ее, другой внутри. Тогда, если мы проследим изменение угла |, начиная от точки, где |=0(maximum толщины слоя смазки), то увидим, что £ будет весьма медленно изменяться на сравнительно очень большой части окружности подшипника и только при самом подходе к наиболее узкому месту слоя (где ξ=π) ξ будет быстро возрастать на очень небольшой части окружности. Т. о. главное изменение величины § будет происходить на малой дуге по обе стороны линии центров,

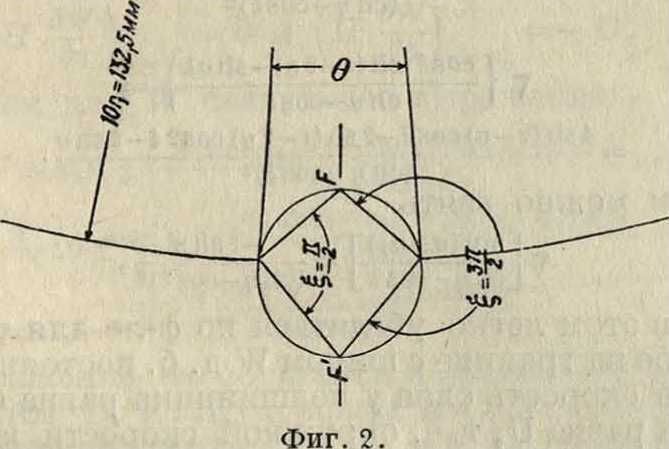
на всей же остальной части окружности подшипника изменение ξ будет незначительным. Но мы видели, что давление на подшипник м. б. представлено ф-лой р_х=В_х sin ξ + В._г cos I + В₃ sin 2 £ +

+ B₄cos2£ + B₅,

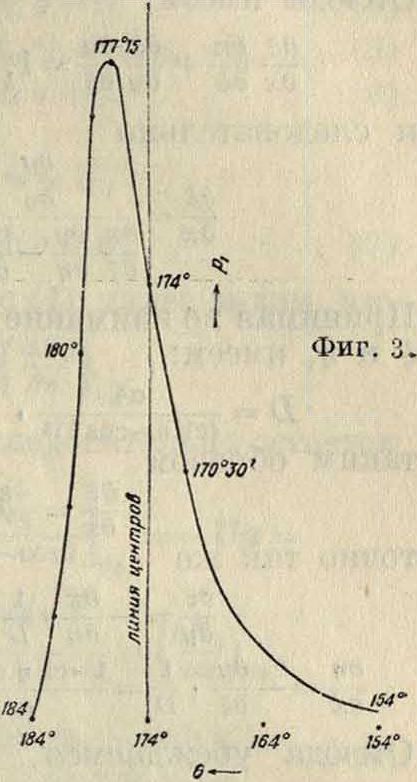
где Bi, В₂,.—постоянные, и следовательно давление будет мало меняться там, где мало меняется ξ, и наоборот,—очень быстро там, где сильно меняется ξ. Т. о. в рассматриваемом случае сравнительно большого эксцентриситета незначительная часть окружности подшипника будет участвовать в восприятии главного изменения давления, остальная же часть будет как бы нерабочей. Опасность такого распределения дав ления очевидна: смазочный слой в тонком месте м. б. вытеснен и начинается опасное сухое или полусухое трение, могущее повести к повышению температуры и горению масла. Подобное изменение угла £ представлено (фигура 2) в десятикратном увеличении и взято из опытов Стентона (Stanton), где в восприятии давления участвовал лишь слой небольшого протяжения (30 и 15°) и эксцентриситет был сравнительно велик (фигура 3).

С точки зрения гидро-динамич. теории смазки можно заранее сказать, что подобные опыты не имеют практич. значения. Более подробно с теоретич. стороны об этом будет сказано далее. Теперь же для детального выяснения величин B_lt В₂,. необходимо обратиться к т. н. ф-ии тока. Если скорости какой-нибудь точки жидкости по осям×и Y будут и и V, то ф-ия то—

_тх, dW д W

ка W определяется условиями и== — д^-·

На линии тока Ж=Const, и разность значений Ж для двух линий тока определяет количество жидкости, протекающее в единицу времени между двумя линиями тока. Действительно возьмем в жидкости какой-нибудь элемент ds (в положительную сторону координат) и обозначим через а и β косинусы углов, которые нормаль к этому элементу делает с осями координат. Тогда количество жидкости, протекающее в единицу времени через элемент ds, выразится через dip={аи + βν) ds; но ads=dy и -βάβ —=dx и следовательно

ΰψ i)W dw d W

ду ду дх дх

Соотношение для dip показывает, что там, где ψ (или Ж)=Const, через эту линию никакой жидкости не протекает, то есть это—линия тока, и с другой стороны,

2

Ψ2 — Ψ1 — f (^аи + βν) ds Ж₂ — Ж_х1

представляет количество жидкости, протекающее в единицу времени между двумя линиями тока. Т. к. ди dv

ду дх

ТО

d*W

= Δ W.

О 02 w

Ζ (ο z=-----i--

дх 2 ^ ду2

Переходим к координатам ξ,η. Имеем: ЭПК _d*W (Οξγ, d*W (ду * ~дх“~~№

, d*W dS

Но

par β*

ΛΟΙΤΤ Я1

+ 2 ЭПУ _ ЭЛУ

ду2 ^— эг vayj

¹ ~ dSdy ду ду ду“

dW дЧ. dW д“у, д$ду дх ¹ d.x^{a 1} ду йх^а

a*vy (д( ^г j_ any (Оуу

⁺ дуг дХУ дЧ ЭХУ д²у д£ дуг ¹ ду ду²

W /ду г η г дх ) 0W д ду д·.

d£=|| dx + ~dy dvj^ — dx + dy

Э£ ду ¹

ду ду и с другой стороны,

йх=Щ-df-hgf-	d»=$J
Отсюда имеем:
0{ дх 0i ду 1дх di + ду 0i	df дх, дх ду ‘
и следовательно ду
df δη	_ ду
дх дх ду дх ду ду

0у 04

άη.

0i ду _ /. 0! 04

1

X)

Of ду δη Of

Принимая во внимание выражения х и у через ξ V. η, имеем:

а²

ду _ -sh^sinf. eij ~ ^а Teh ч-cosi)² ’

(сКч-cos!)² таким образом

0i __ - sh ч sin I.

Од: а ’

точно так же

Of _ Ох i chy cosf-1. ду ~ δη

δη дх ’

ду Of

D

-cht? cpsf

О??

ду

shy sinf

(chi?-cosf)2 /d²W, д²ИЛ α² V Of а Ο»?² J

Отсюда убеждаемся, что

©²+©²=(l)^a+(S²=(cb.-cos^;

0ί 0Ч_, 0i 8η_ _ ₀ 0²i 0²£ _ 3²ч. 0²Ч __п

0х 0х ду ду ~ ¹ 0х^{2 1} 01/² ох² ду‘ ~

Следовательно W W _ ₂

0х² дуг ~ - “ α² V 0ί²

ИЛИ

0²W. 2 соя²

9i² “1" 0ч² ~ (сЬч-COSf)² ’

то есть ф-ия W должна удовлетворять условию V [(ch »7 — cos£)² уИП=0, т. к. у 2 со=0. Носо-гласно этому последнему соотношению 2ω является суммой произведений гиперболич. ф-ий на тригонометрические, и следовательно W вообще должен быть суммой таких выражений f, которые после составления суммы вторых производных от каждой и помножения на (ch η — cos f)² дают каждая какую-нибудь сумму произведений гиперболич. ф-ий на тригонометрические. Т. к. 2 со заключает по принятому выше 4 тригонометрии. ф-ии cosf, sini, cos2£, sin2f, то yf будет состоять из членов вида ^cb’^,cos~

Возьмем поэтому выражение операции у оно обратится в _(ch)J__cosi)aправилам диференциации имеем:

(eh»?-cosf)² 1.

ch??-cosf ⁵ ch η + COS f

ИТ.π. после, а по

Vfifz^-fiVh + hvfi + Z ( и, взяв f_x=будь f₂

0/1 0/а, 0/ι 0/2 Ί

Vfih

ch η — COS f 1

1 d 2

df df ¹ δη δη )

получим при каком-ни-

(ChiJ-COSf)

Jja [.(ch η — cos i) у +

+ f₂ (ch η + cos i) - 2 (sin ξ ^ + sh щ ^ J.

Отсюда, например при f₂=sin £, получаем _ sin £

^v cii4-cos{

Пользуясь этим и принимая=a /2=»7 — %> получим:

7-4l)Sinr]_ 2 Sini Sll4

cosi)² ’

sin.;

сЬч-cosi

,r(4-4i)sini1 _ 2 sine

¹ L сЬч-cosi J (сЬч-

точно так же убеждаемся, что г sh ч

Vic

.)

»-»r KETSSiji С^(ch ” - С) “Ь ’ +

+ sh η (ch η + cos ξ) — 2 sh η ch η ]=0; и далее

vG

I" (ч-ч i) sh ч I _ 2 [ch ч (ch ч - cos i) — sh² η ] ij~ (сЬч-¹

2 — 2 ch η COSf,

(сЬч-cosi)^{2 :}

(sini sh24 _ 4sh2 ч sin £ сЬч-cosiJ ^— сЬч-cosi _ 4с!г2ч sh4 sini _ 4sh4 sini-2sin2{ sh24 (сЬч-cosi)^{2 —} (сЬч-cosi)²

/sini СЬ2ч _4sinich4-2ch24 sin2i V ch4-cos{ ^— (сЬч-cosi)²

.сЬч-cosiJ (сЬч-cosi)²

_ 2 — 2chч cosi.

ИЛИ

Так же далее I cosi

η

СЬч-cosi)=(сЬч-cosi)² [ - (^ch 4 - COS i) COS i +

+ ^cos f (^ch 4 + cos i) + 2 sin² i ]=·

Следовательно

4sh24 cosi

/cosish24) _ 2sh2ч

V ch ч - cos i/~ (ch Ч-cosi)² ^ ch ч - eos i 4 COS i Sh4 ch24 4 COS i Sh4-2sh24 COS2 i

(сЬч-cosi)² T.o., выходя из выражения

(сЬч-cosi)² 1

ch4-cosi ’^получили целый ряд выражений, могущих по сказанному войти в выражение ф-ии тока. Но W подлежит определенным условиям на границах слоя. Можно принять по самому определению W=0 на окружности подшипника, то есть при η=η₁. Первые два выражения удовлетворяют этому, остальные нет. Поэтому мы возьмем в 3-ми 5-м выражениях вместо sh 2 η множителем sh (г — 2»)) — sh а, где τ=η₀ + η₁, а σ=η₀-η₁; этот множитель равен 0 при η=ηχ. Тогда получим

rsini[sh(T-24)-sina] > _

V ( сЬч-cosi —

_ 4sh(T-4)sinj-2sh(t-24)sin2£

(сЬч-cosi)²

И

f CQSi[Sh(r-24)-Shσ] 1 _

V I сЬч-cosi ^—

_4sh(r-4)C0Si-2sh (τ —24)C0S2j—2shff

(сЬч-cosi)²

Затем можно взять

. Г sin (ч ч ιΠ _ _ Lch4-cosiJ (

-2sh4

(сЬч-cosi)²

как в этом легко убедиться по формуле для y/i/₂. В слое на границе с шипом W должен быть постоянным, далее скорость слоя у подшипника равна 0, а у шипа равна U, то есть окружной скорости шипа. Скорость слоя в направлении окружности подшипника можно выразить через W сл. обр. Име-0W dw

ем -_д~=и, -g—=— v, возьмем на окружности подшипника какую-нибудь точку и через нее проведем две оси координат, из которых одна х будет радиусом, а другая у касательной. Т. к. ξ=Const—ур-иё какой-нибудь окружности,вмещающей угол ξ на данном отрезке 2а, то проведем через выбранную точку эту окружность, она пересечет окружность подшипника (η=Const), как уже было сказано, под прямым углом, и ось х будет к ней касательной, a у ее радиусом. Предположим, что мы выразили ф-шо тока в этих координатах, тогда

aw

ду т дх

Следовательно на окружности подшипника

dW „ dW dW Э£, dW ду

-5-7-=О, НО -_я, =17 77 + 7- ~а~*> ^{И так как 0СЬ} дх ’ дх di дх δη дх ⁷

X имеет с окружностью ξ=Const две общие бесконечно близкие точки, то 1^=0 и ⁰

дх ^w “ дх

dW δη

“"dS"·®?» ^но> ^с ДРУ^Г0Й стороны,

+ — -и. пе трудно видеть, что ~=-cos9,

ду ду _ду дх,

дх Ох дх’

a=— sin б, где б—угол оси×с осью×(ли нией центров). Выражаем cos £ через б: ь + с_п

cos б =

-COSS-7·

ь + с

2

раньше же было найдено:

rcosf ь + с

= г ch η, поэто му cos θ =

chijcosi-1

Подобным же образом

chi)—cosf

найдем sin б=— из выражения для у =

= г sin б через ξ к η. Теперь получим, приняв ду ду во внимание выражения для ”

И 77"—, ду’

ду _ (Ι-eh);cosS)^a + sh²4sm² f

дх

ch»)—cost

= H.

o(ch»j-cosi) a

Таким образом условие для слоя при подшипнике напишется

( Я=0.

V ду)_п=П1

Совершенно таким же путем найдем для слоя при поверхности шипа

(*?),-,.Г"·

где U—окружная скорость шипа. Следовательно W должно удовлетворять четырем граничным условиям:

ТЕ

^;0; -IF₄__4|1=Const =

4=4ι

где Q—количество протекающей жидкости в единицу времени в сторону вращения шипа,

^ =_0и(яа я ду ]„ =

П=У 1

ду )

= — U.

ч=4о

Возьмем для W следующее выражение:

^W=^sm S -chV-cosi ^h

+ A₃ (₄-_4l) + ^Αί5Μη-^ηΑ⁺±⁽Γ^ηι)^⁴ +

+

ch y—cosi A₆cosl[sh(r--2»))-sh r]

ch у - cos ξ

Выражение это обратится в значение для W, принятое Η. Е. Жуковским и С. А. Чаплыгиным, если положить А_х=А₃=0. Его можно написать также:

_{w =} lV_lsm_i±iV₂

сЬч-cosi ^ ³’

где N_x—множитель при sin ξ, а

N₃=Ai sh (η - η_χ) + Α₅ (η - η_χ) sh η +

+ A_e [sh (τ — 2 η) — sh <7] ch η и

Ν₃=Α₃(ί7 - η_χ) - Α₆ [sh (τ - 2η) - sh σ].

Первое граничное условие выполняется само по себе, второе требует, чтобы Ν_χ= 0, Ν₃=0 и Ν₃=Α₃σ + 2А_в sh σ=-Q, τ. e.

Α_χσ — 2Α₃ sh σ=0, (1)

Α_χ sh σ + Α₃ a sh η₀ + 2 А_й sh σ ch η„=0, (2)

A₃ а + 2A_a sh σ=— Q; (3)

далее третье дает то есть

(* ”)„=»·

А_х — 2A₃chn=0,

4* + А_ь sh η_χ — 2 А_е ch σ ch η_χ --

0,

четвертое

А₃ + 2 А₆ ch α= 0;

эщ

U,

А_х — 2 Дз ch σ=0,

(4)

(5)

(6)

(7>

это ур-ие тождественно с (4); далее видим, что

№ =	(дл-л
V ЗУ )ηι	ду )

Чо и нового ничего не дает, следовательно остается соотношение д

[о

ch)?— cos£)

ON.

04 ch»j-cos J_4o

δη

( ch η - COS £) - N₂ sh η

τ. e.

Cb.i7-COS!

1=№

^J4o 04 /40 ’

(8)

— Ua,— A₄ ch σ + Д₅ (sh % + a ch %) — 2 A₆ (ch η₀ ch σ + sh a sh η₀) =

= Λ ch σ + Π₅ (sh η₀ + σ ch %) - 2 A₆ ch (η₀ + σ).

Ур-ия (1) и (4) совместимы лишь при малых значениях σ, когда можно считать asish σ и ch σ= 1. Мы видели, что в современных установках величина σ всегда мала, поэтому с этим приближением мы и пойдем дальше. Ур-ия (1) и (4) дают А_х=2А₂. Далее вообще про граничные условия нужно сказать, что существенно необходимыми являются первые два, т. к. W должен быть постоянным на линиях тока. Вторые два условия—уже гипотезы, предполагающие, что смазочный слой на границах и у подшипника и у шипа имеет относительные скорости, равные нулю. Фактически эти условия могут и не выполняться. По ф-ии W мы найдем 2со, пользуясь данными соотношениями:

2 ωα²=sin ξ [-2 А_х sh η + 4Α_ζ sh (τ - ??)] +

+ cos ξ [—2 Α₅ ch η + 4 Α₆ sh (τ — η)] +

+ sin 2 ξ [-2 Α₃ sh (τ - 2 η)) +

+ cos 2ξ [-2 Α₆ sh (τ — 2 η)] +

+ 2A_s - 2Α₆ sh σ — 2 Μ₄ sh η_χ;

соответственно получим:

= sin ξ [-2 A₅shy-4A₆ ch (r - η)] +

+ cos ξ [2 A_x ch η + 4 A_z ch (τ — ?;)] +

+ sin 2 ξ [2 A₃ ch (t - 2)?)] +

+ cos 2 ξ [—2 A₃ ch (τ — 2 η)] + Const.

Положив здесь η=η_χ, найдем распределение давления по подшипнику согласно принятым граничным условиям. Определим коэф-ты Α_ά, Α_δ, А₆ из соотношений (2), (5), (8). Из (5) определяем М₄ через 4₅ и 4, и затем вставляем во (2) величину П₄, получим ур-ие

2 А_в sh a (ch a ch % — ch %) =

= А_ь (sh a sh η_χ — a sh %).

Но

ch η_α=ch (ηι + σ)=ch η_χ ch σ + sh η_χ sh σ; далее

sh %=(1 + ft) sh η_χ

и поэтому

σ (1 + k)-sh σ

2А_в=А_х

S№b

т. Э. т. XXIV.

27

Теперь получим

A_t=2Л₆ ch a ch η_χ - A_s sh η₁

т. e.

= A_S

A

choclun [g(l + fc)-sh g]-sh2ffshin sh²o ’

-sh(7Ch>Io + σ(1 + fe) Chach»)i ,

--iPi ^Л5‘

Подставляя теперь найденные величины в ур-ие (8), получим:

. ( - shdchoclujo + ^σ (1 + ft) [ch²och4i — ГсЬ(чо + о)]

А sh² а ⁺

sii б ch (чо+σ) + sh»gsh>io + gsh²gch4o 1 __ jj + Ь² σ I

Но а (1 + ft) [ch² <т ch ??! - ch щ ch а - sh η₀ sh а)== σ (1 + ft)[ -ch σ sh σ sh %- (1 + ft) sh %sh σ]== — а (1 + 7с) sh о sh η_ι (ch σ + 1 + ft);

далее

- sh σ ch σ ch η₀ + sh σ ch (η₀ + σ) + sh² σ sh %== 2 sh² σ sh η₀=2 (1 + ft) sh² a sh >h·

Таким образом

A {σ (1 + ft)² sh η_χ + в [(1 -f ft) sh ?h ch σ — ch η₀ shff] — 2(1 + ft)sh σ sh % j=Vasha и так как

(1 + ft) sh щ ch a - ch % sh a то окончательно

= sh η₁ И

Slli7

= Г,

затем

. _ _Ur_Isha

A ~~ <Γ+σ)ΐ + fc)²-2 (l + ft)sh σ’

₉ .___tfr. Го (1 +M ~Sha]

~A sha[<7 + <j(l + A²)-2(l + ft)Shn]

При малой σ получим: A=-g? и 2 А

Uri

ко

Uri ksh σ

Ur_xr_a

fteoshi)!

Теперь мы можем выразить распределение давления по подшипнику:

₌ _ 2№, ( W n,ChV| _ginμ ft V ft e₀sh»)i

+ 2Λ (ch 1?! + ch η₀) cos f +

Ur₀r 1

sin 2 I - A ch σ cos 2 f + B.

fte₀sh>!]

Вследствие малости разности η₀ - η_χ=σ можно приближенно принять ch % sch% и далее e₀ =

= _t o?=v sh² η_χ=(x - 1), затем пре небречь ft сравнительно с 1 и тогда получим:

- COS ξ --_ ^Х>Ь _r:=z sin 2 ξ —

Pi.

μ

r_xft²(xf-l) ¹ 4A_tXi

r²(x|-l)

Ai

r²(x²-l)

r_xft²(x²-l) J/x²-l COS 2 ξ +

r (scf-1)

Эта ф-ла, если положить А_хиВ=0, обратится в формулу Η. Е. Жуковского и С. А. Чаплыгина. Если выразим ξ через угол Θ, то получим I „ <ь—с) sine

(sin 1=2

+

Ух _	2U (
μ	№Τχ (oc| — 1) 4
4 А,хх j	r×COS0 + 1
r2(x2-l)	; COS Θ -f- Χχ ]
A,	(χ 24?
r (* -	• 1) (cos

•2r_x COS0 + Ь + С

(2 х -1)

и т

•^д·)’

sinft

COSfl + Xi

2x₁jJsin6(XiCOse + l) ft²n (xf-i) (cose + χι)² i)sin²e_x. В

Выведенное для p_x соотношение предполагает, как и вся теория, непрерывность смазочного слоя. На этом основании, если бы мы при исследовании опытных кривых распределения давления нашли в нек-рых случаях резкое противоречие с выводами из теоретич. ф-л, между тем как в других случаях этого противоречия не было, мы могли бы заключить, что в первых случаях при опытах не было непрерывности смазочного слоя. Представим себе, что имеется диаграмма распределения давления в ф-ии О, и отметим давления для Θ=- и θ=^ π, пусть они будут р_п и р₃₁, тогда получим по ф-ле:

у и. +

2 U

tAi

г1(х - О

ft^n (Xf — 1) * " ^1

2 U ,__Ajl_/х² —2 ___в г²(х²-1) X² i ^Т (х² — 1) ’

Xik²r_x

Ры_ 2 С

μ

(2x1-1)·^- +

А_х

х_х

(xf-2)

Κ*ϊ-ΐ)

4i,

Г²(х²-1)

В

+

Xl Xi Xj ’

и т. к. всегда х₁> 1

Фигура 4.

Xift²r_x(x²-1) ¹ г²(х²-1) х^{2 1} г²(х²-1)

Вычитая первое из второго, получаем:

Pii-Ри ft²ri(x|-l) 4(2x²-1) 4 8(х²-1) _

μ и ~ ^!

8 μυ

отсюда т,--г=х-

ft^2ri (P31-P11)

то должен быть

8μϋ > fcViiPj!- Рп)

или

8μΩ > к²(р₃₁-Ри),

где Ω—угловая скорость вращения шипа. Если это условие не соблюдается, то мы можем предполагать, что в опыте была нарушена непрерывность смазочного слоя, и следовательно имеем основание не принимать во внимание таких опытов. К сожалению линия центров, относительно которой идет вся ориентация, далеко не всегда по-называется в соответствующих опытах. Но в опытах Кингсбюри (Kingsbury) над подшипником с воздушной смазкой положение линии центров было определено длякаж-

дого числа оборотов при соответственном определении распределения давления по подшипнику. Фигура 4 и 5 показывают распределение давления для двух случаев при одной и той же нагрузке, но с чи об/м. 230 и 1730. Во втором случае кривая распределения давлений имеет правильный овальный вид, тогда как впервомонаиме-ет сильную впадину в месте минимума давлений. Нетрудно видеть, что в этом случае не соблюдается соотношение

8μΩ> ft²(p₃₁-Pu),

если мы возьмем ft=1 · 10^_3, μ=1,75 · 10^_6 кгм~² ск и соответствующие давления по диаграмме. Следовательно в этом случае существование

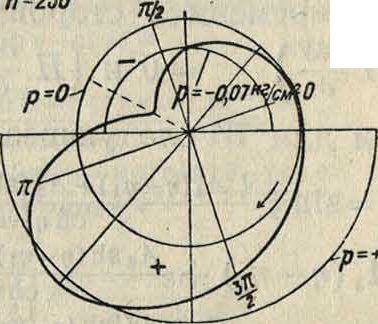
0,Икг/см^г

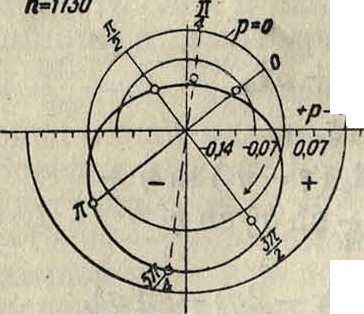
_}0,14нг/см“

Фигура 5.

ф-ии тока сомнительно, и опыт м. б. не принят во внимание. Этого можно было ожидать, т. к. воздушная смазка правильно функционирует лцшь при больших сравнительно числах оборотов. О второй кривой будет сказано дальше, а теперь перейдем к условиям внешнего равновесия. Определим тангенциальные и нормальные силы, действующие на слой, прилегающий к подшипнику. Если мы в точке на окружности подшипника опять проведем две оси×и У, радиус и касательную, то нормальная сила выразится (как было указано в общем введении) через ди

η=Ρι~

а тангенциальная

, ди, dv

^ί=-^1θ^+ e?)

ТТ dW

Но и=>-

ду

dW дх ³

то есть

dW

дх

0 и а по граничному ус-

* + v²=0,

предполагая х на

^=0, а,

ду ’ ’

окружности подшипника ф-ией у, имеем: d*W. d*W dx’ дхду ^r дх dy

-=0 (касательная) ^d*^w Ρ·

μ

и при ди дх‘

7=0

dx

dy

И П-

w=°’ ^τ· ^е-^г=

дхду

Аналогично получим ду дх

0, то есть

0²W

а так как 2 а>=~-

ду дх^у

ду·

ди ду

ТО t — 2μω.

Т. о. сумма сил реакции со стороны подшипника в проекции на ось Υ, то есть на линию, перпендикулярную к линии центров, найдется в выражении:

2 л

r_x I* (— ρχ sin Θ — 2 μω_χ cos Θ) άθ. о

При вычислении этой суммы встретятся инте-

2π 2л гралы

J sin ξ sin θ άθ, J·sin ξ cos θ άθ и т. д. Лег ко видеть, что

J sin ξ cos θ άθ=0.

В самом деле переменная часть в подинтегральной величине сводится к 0 άθ. Но если мы представим окружность разделенной линией центров и осью Υ на четыре квадранта, то каждый подобный член в первом квадранте имеет себе равный, но противоположный по знаку в четвертом квадранте, то же самое имеет место и в других двух квадрантах, и следовательно сумма их, то есть интеграл, равна 0. Подобным образом убеждаемся, что и

2 л 2 л

j‘ cos ξ sin θ άθ=0, J sin 2| cos θ άθ=0,

J* cos 2 ξ sin θ άθ=0,

и остаются следовательно интегралы

2π 2π

f sin ξ sin θ άθ, J sin 21 sin θ άθ,

J* cos I cos 0 άθ, J cos 2 f соs0d0. о · о

Для первого интеграла имеем, положив cos θ=ζ

π	+1
с sin2 e de	C (l-z2)dz
J cosO + x,	J (Z + 0C!)·/!-Z2
0	-1
	-fl +1
p (l-x2)dz	- г + c	Λ’ι dz
J (z + x1>Y 1 —z2	J V 1 —z2 J	V l-z2
-1	-i -1

j га *?) ₊„-i/"(“,

I ^aictgy ST

-1) (1-г)

+1) (1 + z)

+ 1 _ +1

— j Υί — ^ + x₁ J arc sin г=— (2]/a² — l) * + -1 -1

+ х_гп=я (ж, — Yx — l) и таким образом о

J sin ξ sin 0 d0 =2я (ж, — ]/a^ — l) Yx - 1.

о

Точно так же найдем

2π 2π

Г COS ξ COS θ άθ=Γ (X|Ms9±l)cosed9 _

J J cose+^j

-j-

+ cos6-XiSin²6 cosd + xi

2л

άθ:

= 2 я — ж, Г -5HL²i^ =

COS9+X,

2n

= 2 я (1 - x + ж, Υχΐ -1)=J sin ξ sin 0 άθ.

_ 0 Далее

άθ-

J sin 2 | sin θ άθ=2 J/ж² - ΐ j

_ 21/ж² — 1 Г ^sinefoiCose + i) _ c (x₁cos-:8 + cos8)de т ¹ L cose + x, J cose + x, J

sin² (jcxCosQ-i- 1) (COS0+.2Ci)²

_ о l/^i--Г Г Sin β (X, cos e + 1)

^{_ Xl} ~ ¹ L Μβθ + χ,--

- f άθ + 2x_t f -^s-^in2m 1

J ¹J cose+x, J

и в пределах получим:

2 Yx - 1.2 π [— 1 + 2 a?! (a?i — Vif-l)] =

= 4 π — 1 (ж, - -Ί)²·

Точно так же

Jcos 2 ξ cos 0 άθ=J (1 - 2sin²!) cos 0d0=sin0-

f₀. „ c 2(x²-l)sin²9cos0de

— J 2 sin²!cos 0 Й0=sm0 — J

, sin 0 -, 0(3* _ П f T°^s^.

cose+Xj + ~-^ж1 ^L) J cose + x,

(C0se+X,)2

de

X,

Первые два члена в пределах пропадают, третий равен

/9 _ 1-1 Г (2cos²e-i) de

^ ‘ ^J J cose + x, ’

и, заменяя опять cos 0 через г, убеждаемся, произведя интеграцию по вышеуказанному способу, что

2л

J cos 2 ! cos 0 άθ =4 π j/ж² — 1 (ж, — — l)².

о

Таким образом проекция на ось Y выразится:

2л

^ (2А₃ sh. ν_Λ + 4JL₆ ch η₀) J sin ξ sin 0 dd -о

2л

— 2A₆ ch о j sin 2ξ sin 0 dd +

о

9л

+ ^ (2A₃ ch η_χ - 4A₆ sh η₀) J cos ξ cos 0 d0 +

0

2 л

+ ^ 2^4₆ sh σ J cos 2f cos 0 άθ 0

и так как

2π 2π

j sin I sin 0 dd=j Co’s f cos 0^0 — о о

= 2π sh η_χ (ch η_χ — sh η{) и

2π 2π

J sin 2f sin Θ dO=J cos 2f cos Θ d0=о о

= 4π sh. (ch % — sh i?!)², то выражение проекции будет:

²”?^₅·2π sh П

члены лее с А₆ сократятся, т. к. они дают 2 · 4π · А_е sh гц (ch ί?_χ — sh η_χ) [ch r/₀ — sh η₀ +

+ (sh σ — ch σ) (ch — sh η,)], и, написав

ch η_α=ch σ ch % + sh σ sh η_Ιи

— sh J?j=— sh % ch a — sh a ch η_χ, убеждаемся в справедливости сказанного. Поэтому имеем в проекции на ось Υ, приняв во внимание, что

^AS=JST “ a²=rfsh²?b —= Psin в_и

№ f xl -1

где Р—нагрузка на шип и 0_х—угол ее направления с линией центров. При Θ_ι=-| получим ф-лу Η. Е. Жуковского и С. А. Чаплыгина (при малых fc² и σ).

Второе условие внешнего равновесия получим в проекции сил на линию центров. От реакции - р_х получим в проекции:

2π

— ^х— Г cos ξ cos 9 d0 =

Γι(χ|-1) J

2π ]/ж² — 1 (x_L — l) =

ΊΑιΧχμ

ri(xl-l)

_ ΙΑιΧ! 2πμ{χ_ι-]/xf -ΐ)

Α-ιμ

Γι(Χι-Ι)

n Vxl -i

2 л

J cos 2ξ cos 0 άθ -

ο

Αχ in μ

(Xl -У%1-1)²·

Γι Vxi-t

Оба слагаемых вместе дают--·

Далее в реакции 2«»!« имеем множителем (смотрите общее выражение 2соа²) при sin ξ выражение

£ (2Λ sh iji - 4Д₂ sh η₀)=-‘% кА_х sh щ-

Следовательно получим слагаемое в проекции и второе слагаемое

2 μΑζ Sh а-г а²

— J sin 2ξ8Ϊηθ άθ ·-

_ Αχ ·Τχ sh σ 4π ]/χ| -1 (эе_ж—"j/sef -l)² а²

И Т. К.

sh σ=— Sh η,

го ¹

kr,

Γ₀Χ₁(1 + 2/ί)

то второе слагаемое будет

^4π,Λι4ζι-]/5[

sh i?! s ^ sh %,

i)²;

Г1Х1

оба вместе дадут

_ ΙπμΙίΑχ (χ| — ]/«; -i) Ух“

riX,

В виду малости к сравнительно с 1 всем этим выражением можно пренебречь, тогда

ΊπμΑχ

“r7j7*rr^Pcos0-

Т. о. в двух уравнениях равновесия имеются три величины, подлежащие определению: 0_b ау (или эксцентриситет) и A_lt и следовательно нужен ряд опытов, могущих дать еще одно соотношение, например для угла Θ, или же ряд надлежащих опытов по распределению давления на подшипник. Нек-рая неопределенность теоретич. ф-л произошла потому, что здесь была выбрана ф-ия тока в наиболее простой форме, но эта неопределенность, с другой стороны, позволяет приблизить теоретич. ф-лы к результатам опытов. Теория все равно не может здесь охватить всего явления, т. к. предполагает зависимость в двух измерениях, между тем как на самом деле зависимость трехмерная. Опытов по определению угла 0_г в зависимости от. различных факторов мы пока не имеем. Лишь Кингсбюри в опытах с воздушной смазкой определял изменение угла θ_χ от скорости.

Обратимся теперь вновь к ф-лам распределения давления по подшипнику. На основании условий внешнего равновесия можем нап-исать л _ ^riU ctgfl,

^Λι~ да и теоретич. формула распределения давления будет

Ρχ __?_U_ sin0

^μ ίΛι(χ?-1)

Cose + Xj

ixiU ctgflj · (X!COs8 + 1) fXiUsin 0(xi eos0 +1)

ii²r₁(x?-l) · (cos e+x_t) ft²r₁(xj-l)(c0se + x₁)^a , Uctg9i Η _ 2 (xj — l)sin²6~[ _i_ β ^Гй²г₁(а;?_ 1) I. (cos 0.+ Xi)² J

или

μΩ

k4xl-t)

(Xl COS 8 + 1)

Pi

- 4x_t ctg 0_X

+ Ctg 0! [l

I (-4a:²

-2);

sinO

COS0 + X! 2XiSin0(X_lCOS0+l)

COS0-1-X! ^τ (cos0 + Xi)² 2 (x²-l)sin²0l

(COS0 + X,)²"]

В

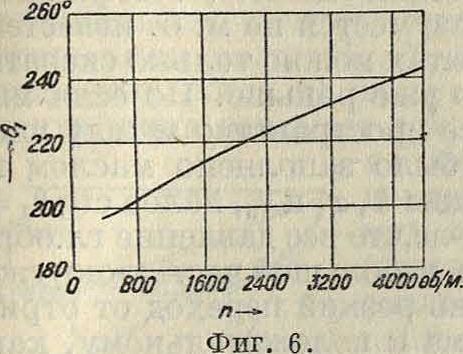
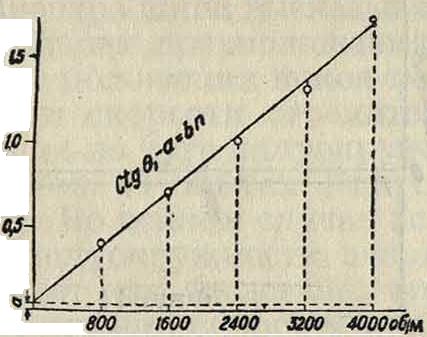
. Рассмотрим второй опыт Кингсбюри, где число оборотов шипа было равно 1730 в минуту. На фигуре 6 дана по Кингсбюри диаграмма зависимости угла 0_Х от скорости вращения шипа. Если сообразно этой диаграмме отложить на ординатах ctg0₁₍ а на абсциссах числа оборотов или угловую скорость (фигура 7), то можно принять, как показывает фигура 7, линейную зависимость ctg в_г от угловой скорости при одной и той же нагрузке. Будет ли угол зависеть и от величины нагрузки и будет ли подобная зависимость при постоянной нагрузке и в других смазывающих средах, мы за отсутствием опытов сказать не можем. В рассматриваемом случае для п=1 730 соответственно диаграмме можно принять ctg Θ₁=0,74; далее имеем μ=1,76 ·

• 10~⁶ кгм°ск, дляау примем величину 1,9. Тогда получим, приняв 7с=1 · 10~³,

μΩ

1,76 · 10 ⁶ -181,17

10-е.2,61

= 122,17 килограмм/м

Т. к. в приложенной диаграмме (фигура 5) распределения давлений масштаб давлений дает приблизительно 6,5 миллиметров=ОД кг /см², то 1 миллиметров=155 килограмм/м²; сообразно с этим были определены по формуле (при Л=0) давления в точках, соответствующих углам Θ=0, у, π, j, и отмечены кружками. Только одна шестая точка удаляется от опытного значения, остальные пять хорошо совпадают с опытными. Несовпадение шестой точки м. б. легко объяснено следующим образом: при движении (здесь по стрелке ча- %-сов) воздух как сре- & да сжимаемая, идя к | зазору из области с меньшим давлением, может преждевременно нагреваться, чем и повысится его Фигура 7.

давление сравнительно с тем, какое имела бы среда несжимаемая, теория же рассматривает среду несжимаемую. Поэтому мы можем сказать, что опытом Кингс-бюри вполне подтверждается теоретич. формула распределения давлений, т. к. получается хорошее совпадение как частных величин давлений, так и самого характера распределения их: и максимум и минимум давлений получаются по формуле именно там, где указывает опыт.

Если теперь мы обратимся к опытам с масляной смазкой, то встретимся здесь с большими затруднениями. Во-первых, отрицательные давления, то есть давления, направленные от подшипника, не м. б. здесь измерены со стороны подшипника, подсасывающее же их действие заставляет входить окружающий воздух внутрь смазывающего слоя. Тогда получается сложная смазывающая среда, коэф. вязкости которой неизвестен и меняется от одного места к другому в зависимости от примеси воздуха. Поэтому мы вправе ожидать, что 1) в таких опытах отрицательные давления или вообще отсутствуют или измеряются величинами, б. или м. удаленными от теоретических, и 2) в положительной части давлений м. б. также значительные отступления от теоретич. величин вследствие случайной примеси воздуха, которая может повести даже к разрыву масляного слоя. Об этом см. замеч. Bradford’a в Trans. A. S. Μ. Е. 1931. В пояснение сказанного возьмем опыт Гюмбеля (Giim-

bel). В этом опыте к сожалению не были приняты во внимание все требования теории и не был определен ни эксцентриситет ни угол линии центров с линией действия нагрузки. Диаграмма распределения давлений дана на фигуре 8 (кривая а), из которой видно, что небольшие отрицательные давления были наблюдаемы на небольшом протяжении, на остальной же части окружности давления были положительные, что и следовало ожидать, т. к. воздух имел свободный доступ в пространство между шипом и подшипником, к-рый в сущности был муфтой, надетой на вал, подверженный действию груза, и удерживаемой неподвижно. Коэф. к в этом опыте можно принять на основании данных размеров г и г_х равным приблизительна 0,02. При такой большой величине к возможен и большой сравнительно эксцентриситет, а следовательно х_г может иметь значение, близкое к Г.

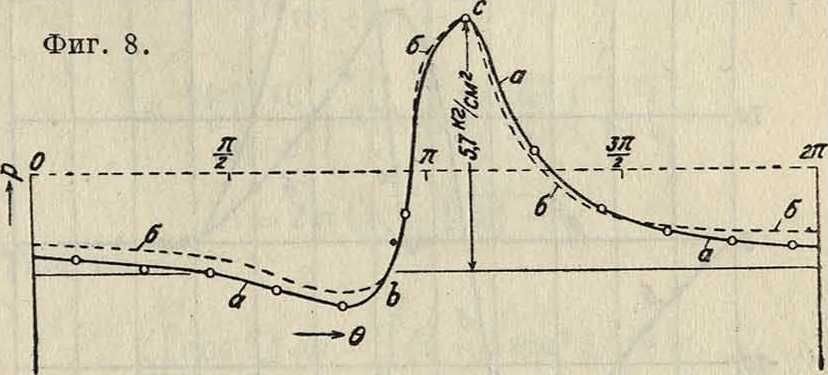
Мы возьмем здесь ж₁=1,14 и ctg6₁=l. Тогда вычисляем по формуле давления для различных точек и, построив теоретич. кривую б, совмещаем точку с наибольшего давления с соответственной точкой опытной кривой, чем и определим постоянное В. Сравнение кривых указывает и в этом случае хорошее согласие опытной и теоретич. кривой, насколько это можно было ожидать от опыта, произведенного не вполне по указаниям теории. Характер обеих кривых одинаков, на участке Ьс обе кривые почти совпадают, только в теоретич. кривой давление в общем несколько равномернее распределено, нежели в опытной, что после сказанного понятно само собою. Т. о. и в опыте Гюмбеля мы имеем подтверждение правильности теоретич. решения вопроса. Далее мы можем взять кривую, приведенную Бредфордом (Bradford) и названную им типичной кривой распределения давлений (в дискуссиях по поводу опытов Кинг-сбюри). В этом случае, как видно из фигура 9, мы имеем величину эксцентриситета и угол линий центров 0j, к-рый здесь равен 37,5°. По coin h о.оозо, г“

отношению —=-=(^в нашем случае) берем пробно к=0,0034, коэф. вязкости такой же, как и у Гюмбеля, далее согласно Bradford’y п=500 и полагаем х_г — 1,4. Во всех подобных случаях, когда неизвестен закон зависимости угла 0! от скорости и нагрузки, чем и определялась бы величина х_ь приходится разумеется идти путем проб. Мы получаем т. о. по подстановке частных величин в общую формулу кривую распределения давлений, которая представляет хорошую копию (фигура 10а) с кривой Бредфорда а, если отбросить часть с большими отрицательными давлениями. Между тем именно по поводу этой кривой Бредфорд говорит о разногласии между опытом и теорией, приведя на фигуре 9 (кривая б) теоретич. кривую Гарисона (Harrison). На это можно только сказать, что теория Гарисона является неполной, теория же Η. Е. Жуковского и С. А. Чаплыгина, несколько здесь расширенная, дает типы кривых распределе-

ния давлений, вполне сходные с опытными. Далее Бредфорд приводит в общих чертах данные другого опыта, где по возможности было устранено втекание наружного воздуха в пространство, занятое смазкой. В этом случае угол линий центров с линией действия нагрузки

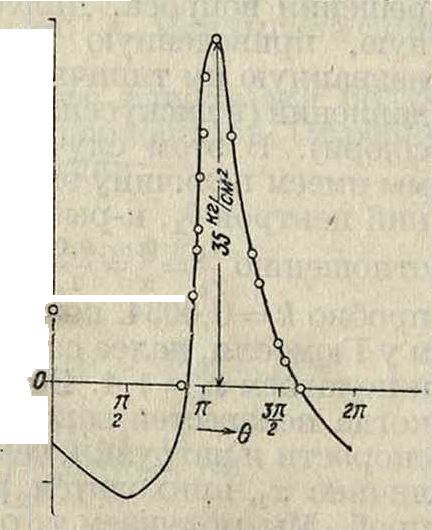
увеличился на 12°, эксцентриситет уменьшился на 10%, возросло измеренное отрицательное давление, а также длина дуги, над которой давление было положительным, т. ч. согласие с кривой Гарисона стало лучшим. Принимая во внимание прежнюю величину 7с, мы должны взять согласно новому эксцентриситету х=1,6 и при ctg 0_{1 =} 0,854 вычисляем по формуле относительные величины давлений, т. к. величина максимального давления не дана. Получаем кривую (фигура 106), которая действительно лучше под-ходит к кривой Гари- да сона, нежели прежняя опытная. Отсюда можно заключить, что дан - ^го~

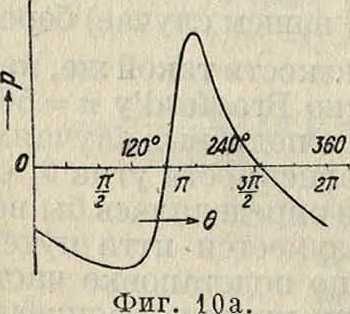
ная здесь формула распределения давлений дает полный отчет об опытах, произведенных при самых различных условиях.

. Обратимся вновь к опытам, описанным у Стентона в его книге «Friction», где масляный слой ограничивался дугой в 30° (1-й опыт) и в 15° (2-й опыт) и где эксцентриситет был очень большой; во втором случае он равен 0,7488 миллиметров при г₀=12,5 и к имело не встречающуюся теперь в установках величину 0,06; величина х_х в

этом случае близка к 1 и равна 1,0015. Смазочный слой по всей окружности состоял следовательно из небольшой масляной смазки и большой воздушной, в которой вероятно плавали капли масла, увлекаемые шипом. Коэф. вязкости такой среды разумеется не м. б. известен и поэтому об этих опытах можно только сказать то, что было сказано уже раньше. Но если мы предположим, что все пространство между шипом и подшипником было заполнено маслом и возьмем те же величины к, х_х и е₀, далее ctg 0_Х== 1, то убедимся по ф-ле,что все давление гл.обр. воспринимается лишь небольшой частыоокруж-ности, где будет очень резкий переход от отрицательного максимума к положительному, как это показано на фигуре 11. Кривая давлений, если мы отбросим отрицательные давления и начало счета давлений положим на линии, соединяющей крайние точки диаграммы в направлении счета градусов, весьма хорошо подходит по характеру к обеим кривым Стентона. Отсюда мы можем сделать следующие выводы: 1) т. к. величина х_х определяется при данных Ω, μ и к из ф-лы равновесия по величине Р (считаем 0_Хтакже зависящим от Ω и μ), то величина х_хвыходит близкой к 1 при значительном Р, и эта перегрузка, как и следовало ожидать, ведет к нерациональному распределению давлений, могущему вызвать разрыв смазочного слоя и

	трение уже сухих поверхностей, хо-1 тя бы все про- странство -между шипом и подшип- ником казалось залитым маслом;
f у	—в ψ
ФПГ. Н. 1

2) неточность обработки шипа и подшипника, вызывающая увеличение коэф-та 7с, также ведет при данных Ω, μ и Р к уменьшению величины х_хи следовательно к той же опасности разрыва. Поэтому точность пригонки диаметров шипа и подшипника есть первое необходимое условие для рациональной смазки при значительных Р, и нельзя допускать,чтобы величина /сбыла больше 0,005. Но вообще величина х_х зависит и от скорости при данных μ, к и Р; влияние скорости на величину х_х мы можем однако вывести лишь из опытов Кингсбюри с воздушной смазкой. Как было указано, там можно принять линейную зависимость ctg 0_Х от скорости шипа; далее было найдено, что для п=1 730 метров б. принято х_х — 1,9; при этом получается хорошее согласие в распределении давлений с опытными данными. Если скорость п=1 730 назовем через й₀, а какую-нибудь другую через Ω_χ, то по формуле равновесия при данных к и Р получим следующее соотношение

^βι V _ sin е_1Х

где х₁₀ и sin0{_o относятся к Ω₀, а х_п и sin 0_U—· к Ω_χ. Подставляя сюда sin0_x по диаграмме зависимости θ_χ от скорости, получаем величины х_х для различных скоростей, выходя из х_г=1,9 для и=1 730. Сообразно этим значениям ж_хможем определить соответствующие эксцентриситеты по формуле е₀=—. Тогда получим диа-

об/мин л =800

2400

3200

4000

Фигура 12.

грамму движения центра шипа при увеличении числа оборотов (фигура 12). Предполагается, что нагрузка действует по линии 00 и из точки О проведены лучи, дающие положение линии центров; согласно диаграмме на них отложены величины эксцентриситетов в значительно извращенном масштабе. Т. о. можно представить движение шипа по следующей схеме: в покое центр шипа занимает самое нижнее положение _с на линии нагрузки и эксцентриситет имеет максимум х_х=1. При вращении (здесь по стрелке часов) смазка увлекает шип, и центр его сначала приближается к горизонтальной линии (если линию нагрузки считать за вертикаль). Эта часть пути центра шипа не показана на чертеже, т. к. соответственных опытов не имеется. При дальнейшем увеличении скорости вращения (начальное п=800 об.) центр шипа движется по некоторой кривой, постепенно приближаясь к центру подшипника, и при скорости бесконечно большой оба центра должны совпадать. Т. о. при увеличении скорости вращения постепенно уменьшается эксцентриситет, увеличивается Χχ и распределение нагрузки становится все равномернее. О движении центра шипа высказывались различные произвольные предположения, например, что центр шипа из положения покоя постепенно при увеличении скорости стремится к центру подшипника, идя по дуге полуокружности в сторону вращения. В опытах Кингс-бюри мы этого не видим. Во всяком случае гипотеза о движении по полуокружности вверх к центру подшипника дает как следствие, что линия центров при увеличении скорости приближается к горизонтали, между тем опыты Кингсбюри дают как-раз обратное. Но за недостатком надлежащих опытов с масляной смазкой вопрос пока не имеет решения. Можно только предполагать по аналогии с воздушной смазкой, что при выходе центра шипа из состояния покоя трение до достижения известной скорости является смешанным, то есть отчасти сухим, отчасти со смазкой. К этому состоянию гидро-динамич. теория приложена быть не может и следовательно необходимы тщательные опыты для характеристики этого состояния.

Перейдем теперь к определению по теории момента пары, препятствующей вращению шипа. Момент пары, стремящейся повернуть подшипник, будет

2л

М=J 2μω_χ r (W — Ре₀ sin в_1г

о где Р—нагрузка на шип и е₀—эксцентриситет; равная ей и противоположная пара является парой сопротивления. При вычислении интеграла нужно принять во внимание, что

2 я

sin I άθ=0. Это можем видеть непосредст-

S

венно, разделив окружность на четыре квадранта и приняв во внимание, что первый и четвертый квадранты, равно как второй и третий, взаимно уничтожаются. Точно так же и

2л 2л

J*sin 2ξ άθ=0, и остаются интегралы Jcos £ clQ о о

2л и J cos 2ξ άθ.

о Но

Гсов I άθ=Г άθ=- Г Ш— ·= =

J ^Ь J cose + Χχ J Χχ+Ζ У Χ-_Ζ2

₌_ г χχάζ, г

J уΧ-_Ζϊ ^τ J (*! +ζ) Υι-ζ-

и следовательно

2π л +1

Γ 3CJCOS0 + 1 Γ XlCOSjbfl _rlq_o f ^χι^__

J cosfl + *i COS6 + *! ^aa ~J νΪΖΪΪ

0

-1

+ 1

-²J

(x|-l) dz

J (*1 + z)Yu^i +i

= 2πΧχ

"Ь

2(χξ-1) I, I /*Xi-1 1-2

i rn

= 2я(хх-

Так же

2π 2π

J"cos 2 ξ άθ=J*(l — 2 sin² ξ) άθ ·

СП

= 2^-2(ж²-1) J

= 2 π —

i 2(xJ-i)sin0

j| COS0 + X1 0

sin² Odd (COS0 + Xi)²

2 n

+ 2 x - 1) f

cos θ άθ

COS0 + Xj

2n

= 2 π + 2 (x - 1) f

COS Sde COS0 +.Xi

+1

= 2 π + 4 (a?J — 1) J

zdz

J (*! + Z) Vl-Z*

+1

= 2 л + dz

так:

prj

a²

(Xi +z) /l-2²]

= 2 π + 4ηΥχ* — 1 {Υχϊ^Λ-Χχ).

2 л

Т. о. в общем виде J 2 μ<θχΤ άθ представится

О

2 л

% Г( - 2 А_ъ ch % 4- 4 А_в shy₀) f cos ξ άθ -^L о

2л

— 2 А_е sh a J cos 2 ξ άθ + 4 π (Η₅ — ο

— Α_β sh σ - Αχ sh %) j;

подставляя значение Αχ через А₅иА_в, получим:

2 л

{(- 2А_ь ch ηχ + 4 А₆ sh η₀) f cos s άθ -^ 0

2л

— 2 Α_β she J cos2£d6 + 4л[А_ъсЬ? τ,χ-о

- Α₆ (sh σ + 2 ch σ ch ηχ sh ηχ)]},

но sh η₀=sh η_χ ch σ -f sh σ ch η_ι и поэтому при A_t коэф-том будет выражение:

2л

4 ch σ sh v_tl J* cos ξ dO -f o

2л 2л

T-sha^cin^ j cosfd0 —2 j cos2|d0 — 4π j. ό о

Здесь множитель при sh а равен

4x_t · Ζπ(χ₁ — У х — l)— 4π —

— 8πΥχ — 1 — 1 — Ti) — 4 π=О,

следовательно:

2 ²⁷¹ —J- |Г 2 А₅ ^2 π ch² η_χ — ch η_χ J cos ξ dO^j -f

о

2л

+ 4A₆cha sh η₁ ( J* COS ξ dO — 2 π ch 7?^ J=о

= ν^ί-ϊ - 2 Λ ch a(xf - 1)J =

= sh »?! (Α_δ ch η_χ - 2 Λ ch σ ch η_χ),

и т. к. а²=rf sh² то

2л

J г^си^² <20=^ (A ch η_χ - 2 A ch σ sh η_χ).

Далее, т. к. Р sin 0_t=⁴*^/ri^_t°^Sh’^?1 (_см выше) или Рsinв_х=У?У и е«-^г°*^bа

, то Ре₀ sin =

гiShijt “ ⁰ sh»/i

1πμΓ₀Λ, Stlcr×πμΑ _Β sh σ 4 πμΑ_τ> Sh σ

Поэтому

r₁sh²t;_l

sh²>)i(l + ft) shijish^o

HO

J 2μα>_xrl άθ — Pe₀ sin θ_χ=Μ =

= ё |> (^ch - йПй) - Ach σ sh _4l],

chtj^hno-shCtjo-T)!) _ <Λΐ)₀sini, shi)o shj;₀

И

Μ=4(Α|^-2Α<Λσ)=

_/<„„77« j Ch»?oSha

- 4 π,м ur_x [o + ad + feja-^i + fejsh^sh,, ~

_ [σ (1 + ft)-Sho]cho 1

Shn[o + n(l + ft)2-2(l + ft)sh<ji г

Приведя к одному знаменателю, получим в числителе выражение:

ch η₀ sh² σ — σ (1 + ft) ch a sh η₀ + sh σ ch σ sh η₀== sh a [ch η₀ sh σ — a (1 + ft)² cth σ sh η₁ +

+ ch σ (1 + ft) sh η_χ]=sh σ [ch j?₀ sh σ —

— sh ch σ — σ (1 + ft)² cth σ sh % +

+ 2 (1 + ft) ch о sh %]=sh a sh jj_x [- 1 - σ (1 +

+ ft)² cth σ + 2 (1 + ft) ch σ], следовательно

M =

4πμΤιΙΙ σ(1 + ft)2cthcr-2 (1 + ft) Chff + 1

1+ft σ+ a (1 + ft ) a — 2 < 1 + ft) Sho

Принимая теперь, как и везде, σ малой величиной, получаем

М=— ^ίπμϋτ4 Далее можно взять

sha=?i-sh»?₁

(i+ft)sho r_thyx*-i

и поэтому

__X^πμUtqхi(l + 2ft).

ft (1+ ft) У ж²-1

можно взять как абсолютную величину момента пары сопротивления выражение а коэф. трения

h ~У зс²-

М,_ ¹ Рт₀

4πμϋΧι

PhV xl~i

если принять. во внимание выражение Р через U, х_1} к и sin бц то можно также написать λ=х_хк sin 0_t

или

λ=^т—~ sin 0_Х.

«о ¹

Величина потерянной на трение работы выразится по общим правилам через

±πμϋ*Χι (1 + 2fc)

L =

ft (1+ it) У x -

или просто

πμυ*Χ

= Ρϋλ.

ft У x*-l

Τ. к. всегда ®ι>1, то дробь

Χι

будет тем

У х -

ближе к 1, чем больше х_г, то есть чем меньше эксцентриситет, и потеря в работе на трение при данных U и к будет тем меньше, чем больше ж_х, что понятно само по себе. В выражение коэф-та трения входит в знаменатель Р, то есть нагрузка на единицу длины. Теория предполагает для каждого сечения, перпендикулярного к оси пары шип—подшипник, одинаковое распределение давления на подшипник, то есть независимость всего явления от измерения вдоль оси. В действительности это предположение б. или м. не соблюдается; распределение нагрузки по оси может иметь разнообразный характер, и отсюда может получиться несогласие между тео-ретич. коэф-том трения и наблюденным, хотя бы для распределения давления на подшипник в центральной его части и получалась хорошая согласованность между теорией и наблюдением. На фигуре 13а и 136 показаны два распределения нагрузки по длине I /—1— подшипника: одно по опы-

А 1	λ	/ГЛ
		,У Ί; V.
		1-1-4
Фиг.	13а.	Фигура 136.

r₉3C,( 1 + ift)

там (Тоуера) с масляной смазкой (фигура 13а), другое по опытам Кингсбюри с воздушной смазкой (фигура 136). В последнем случае, если вычислим среднее давление на единицу длины, мы получим его почти вдвое меньшим, чем в центральной части, между тем теоретически мы его предполагаем одинаковым и равным давлению в центральной части. В случае же Тоуера распределение нагрузки ближе подходит к теоретич. предположению. Предположим здесь величину х_х сравнительно большой,

J-7T—— можно считать близким к 1, и

V _х -у поэтому к=Const=*^Лру тогда или, при постоянном μ, — ss Const, то есть при определенной скорости U величина А будет обратно пропорциональна Р. В опытах Тоуера это до известной степени оправдывается, как показывает табл. 1.

Таблица 1.—3 начения Л в зависимости от Р.

Р, atra	Ω=15,7	β=36,6	Ω=47,1
36,6	8-10-1	14-10-4	17-10-4
21,8	15	23	27
7	45	77	89

Т. о. теоретич. вывод находит здесь себе подтверждение. Но в опытах Штрибека соотношение это совсем не подтверждается. Тем не менее и опыты Штрибека, с другой стороны, указывают на правильность теории. Действительно, если предположить, что опыты произведены при одной и той же нагрузке, но с разными скоростями, и т. о. исключить вопрос о распределении нагрузки по длине подшипника,‘то по формуле мы получим, что коэф. А будет возрастать приблизительно пропорционально скоростям. Фигура 14 дает изменение коэф-та А в опытах

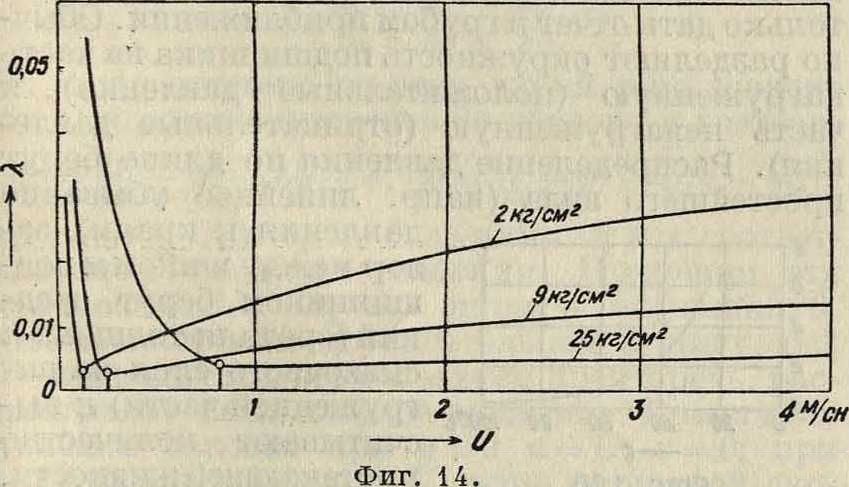
Штрибека в зависимости от скорости. Сначала коэф. падает—эту область можно отнести к полусухому трению; затем, пройдя известный минимум, он правильно почти по прямой поднимается, причем правильность увеличивается с увеличением нагрузки, что и должен быть по теории. О разнице между отдельными значениями А по теории и по опытам Штрибека определенного ничего сказать нельзя, т. к. им не был определен коэф. к. При этом последний в опытах должен был меняться, хотя опыты и производились на определенном подшипнике, именно вследствие того, что для изменения коэф-та вязкости менялась t°, при изменении же t° коэф. к по причине разности в коэф-тах расширения шипа и подшипника изменяется. На это обычно не обращают внимания, между тем это имеет значение, особенно при тщательно приработанных шипе и подшипнике, где коэф. к< 0,002.

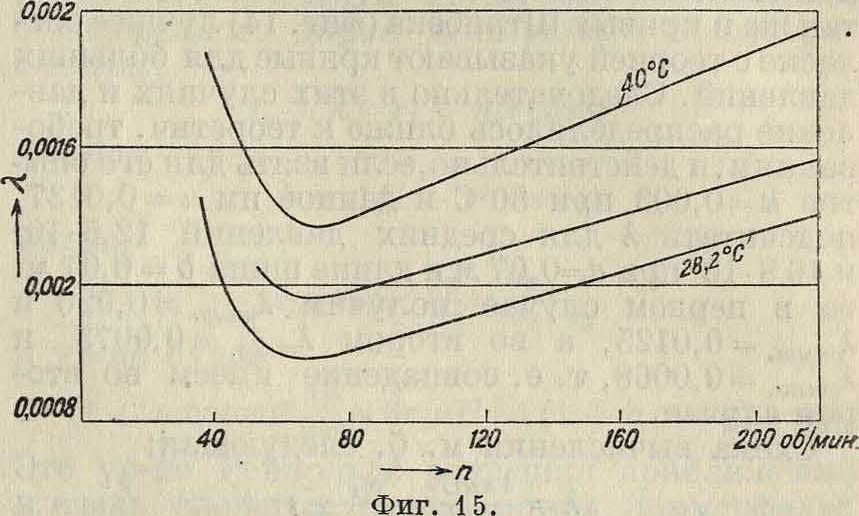
Подобным же недостатком страдают и опыты Бюхе. Здесь для получения одного и того же коэф-та вязкости различные масла нагревались до разных Г и затем определялся коэф. А при одной и той же нагрузке и разных скоростях. Фигура 15 опять показывает такой же характер изменения А, какой дает ф-ла, но отдельные величины разнятся несмотря на одну и ту же вязкость. При этом мы не имеем сведений ни о характере распределения давления по оси ни о коэф-те к, к-рый в виду особенно тщательной здесь пригонки несомненно для различных t° имел и различные значения. Поэтому ничего нельзя сказать о правильности объяснения этой наблюденной разности в значениях А влиянием т. н. адсорбции, то есть известного сгущения (или разрежения), производимого частицами метал

ла в смежном масляном слое. Из опытов Штрибека Гюмбель выводит соотношение, которым часто пользуются, именно

^Al^//^^=Const·

Так как

А=xje sin 0J,

^т0 fc=—

Χχ&ΐηθχ

и следовательно

4_:πμυχ*5ΐηΘ₁ру х -1

или

А

л Г Р 1 /X i sin ^θι

у 4 _πμυ у у-

Полагать правую часть равенства постоянной, как делает Гюмбель, нет никаких оснований. Это значило бы (если мы возьмем х_г сравнительно большим), что Χχ sin θ₁=Const, т. e. λ —=Const, чего разумеется ни в опытах Штрибека. ни в других опытах нет. Поэтому соотношение Гюмбеля произвольно.

Мы видим из всего сказанного, что теория налагает известные требования, которым должны удовлетворять опыты, если они желают вполне осветить сложный вопрос о трении со смазкой. Эти требования следующие: 1) при всяком опыте должен быть известен коэф. к и, если опыты происходят при разных Г, должно заранее определить зависимость к от темп-р; 2) при установившемся числе оборотов должен быть определено направление линии центров и эксцентриситет или толщина слоя в самом узком месте; 3) должен быть определена зависимость угла линии центров с линией нагрузки от угловой скорости шипа, от коэф-та вязкости и возможно от величины нагрузки;

4) должен быть обеспечена однородность смазочной среды и для масляной среды устранена возможность втекания наружного воздуха; 5) при каждом опыте должен быть сохраняема постоянная ί°; 6) размеры коэф-та к должны подходить к размерам в существующих хороших установках; 7) в каждом опыте должен быть определено распределение нагрузки по длине шипа. Тогда можно будет выяснить, какие поправочные коэф-ты должен быть введены в теоретич. ф-лы, т. к. ни одна теория не может охватить явления во всей его сложности. Заметим, что определение коэф-та трения или потерянной на трение работы дает уже при сравнении с теоретич. ф-лой в общих чертах понятие а распределении нагрузки по длине, например в опы-

•тах Тоуера приближенно соблюдается, как мы видели, теоретич. соотношение для коэф-тов трения в зависимости от скорости; наряду с этим и распределение нагрузки по длине до известной степени подходит к теоретическому. Точно так же в кривых Штрибека (фигура 14) лучшее согласие с теорией указывают кривые для больших давлений. Следовательно в этих случаях и давление распределялось ближе к теоретич. требованиям; и действительно,если взять для его опытов fc=0,003 при 30°С и данное им ,«=0,0137, подсчитать А для средних давлений 12,5-10⁴ и 46,8-10’ при d=0,07 метров и длине шипа Ь=0,07 м, то в первом случае получим l_mmv.=0,026 и 1_0)шт.=0,0125, а во втором=0,0073 и пыт.=0,0068, то есть совпадение имеем во втором случае.

Схема вычисления м. б. следующая:

ίπμΧΙ X!

А =

Рк

, ίπμυ

«отсюда А > ~_pj~

4 ημΙΙ 2

ТГ)

Vxi-i

Здесь Р (на единицу длины)== 46,8-10⁴d= 46,8 · 10’ · 0,07, 17(1100 об/мин.)= — 4 м/ск, следовательно

. 16л-137-10“4

^λ> 16,8-104-0,07 -3-10-3 ’

то есть А >0,007. Но, с другой стороны, как будет указано дальше,

А < |/" к²

«г. е.

А < ]/9 10“» + 49 · ЮЛ или А < 0,0076. Отсюда имеем удовлетворительное совпадение •с опытной величиной. Но разумеется эти теоретич. числа гадательны, т. к. неизвестно действительное к. Не нужно думать, что только при •очень длинном шипе действительность будет приближаться к теории. Наоборот, при длин-’ном шипе возможно скорее его прогибание, и тогда распределение давления будет значительно отступать от теоретич., тогда как в недефор-мированном и коротком оно м. б. гораздо ближе .к теории. Затем из соотношений для А можем получить следующее: т. к.

А=xji sin 0-.= - ^1лУ^хУ-_:,

Pky х²-1

то, исключив х_и имеем:

А² — к² sin²=(iff)²

sin*

θι=[Α²-

(ίπμυγ-, 1

V Рк I J ft» ’

1 /4ллУ 2

⁺ feaI Pk ) ’

e.

W><¹ +

- пВbт (t — t_a) -

pj_t _ ,-

«откуда U > у A² — /с². Если U этому соотношению не удовлетворяет, то будет Т. н. полусухое трение, всегда ведущее к изнашиванию поверхностей шипа и подшипника. Т. о. при жидком трении к всегда меньше А. Потерянная на трение работа и при жидком трении идет на нагревание, и можно приближённо написать рц>.

427 ’

здесь Ώ—диам. шипа, b—его длина, т—коэф. теплопередачи от подшипника в наружную среду. Если ввести Р_т=-~,то получим т =₄.

Здесь даны результаты опытов Стентона над изменением А от ί°, в зависимости от чего изменяется и коэф. теплопередачи т (фигура 16а). Кривая А_х дана для подшипника с нагрузкой

0.004

от

0,001

М

	V
у,
		ч	к.
		</77 т,

50 10 90 ПО !30°С

Фигура 16 а.

175 кз/см² при Ώ=50,8 миллиметров, Ь =57,15 миллиметров и п==1 300 об/мин. Кривая А₂ для того же подшипника с нагрузкой, равной 35 кз/см², при той же скорости шипа.

Внизу даны сравнительные величины и ж₂, а на фигуре 166—диаграмма коэфициентов ,« для соответствующего масла в зависи- а мости от 1°;при этом 7 ^ш коэф. дан в физич. | единицах, и его нужно помножить на 0,0102 для перехода на кг ск/м~².

Кривые т₁ и т₂ даны в предположении ί° наружной среды в 20°; из них видно, что ж падает с повышением ί° и стремится к независимости от нагрузки. Насколько однако это заключение м. б. общим, могут показать лишь тщательные опыты.

Относительно убыли смазывающего тела вследствие вытекания по краям шипа можно только дать отчет в грубом приближении. Обычно разделяют окружность подшипника на часть нагруженную (положительные давления) и часть ненагруженную (отрицательные давления). Распределение давления по длине берут простейшего вида (например линейное убывание давления к краям), зазор между шипом и подшипником берут средний (средняя толщина h смазочного слоя на на20 μ бо~~вГ1оо°с груженной части) и вы-

_считывают количество

Фигура 1бб. протекающей жидкости,

как в трубе прямоугольного сечения с высотой h и шириной, равной части окружности, имеющей положительные давления (например ¹/_а). Известная формула движения вязкой жидкости дает в этом случае объём у _ 1 0,25яс?₀ (di —do)³P ^V “ 12 Jdx ’

2 p

где p можно считать=2 p_m =, l=j-b, d_l и

d₀—диаметры подшипника и шипа Ηχ=3,45— нек-рый коэф. по Фальцу, к-рому принадлежит этот способ. Точно так же и на части с отрицательными давлениями

У 1 O,15nd₀p₀(di-do)^

¹’ 12 μΐχ1

где Ро—давление, под которым подается масло, а χ₁=1,74 по Фальцу. Расход слагается из

суммы этих величин. Про этот способ можно только сказать, что он прост. По существу же здесь теоретически сложная задача, и т. к. характер распределения давления по длине зависит даже от той или иной конструкции подшипника, то в общем виде эта задача и не разрешима без каких-либо б. или м. произвольных предположений. Практически она имеет лишь малое значение, т. к. вообще подача масла бывает с избытком в конструкциях хороших типов. О теории Мичеля относительно плоского трения и трения в пятах см. Пяты.

В заключение статьи уместным является рассмотреть в общих чертах, к каким результатам пришли после Рейнольдса исследовате-

ли, шедшие по намеченному им пути. Рейнольдс исходил разумеется также из общих ур-ий вязкой жидкости, то есть

ш=^“’ %=%=μ η

и

Эи, Эг> 9w _ л дх ду dz ’

В применении он принимает, что имеются две плоскости с относительным движением. Плоскости м. б. параллельными или иметь относи- · тельный небольшой наклон. Если вместо плоскостей будут кривые поверхности, то по его мнению кривизной поверхностей можно пренебречь, т. к. радиусы кривизны вообще велики сравнительно, с толщиной смазывающего слоя. Пусть ось×направлена по относительному движению, ось Y перпендикулярна к плоскостям или поверхностям и ось Z перпендикулярна к оси×по поверхности; далее принимается: υ (скорость по У) мала сравнительно с и и w, изменения и и w в направлении×и Z малы сравнительно с изменениями по оси У. Тогда для движения внутри смазывающего слоя получим ур-ия др _ д“и др _ ~ др _ 92_W,

дх ^ ду² ’ ду ’ dz ^ ду² ’

^ _ ди. ду. dw ^U “ дх~^~ ду ~т~ dz *

Т. к. по второму из этих ур-ий р не зависит от у, то молено получить из первого и третьего

1 .<>, г., _. др 1

др -

U — ~~ — V^й дх 2μ ^J

by-

b_гу где b, с и b₁ и βχ м. б. ф-иями жиг соответственно граничным условиям. Применим эти соотношения к случаю шипа и подшипника. Ось×направим по касательной к шипу, ось У—по радиусу и осью Ζ можем пренебречь, рассматривая лишь плоское движение. Граничные условия таковы: при у=0 u=U, г>=0; при у — h и=0, V=0, где U равно окружной скорости шипа и h—расстояние в направлении У между поверхностями шипа и подшипника; это расстояние есть функция аз. Отсюда определяем:

и

h ’

я т. о.

1 др 2μ дх

(χ-*)ν + ϋ(ψ)-

Условие несжимаемости дает ~ ~=0 и сле довательно

Интегрируя по у, получаем:

и на основании граничных условий с_{1 =} 0 и 0=—

дx 6μ дх) дх

Отсюда

= βμΙΙΙι + Const.

Постоянное определим, назвав через щину слоя при р=тах. Там ^=0 и Const—— 6μΟ7ι₀. Т. о. получаем:

(*“*·)·

Переходим к полярным координатам. Пусть радиус, проведенный из центра шипа к какой-

К тол-поэтому нибудь точке подшипника, образует угол φ с линией центров (длина этого вектора равна Io + h) соединим эту же точку с центром подшипника и назовем эксцентриситет через ηΔ, где /1=г₁-г₀и»<1. Тогда получим из тр-ка, образованного двумя векторами и эксцентриситетом:

r₀+ h=r₁ + ηΔ cos φ.

Отсюда

h=Δ (1 + n cos φ),

потом аз=Τ₀φ,

др дх др 1 ’ д<р г₀⁹

и ур-ие оудет

Δ³ (1 -f n cos φ)³= 6r₀yU [Δ (1 + n cos φ) — h₀].

Это ур-ие Рейнольдс разрешил приближенно в очень сложных рядах, потом Зоммерфельд упростил его формулы и наконец Duffing 20 лет спустя после Зоммерфельда (1924 год) дал интеграцию его при помощи подстановки где у—новое переменное. Рассмотрим общий смысл этой подстановки. Предположим, что эксцентриситет очень мал, т. ч. можно без большой погрешности положить φ^θ, где в— угол, который делает радиус подшипника г_ипроведенный в рассматриваемую точку, с линией центров. Тогда вспомним, что

(5 +с) COSΘ +27*1 2r₁cosO- -b + с ⁹

если мы опять возьмем систему координат Неймана. Отсюда

cos ξ=-

= V

Ь + С - 2Γχ b+C + 2

* ¹⁹

^2 =

"I /^~¹⁺ b + c, f 1 /~^{ί +} χι. ξ b +c Xi

и из приближенного выражения эксцентриситета, данного выше, можем написать жх rife _г Δ_ —

¹ г₀

Поэтому

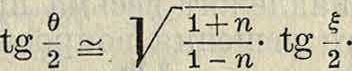
Мы видим отсюда, что преобразование Duffing’а есть скрытый переход к системе координат Неймана.· Но с этого и нужно было начинать и тогда решение всего вопроса было бы поставлено на надлежащую почву. Ур-ие Duffing’a для распределения давления по подшипнику имеет такую структуру:

С sin η — Ώ sin 2η·

Оно напоминает первоначальную формулу Жуковского и Чаплыгина, но присутствие аргумента η в первой степени указывает на то, что основное ур-ие Рейнольдса не представляет движения жидкости между двумя криволинейными поверхностями. Можно поэтому не говорить больше о формуле Duffing’a.

Более осязательные результаты получены от метода Рейнольдса в области трения плоских поверхностей. Мичелю удалось даже решить вопрос в некоторых частных предположениях в трех измерениях. Представим себе опять две плоскости с масляным слоем между ними, нижняя пусть совпадает с плоскостью ZOX, верхняя имеет размеры: по оси Z— b и по оси X—а. Возьмем, как и выше, ур-ия для и и w. Для и, как и раньше, ур-ие будет

^дрh)y + U ΰΡΑΔ·

u=4~ 7Г (у

2μ дх

ДЛЯ W ЛОВИЙ

получим на основании граничных ус-

i др, ₇ V

^w=ltiTz(y-V У,

если принять, что для у — 0 и y=h скорости по оси Z не существует. Подставляя значения да _ а-w _в у_СЛ0ВИ8 несжимаемости, определяя

dv

dz

—, интегрируя по у и принимая во внимание, что V=0 для у=0 и у=Ь, получим

„ dh _ д /h² др, 9 I др

^ bх~bх брдх ) ”1" Θζ δζ

Верхняя плоскость принимается слегка наклонной к нижней (угол Θ); рассматривая распределение давления в слое в данный момент, мы можем всегда взять оси координат так, что h=x sin θ — хс. Но, пренебрегая координатой z, мы имеем ур-ие:

dx дх 6μ дх)

Положим, что мы определили отсюда р в ф-ии х, и назовем его через р₂. Тогда, вычитая это ур-ие из предыдущего, получаем

(*·??).

где р₂=р — Pi, причем р_х—ф-ия только х. Положив здес h=cx, получим:

з др₂, е“р₂ __nara

-I-

дх^{2 т} х дх

Примем p₂=f(x)fi(z), тогда получаем т ш)+J ш ш+«*) f =о.

Если возьмем f(z) такой, что m²f₁(z)=fl(z), то получим обыкновенное диференциальное ур-ие

dx²

причем очевидно /i(«) =

ch mz

Это диференци-

sh mz

альное ур-ие решается в Бесселевых ф-иях и ведет к весьма сложным вычислениям. Но Duffing’y принадлежит весьма простой способ приближенного решения вопроса. Он пренеб-

3

регает средним членом - ~~ в основном ур-ии, то есть, другими словами, в ур-ии

О-*;(*£) + £(»£)

пренебрегает малым наклоном плоскостей, считая h — Const. Тогда для р₂ получим ур-ие:

д²р₂, д²р₂ _ „ дх² ‘ dz2 ^υ·

Примем, что подвижная пластинка симметрично расположена относительно плоскости ΥΟΧ, так что в направлении оси Ζ имеет измерения i b; примем также симметричное относительно средней линии пластинки распределение давления, тогда для р₂ получим:

, ch mz (с sin тх + о cos тх).

X —— Xq и×——

Ρζ=ΣΑ,

Граничные условия р₂=О при=х₀+ α= х₂. Поэтому имеем: sin тх₀, cos тх₀ sin тх₂, cosm®₂

О

sin т (х₀— х₂) =— sin та.

Отсюда т=—, где п-

Pi-

ηπζ.

- ΣΛ„ ch — sin

^п a

целое число, и т. о. пл(х-х₀)

Потом граничное условие р=0 при z=± b дает р₂=— Pi при z=i b, поэтому

— Pj=ΣΑ_η ch — sin

Имеем и следовательно нужно определить h°^=Qp^u(h-h₀), положив h=cx и h₀=cx₁, получим но Pi=0 при ж=гс₀ и х=х₀ + α= х₂; отсюда 2^₀ + а) _{Const =} i,

¹ с (2х₀ + а) 2х₀ + а то есть

_ W 7 1, ,т₀ (хр + а) ,__ί_

"! с² I х ^т (х₀ + а)х² 2х„ + а)

Теперь поступаем так: взявши измерения пластинок b и а, вычерчиваем диаграмму р₂ и представляем pi рядом Фурье. Для определения коэф-тов ряда имеем известное соотношение:

А_п ch ^=² Г - _Pl sin dx.

^п a a ,J _с

При этом интеграл легко м. б. определен графически при известных нам значениях р₂. Достаточным при этом оказывается взять небольшое число членов ряда (4—6). Таким путем определим коэф-ты А_п, потом получим р=£ _Ап (ch ψ - ch ^п-£) sin ·

Суммарное давление будет т₀+а ь

Р=2 j* dx J р dz =

хо о

= 2α!ιΣ — · (1 — cos ηπ) (sh _ ch —^.

Сопротивление скольжению на единицу поверхности равно

/du. dv ди _ U др h

^ dy ‘ дх) ~~ Р cil//2/=о ^ h дх 2

Полное сопротивление выразится

x₀-fct b

R=Zf _αχΙμ(£-ψ_χ )άΖ =

Χο+α b

2 bpU

²f v£^bdx-2f Jf_xjdxdz-

x₀ о

b x„+a x₀+a

^a-²f[ I (f p)4f vclx^dz-

ln

OC₀Xq -f-

0 x₀

. ZbpU j_n x₀ -

3Co

4- - P ^ 2 ’

так как вставка по граничным условиям пропадает. Коэфициент трения дается отноше-

R

нием ~р _л Н. Мерцалов.

Сухое трение. Шероховатости, пыль, вода, смазка и прочие, находящиеся на взаимно скользящих поверхностях, обусловливают возникновение сопротивления скольжению, называемого силой трения. Для чистых сухих поверхностей при отсутствии воздушной смазки в довольно широких пределах изменения скоростей и удельных давлений сила трения подчиняется закону Кулона,к-рый состоит в следующем:

1) сила трения пропорциональна нормальному усилию между поверхностями, 2) не зависит от величины соприкасающихся поверхностей, то есть от величины удельного давления, 3) не зависит от скорости скольжения, 4) зависит от материала и состояния поверхностей. Коэф. пропорциональности между силой трения Т и нормальным давлением N носит название коэф. трения (/), следовательно Т =fN. Различное физич. состояние трущихся поверхностей вызывает однако отступления от закона Кулона, которые состоят в следующем. 1) В начальный момент движения коэф. трения покоя (f₀) в 1,5—2 раза больше коэф. трения движения. Таблица 2иллюстрирует^-

фигура 17 для чугуна по чугуну при р=2,9 к г/см². Чем больше уд. давление, тем большей скорости соответствует минимум коэф. трения. Поэтому в сильных колодочных тормозах, работающих в области влево от минимума, сила трения будет тем больше, чем меньше скорость скольжения

" 10 20 20 40 10 60 70^си/си

Фигура 17.

колодок по ободу колеса и самих колес по рельсам. 4) При тщательной обработке трущихся поверхностей при соприкосновении их прояв-

Т а б л. 2.—Коэфициенты трения скольжения.

	Покоя			Движения
Материалы		Смочено
	Сухо		смазано	Сухо	Смочено	смазано
Дуб по дубу, волокна ||..	0,62	_	0,11	0,48		0,075
» » » торцами..	0,51	0,71	—	0,34	—	—
» » » волокна i ..	0,43	—	—	0,19	—	—
Бронза по дубу.. Чугун по дубу..	0,62	—	—	0,24—0,21	•—	—
	—	0,55	—	0,5—0,3	0,22	0,1
Коша по дубу	0,6—0,5	—	—	0,5—0,3	—	—
» » чугуну ..	—	0,38	0,28	0,56	0,36	—
Дерево по металлу..	0,6	0,65	0,11	0,40	0,24	0,10
Сталь по стали ..	0,15	—	0,12—0,11	1 0,09 при ν= 3 м/ск 0,03 при υ=27 м/ск
Сталь по фосфористой бронзе
1) плоские поверхности..	0,11	—	0,098	0,105	—	0,032
2) цилиндрич. поверхности..	0,169	—	0,16—0,13	0,162	—	0,15—0,1
Сталь по сварочному железу.	0,13	—	0,11	—	—	0,10—0,08
Сталь по чугуну ..	0,33	-	-	J 0,27 При V= 2,2 М/СК 1 0,13 при v= 20 м/ск
Чугун по чугуну ..	—	—	0,16	—	0,31	0,10—0,08
Чугун по сварочному железу.	0,19	—	—	0,18—0,17	—	0,08—0,07 0,08—0,07
Чугун по бронзе..	—	; —	—	0,20—0,5	—
Бронза по бронзе.. вый канат			0,11	0,20	0,10	0,06
1) по необработ. дереву..	0,5	—	—	—	—	—
2) по полированному дереву. Каменная кладка	0,33
по камню	0,5—0,7 0,42-0,19	—	—	—	—	—
» железу		—	—	—	—	—
»дереву	0,46—0,60	—	—	—	—	—
» бетону	0,76	—	—	—	—	—
» растит.земле..		сухой 0,6э, сырой и глинистой			0,30
Сталь по льду	0,027			0,014

величину коэфициентов f₀uf для различных материалов при различном состоянии поверхностей. 2) С возрастанием уд. давления коэфициент трения увеличивается. Это отступление подтверждается табл. 3.

Таблица 3.—3 ависимость коэфициента трения от давления.

Удельное давление, кг/см2	* 1	*2	*3	*4
8,79	0,110	0,174	0,166	0,157
13,08	0,250	0,275	0,300	0,225
15,75	0,271	0,292	0,333	0,219
20,95	0,297	0,329	0,344	0,211
25,22	0,350	0,351	0,351	0,206
31,51	0,395	0,365	0,351	0,208
36.77	0, Ю9	0,366	0,357	0,223
44,58	*5	0,367	0,367	0,235
49,92	—	0,434	*5	0,231
57,65	—	*5	—	0,273

** Сварочное железо по сварочному железу. *2 Чугун по сварочному железу. *з Сталь по чугуну. *.* Бронза по стали. *5 Поверхности повреждены.

3) При постоянстве давления имеет место минимум коэф. трения, зависящий от скорости

V. Этот минимум представлен на диаграмме ляются сцепляющие молекулярные силы, значительно бблыние, нежели вызываемые атмосферным давлением силы трения. Это отступление обнаруживается на точных калибрах-плитках Иогансона, к-рые, бу-

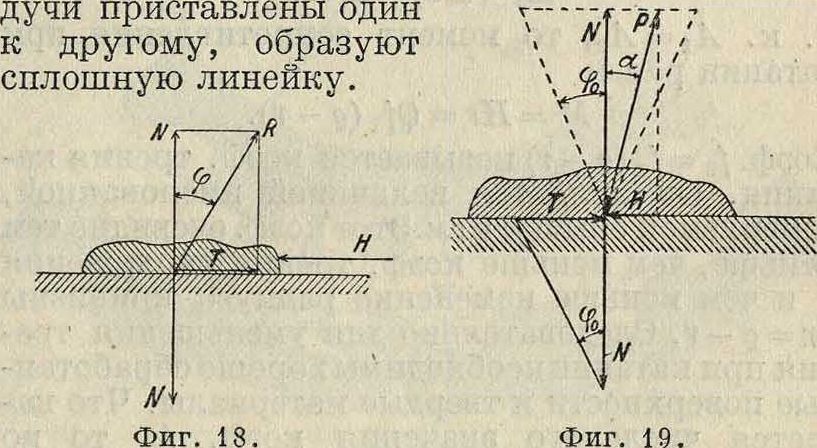
Если представить коэф. трения в виде тангенса нек-рого угла φ (фигура 18), называемого углом трения, то есть положить f=tg<p, то T=Ntg<p.

Из этого соотношения следует, что: 1) равнодействующая нормального давления и силы трения, действующих на движущееся тело, отклоняется от нормали на угол трения φ, 2) тело не сможет выйти из состояния покоя независимо от величины внешней силы Р, если последняя приложена к телу под углом а к нормали, меньшим <р₀. В этом случае (фигура 19) очевидно, что движущая сила Н меньше силы трения Т, т. к.

Н=Р cos α= N tg а < N tg φ₀.

Здесь имеет место явление самоторможения, которым широко пользуются в машиностроении— в болтовых и клиновых соединениях, в домкратах, в червячных грузоподъемных блоках. Конус с углом при вершине 2<р₀, описанный вокруг нормали к поверхности скольжения, называется конусом трения.

Стремление к устранению непостоянства коэф. трения скольжения и его вредного действия вызывает замену трения скольжения (первого рода) трением катания (второго рода). Эта замена повела к изобретению и многообразному конструированию шариковых и роликовых подшипников (смотрите). Сопротивление катанию зависит от деформации соприкасающихся поверхностей им. б. приведено также к силам трения скольжения. Эта мысль, высказанная Рейнольдсом, элементарно приводит к следующей анали-тич. зависимости. Предположим, что шарик или ролик находится под нагрузкой Q и что вследствие деформаций, не выходящих за предел упругости, радиус кривизны г его опорной поверхности увеличивается до величины ρ, которая остается постоянной за все время перекатывания (фигура 20). Если шарик повернулся на угол а, то путь, пройденный центром его, равен Sr=га. Но т. к. действительным радиусом качения является ρ, то при отсутствии скольжения путь центра шарика должен бы равняться s₂=ga. Следовательно путь скольжения шарика s₂-s₁=(e-r)a.

Называя коэф. скольжения между поверхностями через fi, находим силу трения по .Кулону Т=ОД и работу трения

А=Qfi (Sa - «i)=Qfi (Ρ -Г) a. Горизонтальная сила Н, производящая перекатывание шарика, совершает за это же время работу

А₂=-HSj=Наг.

Т. к. А₁=А₂, то момент сопротивления при катании равен

M=Hr= Qf₁ (ρ — тонн).

Коэф. /₂=fi (ρ — г) называется коэф. трения катания. Он является величиной именованной, измеряемой обычно в см. Этот коэф. очевидно тем меньше, чем меньше коэф. трения скольжения f₁ и чем меньше изменение радиуса кривизны Дг=ρ — г. Следовательно для уменьшения трения при катаниинеобходимыхорошо обработанные поверхности и твердые материалы. Что касается числового значения коэф. /₂. то по опытам Штрибека он уменьшается с возрастанием нагрузки и очень мало меняется с увеличением числа оборотов. Предельные значения, полученные им при испытании двух однорядных шариковых элементов для вала диам. 70 миллиметров с диаметром шариков d=7/8", даны в таблице 4. На фигуре 21 представлены кривые изменения коэф. трения катания по опытам Симансьюго (Германия). Кривая а относится к однорядному

Таблица 4.—Зависимость коэфициента тре-ни я катания от нагрузки и числа об/мин.

Нагрузка, кг	при 65 об/мин.	при 780 об/мин.
380	0,0033	0,0037
3 000	0,0015	0,0013

шариковому элементу, кривая б—к двухряд-ному. По диаграмме видно, что при некоторой нагрузке имеет место минимум коэф. трения катания и что однорядный шарикоподшипник выгоднее двухрядного.

Смазка шарикового подшипника не уменьшает коэф. трения катания, наоборот, густые и вязкие масла способствуют увеличению сопротивления катанию. Если шариковые кроликовые подшипники смазываются, то гл. обр. для того, чтобы предупредить образование ржавчины и поддерживать весь шариковый элемент в чистом отполированном виде. При работе шариков во влажном и пыльном воздухе употребляются смазочные мази, которыми следует полностью, но не плотно заполнить весь подшипник. При сравнении подшипников шариковых с подшипниками скользящего трения можно отметить следующие преимущества первых: 1) уменьшение вредного сопротивления, 2) трение при пуске в ход и в работе почти постоянно, 3) меньший расход смазочных материалов, 4) меньшие размеры подшипника,

5) чистота и легкость ухода.

Трение в машинах. Для уменьшения работы трения шипа по подшипнику поверхности их подвергают смазке. Смазочное масло (смотрите) долж-но иметь вязкость (смотрите), отвечающую давлению, числу оборотов и темн-рным условиям работы подшипника. Вкладыши подшипника должен быть пришабрены к шипу, т. к. весь успех смазки зависит от относительного зазора к=между >

подшипником (диам. 2г_х) и шипом (диам. 2г₀). В первый период вращения шипа имеет место приработка его к подшипнику, что сопровождается сухим трением вследствие наличия неровностей на соприкасающихся поверхностях. При этом шип несколько приподнимается, накатываясь на поверхность подшип-ника(вправо при вращении по часовой стрелке). Затем с возрастанием числа оборотов наступает период полужидкостного трения— поверхности соприкасаютсялишь своими неровностями, в углубления которых проникает смазка. Движение вала приобретает дрожащий и неустойчивый характер. Масло, увлекаемое шипом, отделяет его наконец от подшипника, и между ними сохраняется при установившемся движении смазочная пленка. Наступает период жидкостного трения. Центр шипа смещается при этом влево. С возрастанием числа оборотов при постоянстве всех прочих условий центр шипа перемещается по некоторой кривой, стремясь к совпадению с центром подшипника при п— со. На фигуре 22 кривая а представляет (в μ) боковые перемещения центра шипа, кривая б—вертикальные. По ним построена траектория центра шипа—кривая в Кривые относятся к шипу и=65 миллиметров, 1=250 миллиметров при удельном давлении р₀=1 килограмм/см² и при керосиновой смазке; на фигуре 23 даны кривые для того же

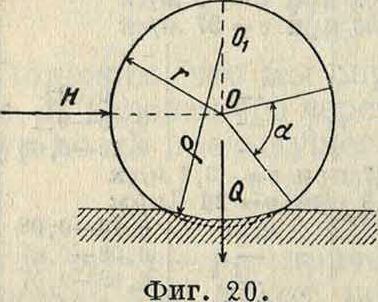
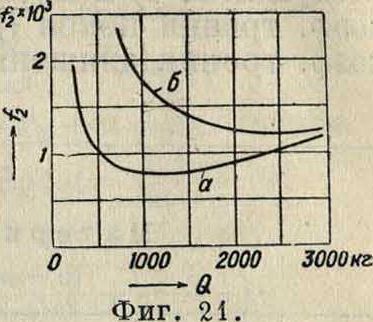
шипа при смазке минеральным маслом. Для практического использования гидродинамической теории смазки в том виде, как она развита проф. Н.И. Мерцаловым, необходимо для определенности расчета подшипника знать хотя бы приближенное очертание этой траектории. За _рт_ таковую наиболее удобно ^μ принять полуокружность

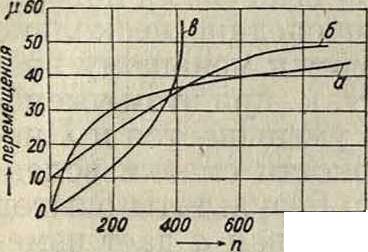
т тооб/н.

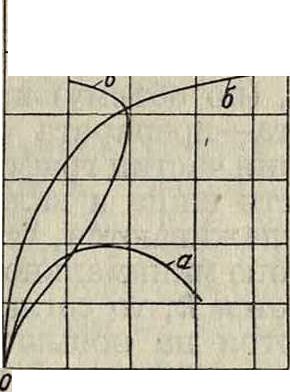
Фигура 22.

zoo 400 eoo 8оооб/и.

Фигура 23.

с диаметром r_x —r₀= toy, соединяющим центры шипа О и подшипника 0_Х при крайнем нижнем положении шипа. Тогда при любом положении (фигура 24) эксцентриситет е₀ и угол θ_χ будут связаны зависимостью е₀=(г_х — г о) cos 0_Х=г{к, cos 0_Х. Пренебрегая за малостью к величиной 2к, сравнительно с единицей, имеем (смотрите ст. 829)

^е0

Χι (1 + 2й) — х_х

вследствие чего

17 =

Ро=:

-=0,658-

16/3ftS(5C*-i) ’ β№(χ -1)

Путем тех же упрощений и преобразований выражение коэф. трения обращается в

А=0,658 ---^μηΧι

PPoh-V х - и далее, как выведено на ст. 848, Я=7с Ух — 1.

Приравнивая правые части (10) и (11), приходим к ур-ию

- 0,658^-ж_х-1=0,

к-рое определяет х_г: ·__

®ι=0,329 + /( 0,329 ^-_fe)² +Т

Коэф. х_х можно выразить также через наименьшую толщину зазора (смазочной пленки) h, то есть

fcr_x

ж,=-г¹ =

Ьгх

_8ΐηβι-)/ι-(^)·-%2.

Выражение давления, перпендикулярного линии центров, преобразуется тогда в

Р _ 8πμϋΧι

^{1 _} ’

При переводе Р_х кг/м, представляющего собой нагрузку на 1 ж длины подшипника, в удельные давления на 1 м² проекции поверхности шипа получаем

Pi=2r„p,

где Р—ординаты давления, распределенного равномерно в средней части подшипника. Т. к. по направлению к концам подшипника давления падают до нуля, то в дальнейшем необходимо ввести поправочный коэф. β:

ν=ν«β,

где ро—среднее давление, равномерно распределенное по всей длине подшипника, с которым обычно приходится иметь дело в технич.^ расчетах. Проверка теории на основании имеющихся опытов позволяет принять этот коэф. равным

Р I + 4 d

β⁼ ϊ ’

где I—длина, a d—диам. шипа.

Выражая далее окружную скорость шипа через число оборотов, то есть

2 пг₀п ‘ 60 ’

получим

π^μηχχ _пого 1™^χι

(9)

(10)

(И)

(₀ Ητχ-h

Очевидно, что, чем меньше h, тем ближе ж_х к единице и тем меньше на основании (11) коэф. трения Я, приближающийся к нулю. Практически однако Я не достигает нуля, т. к. с приближением поверхности шипа к поверхности вкладыша наступают явления, не учтенные теорией,— вихревые движения в смазоч

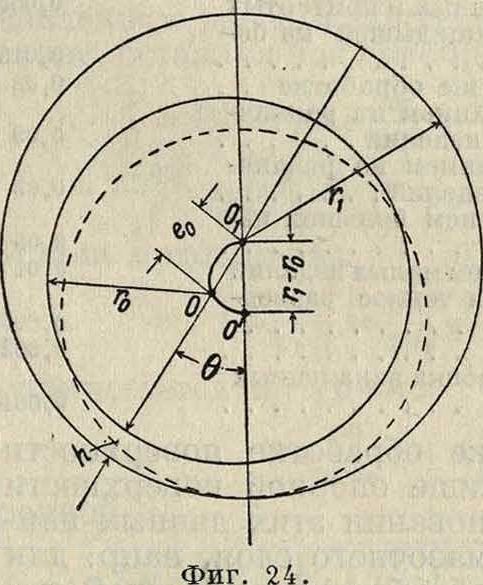
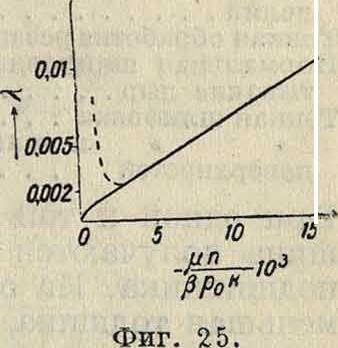
ном слое, трение пограничных слоев, к-рое имел еще в виду Петров, и наконец полужидкостное· трение, переходящее в сухое. На фигуре 25 показан: ход изменения коэф. Я при к= ^ и различных. причем пунктирная кривая значениях

μη

βΡο*· ’

намечает возрастание Я при переходе предельного значения. Итак, для минимума Я необходимо иметь в самом узком месте зазора наименьший смазочный слой. Величина последнего зависит от обработки шипа и вкладыша. Как бы тщательно ни велась обработка, на их поверхностях всегда останутся мельчайшие выступы и впадины. При продолжительной приработке-шип снашивается на среднюю толщину выступов его <5₀ до диаметра 2г₀ (фигура 26), а у подшипника

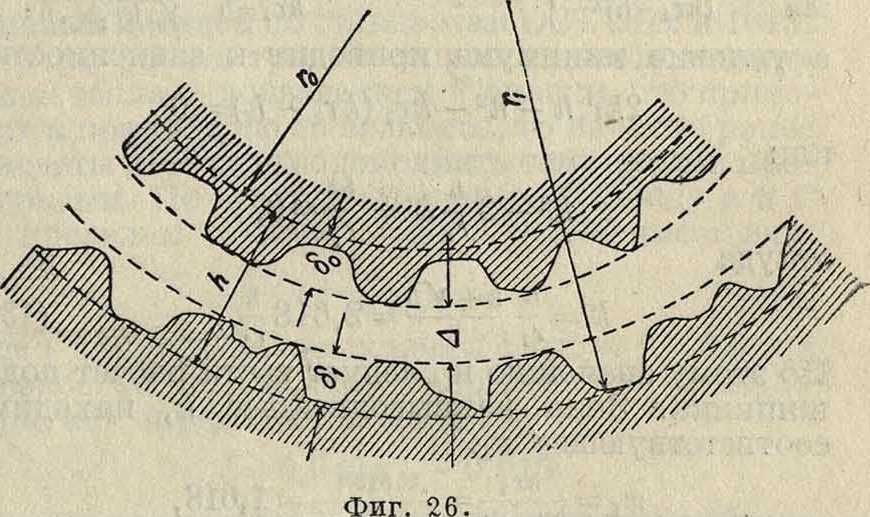
снашиваются выступы б_х и диам. его обращается в 2г₀. Таким образом минимальная толщина смазочного слоя, необходимая, чтобы соответствующие выступы при сохранении смазки между ними не задевали друг друга, равна 7г=<5_х -f б₀. Таблица 5 характеризует толщину выступов (по наблюдениям проф. Брандта) для обработанных, поверхностей изделий из мартеновской стали.

Обточенная 0,03—0,04

» и шлифован, полуличной пилой о,02—о,03

» » » ЛИЧНОЙ » 0,01—0,02

Чистообточенная и шлифованная наждачным полотном № 1 .. 0,008—0,007

Чистообточенная и шлифованная наждачным кругом.. 0,001—0,005

Обработанная чистовым резцом и шлифованная наждачным полотном № 00 Гили закаленная и шлифованная). 0,003—0,001

Плоская поверхность, чисто пришабренная по чугунной плите.. 0,001—0,003

Плоская поверхность, закаленная и весьма чисто притертая по чугунной плите. ок. 0,0001 Для опорной поверхности чугунных подшипников, обработанных разверткой. 0,005

Для бронзовых вкладышей, пришабренных по калибру, с диам, соответствующим диам. подшипника, а также выглаженных, уплотненных и прите ртых 0,005

Для чисто сверленых вкладышей из белого металла.. о, 015

Для бронзовых при той же обработке. 0,02

Обычная обработка резанием на различных станках больших изделий. 0,09

Обычная обработка резанием на различных станках малых изделий. 0,03

Тонкая обработка резанием больших изделий 0,05

Тонкая обработка резанием малых изделий о, οι

Нормальная шлифовка и тонкое развертывание дыр.. 0,005

Тонкая шлифовка.. 0,002

» » и полировка закаленных поверхностей.. ο,οοί

При одной и той же обработке поверхности шипа получаются чище опорной поверхности подшипника. На основании этих данных наименьшая толщина смазочного слоя, например для поверхности шипа, обработанного личной пилой, и чисто сверленых бронзовых вкладышей, равна при нек-ром запасе А=0,005 миллиметров

h - δ₀ + <5_Х + Δ=0,015 + 0,02 + 0,005=0,04 миллиметров.

Считая в дальнейшем h величиной постоянной, найдем необходимый относительный зазор к, исходя из минимального значения коэф-та трения. Ф-ла (11) на основании (12) преобразовывается в __

*=*

Согласно этой зависимости на фигуре 27 представлен ход измщшния Я в зависимости от величины к при /i=0,04 миллиметров и г_х — 50 миллиметров. Производная Я по к дает

dx _ [kr-h)~r₁k γο^τψ-τϊ i ^k__^ГЛ,

а условие минимума приводит к зависимости 2кг Ji — h² — lcr₁ (lcr_L — К)=0

или

“,._зА* ₊ £=_0>

откуда

^7c=£^3J^=²>⁶¹⁸£· (13)

По этому значению и следует вести расчет подшипника. Зная наивыгоднейшее /с, находим соответствующее х±

г — ^kVl — ²’⁶¹·⁸^ ₌ 1 C1Q

¹ kr_x-h 2,618/1-1 ’ ’

а по нему наименьшее значение коэф. трейия, к-рое можно назвать конструктивным минимумом трения,

Я=к Ух² - 1=к У1,618² - 1=1,2727с. (14)

Т. о. конструктивный минимум Я зависит исключительно от геометрических размеров: диаметра

шипа и подшипника, то есть от их относительного зазора, причем последний зависит от выбранной наименьшей толщины смазочного слоя. Хотя эти выводы и являются следствием нек-рых приближений, внесенных в строгую теорию трения смазочного слоя, но они хорошо подтверждаются опытами Е. Шнейдера, к-рый определял коэф. трения при смазке, содержащей 2% (по объёму) примеси коллоидального графита—препарата «Коллаг». Вследствие осаждения частиц графита между выступами поверхности шипа и вкладыша последние несколько заглаживаются, что приводит к меньшему значению минимального h. Ат. к. при этом уменьшается к, то согласно (14) уменьшается и Я несмотря на повышение вязкости смазки вследствие графитовой добавки. Результаты опытов представлены на фигуре 28. Кривая а дает изменение Я при расходе смазки 200 см³/час, кривая

4г

0,01

·<.

1 от о,т·

о10 50 юо

— Н.Ю“

Фигура 27.

	б			аГ
		/ν	а
вл			Т

—/? Фигура 28.

гоооб/и. б—при расходе, в 20 раз меньшем,—ему и соответствуют большие значения Я. Прибавка графита дает соответственно кривые виг, лежащие ниже кривых а и б. Как видно из фигура 28, прибавка графита является особенно полезной при малых числах оборотов и плохой смазке, когда выступают явления полужидкостного трения. Последние всегда наблюдаются в период разгона машин и при трогании с места подвижного состава. Присадка графита является т. о. средством к уменьшению большого начального сопротивления движению, что должно иметь особое значение в железнодорожном деле. Отметим попутно, что общепринятая в Германии гидродинамич. теория трения проф. Гюмбеля находится в полном противоречии с только что рассмотренными опытами. По Гюмбелю коэф. трения равен

Я=3

8l/l“

’ У Ро

Следовательно повышению вязкости смазки от прибавки графита должно соответствовать возрастание Я, а изменение коэф. трения должно происходить по закону параболы. Но ни то ни другое кривые фигура 28 не обнаруживают. При найденных значениях х_х и к зависимость (9) обращается в

Ро=0,658-^^=0,658 ^

(15)

Минимум коэф. трения отчетливо получился в опытах Штрибека, где он оставался постоянным и независимым от числа оборотов и давления (фигура 14). Штрибек не приводит ни относительного зазора в своем испытуемом подшипнике Селлерса с диам. d=70 миллиметров и рабочей длиной 1=230 миллиметров ни вязкости смазки. Однако и то и другое легко вычисляются по ф-лам (14) и (15). В этих опытах минимум трения установился равным Я=0,0035, следовательно относительный зазор подшипника к-·

°,°°35 ₌ 0,00275=·^

1,272 1,272

Ряд кривых дает этот минимум при среднем отношении числа оборотов к давлению —=8, где р₀ взято в килограммах/см². Следовательно вязкость смазки при постоянной ί° опыта 25° и поправочном коэф-те

_п 230 +4-70 о о о р=- Ш~=^г>^гг

равна μ =

βρο№ _ 2,22-10 000

= 0,0288 килограмм ек/м².

0,358 η 0,658 · 8 · 334²

Однако совершенно недопустимое устройство смазочных канавок на опорной поверхности вкладыша подрывает ценность опытного материала Штрибека и не позволяет на его коэф. трения проверить ф-лы теории. Более совершенные опыты Лаше с подшипниками d=200 миллиметров,

I=400 миллиметров, ,1с -

17

при U=30 м/ск (что соот ветствует п=2 860 об/мин.), коэф. вязкости μ== 0,001кг ск/jti², р₀=6,5 килограмм/см² дали коэф. трения λ=0,006. Поправочный коэф. при этом равен β=-=3. Значение х_г:

4υ

0,359 - 0,001 - 2 860

^Ж1 3- 3,5 - 104-172.10-8 ¹

+ Vl,69*+ 1=1,69 + 1,96=3,65, чему соответствует коэф. трения л=к У^1=ж, № =

17

10 000

3,51=0,00597.

Совпадение вычисленного коэф. с опытным прекрасное. Применим найденные ф-лы к расчету подшипника при d=2гу=100 миллиметров с наименьшей толщиною смазочного слоя, взятой в качестве примерной выше:

h + <5₀ + <?! + Δ=0,015 + 0,02 + 0,005=0,04 миллиметров.

Исходя из условия конструктивного минимума трения, найдем необходимый относительный зазор к=2,618 £=2,618=0,0021=·

Т. к. наибольший эксцентриситет при этом с =г₁ — г₀=кг у=2,618 h=2,618-0,04=0,105 миллиметров, то диаметр шипа

d₀=dy — Ze— 100 - 0,21=99,79 миллиметров.

На поверхности шипа и подшипника с размерами d₀ и dy нужно смотреть, как на идеально гладкие. Действительные размеры диаметра шипа d₀и подшипника d’y, получаемые при измерении с учетом выступов, равны:

<=2г₀ + 2<5₀=99,79 + 2 · 0,015=99,82 миллиметров, d[=2r_t —=100 — 0,04=99,96 миллиметров.

Расчет несколько меняется, если приходится исходить из действительного размера диаметра шипа. Пусть do=100 миллиметров. Т. к. г₀=г’₀ — <5₀ и то теоретический относительный

¹---Г-

зазор к=2,618 уг—

’ Г — On

или к

2,618/1

о)+2,618/1

Числовой подсчет дает

2,618 -0,01

г=0,00206=-

‘50-0,015+2,618-0,01 485

Действительный радиус подшипника при этом

Г, =

^ι-*ι-

_ 49,985j_185 484

0,02 =

1-/1

= 50,09 — 0,02=50,07 миллиметров,

а действительный относительный зазор

Ί»^г __ ^Г~^Го__ М? ₌ 1

г[ 50,07 715

Связь между идеальным и действительным относительным зазором устанавливается равенством

_{k=r +} So + di

^Г1

Пусть далее даны нагрузка на подшипник Q== 2 000 килограмм и число оборотов вала п=400 об/мин. Имея в виду в качестве смазки масло «машинное 2» (ОСТ 274), зададимся абсолютной вязкостью μ — 0,003 килограмма ск/м², что несколько ниже вязкости этого масла при ί°=50°. Т. к. расчет ведется при условии конструктивного минимума трения, то, пользуясь ф-лой (7), находим при найденном ранее к допускаемое удельное давление, оставляя пока неопределенной поправку

β

177 000 β

= Р„=0,658

μη 0,003-400- 476^г

7гг/ж² или Vo=~j =

Р 17,7

Длина подшипника г =

Q

Ро^о ’

01. Pd₀ "

Q(l + pd₀l

кг/см².

определяется из ур-ия I²

равной г

-5-1- 4-=0

Pd о Р

⁼ Sr_o ⁺ ViSio) +⁴|-⁵>65 + + У31,92 + 226,0=21,65=22 см,

Т. Э. т. XXIV.

причем среднее удельное давление

ρο=|-_ί=ι^=⁹-^{1 килограмм}^·

Для уменьшения длины подшипника выгодно иметь большее р₀, что можно достичь, выбирая смазку повышенной вязкости и уменьшая относительный зазор к, что к тому же дает и меньшие значения конструктивного минимума коэф. трения. Но уменьшение к возможно лишь с повышением качества обработки смазываемых поверхностей. Этот вопрос решается в области технологии, практика которой устанавливает зазоры в подшипниках путем нормализации допусков и посадок при различных классах точности. Ниже приводится табл. 6 зазоров различных посадок по стандартам ОСТ 1012 и 1013.

Т. к. работа трения сопровождается выделением тепла и повышением t° смазки, что приводит к понижению ее вязкости, то начатые ранее расчеты необходимодополнить темп-рными проверками. По Фальцу зависимость между μ и Г в пределах от Г=25° до ί°=100° имеет вид:

^μ ~

где г для минеральных масел суд.в. у=0,9 и с вязкостью по Энглеру в пределах от 2 до 24 при 50° определяется из ф-лы:

i=0,045£7₅₀ — 0,015.

Максимальная Г t_max, допускаемая при выбранной смазке и всех прочих расчетных условиях, определяющих конструктивный минимум коэф. трения, определится тогда из ур-ий (7) и (8):

tmax — 10 ~у/~ 0,658 -ρρ^ϊ ·

Т. к. для масла «машинное 2» E_i0=5,5-6,2,

28

Класс точности	Посадка	• Применение	Диаметры отверстий в миллиметров	Зазор в μ
II	Ходовая	Переборы и основные подшипники в токарных,	30— 50	35- 50
	X	фрезерных и сверлильных станках. Коренные	50— 80	30— 60
		подшипники коленчатых валов, а также верх-	80—120	40— 75
		ние и нижние подшипники шатунов автимо-	120—180	50— 9)
		Сильных моторов. Подшипники шестереночных	180—260	60—105
		редукторов и червячных передач
	Легкоходовая	Подшипники ходовых винтов супортов, а так-	30— 50	50— 85
	Л	же валов на нескольких ( > 2) подшипниках	50— 80	65—105
		у станков	80—120	80—125
			120—180	100—155
			180—260	120—180
	Широкоходовая	В точных трансмиссиях и контрприводах. В	30— 50	75—115
	Ш	валах турбогенераторов и других быстро вра-	50— 80	95—145
		щающихся машин	80—120	120—175
			120—18.)	150—210
			180—260	180—250
III	Ходовая	Коренные подшипники коленчатых валов, а	30— 50	32—100
	Хз	также подшипники шатунов и валов паровых	50— 80	40—120
		машин и двигателей внутреннего сгорания.	80—120	50—140
		Эксцентриковые хомуты. Подшипники динамо-	120—180	60—165
		машин, центробежных насосов, вентиляторов	180—230	75—195
	Широкоходовая	Осевые буксы повозок, подшипники сел.-хоз.	30— 50	75—160
	Ш з	машин, подшипники трансмиссий, холостые	50— 80	95 -195
		шкивы	80—120	120—235
			120—180	150—275
			180—230	180—330

находим, приняв Е - 0,015=0,255. При Г‘2,6

t max ⁼ Ю

α= 6> ЭТОМ

что i=0,045 · 6 —

0,658

0,255 · 400

17,7 ·10*

= 10 101,5=57°.

Для нахождения действительной t° подшипника воспользуемся ф-лой теплоты лучеиспускания, предложенной Фальцем:

Qo=nA(t_c — i_fi)M Cal/ч ж², (9)

где t₀—темп-pa смазки, t_b—темп-pa воздуха, А— коэф., зависящий от состояния внешней среды и конструкции подшипника, Q_a — количество тепла, излученного с 1 ж² боковой поверхности шипа в час. Т. к. полное количество тепла, развиваемого работой трения, равно

q=_ з _{600 =} · 3 600 =

= 2лг₀1 · 0,S51P_olir_on,

то на 1 ж² боковой поверхности шипа приходится тепла

βι=ί^ϊ=·.Μ67Ρ^₀«. (Ю)

Сопоставляя (9) и (10), находим

i С³ 0,357P₀Jtr₀n С - У -17 - А

к

(Н)

Значения коэф.Д по Фальцу приведены в таблице 7. Для пальца кривошипа в зависимости от скорости V значения А можно принять,как указано ниже:

V, М/СК ДО 1123 t 5 6 7 89 Ю 12 А. 2,3 3 4 4,8 5,5 6,1 6,6 7,1 7,6 8 8,4 9,2

Принимая для начатого выше примера А=1, находим при t_c=20° рабочую f смазки по формуле (11)

х.о

*«=у

0,37	5 -91 000-0,05 · 400
84,4	17 · 476 = 30,3° + 20°

+ 20° =

Таблица 7. — Значение к о э ф и ц и е н т я А по <1> а л ь н у.

	Состояние среды
Тип подшипника	В спокойном воздухе	Вентиляция шкивом или маховиком с одной стороны	Вентиляция с обеих стором
Подшипники малых размеров несложной конструкции; смазка капельной масленкой.	0,7	1,5	2
Подшипники средних и крупных размеров —трансмиссионные, кривошипные; кольцевая смазка.	1	2,5	3

Т. о. вязкость масла «машинное 2» вполне удовлетворяет давлению, скорости вращения вала иконструкции подшипника, т. к. i_c<i_OTra.

Для равномерного распространения и притока смазки к опорному вкладышу, то есть для поддержки постоянства смазочного слоя, на внутренней поверхности вкладышей обычно устраиваются различного рода смазочные канавки. Наличие последних однако часто противоречит основам гидродинамич. теории трения и приводит к результатам, прямо противоположным назначению этих канавок. Для вращающегося шипа канавки на опорном вкладыше одинаково вредны, идут ли они продольно, диагонально или имеют кольцевое очертание. Т. к. они сообщают область повышенного давления с низким давлением, то они всегда способствуют понижению давления той части смазочного слоя, которая находится перед наиболее узким местом зазора, которая собственно и поддерживает шип на масляной подушке внутри подшипника. Понижение давления может привести к разрыву смазочного слоя, то есть кполу-жидкостному трению, к-рое не м. б. устранено большим расходом смазочного масла. С этой стороны особенно вредной является осевая канавка на опорном вкладыше с отверстием посредине для спуска смазки. Примером такого неправильного устройства опорного вкладыша является представленный на фигуре 29 подшипник, с которым производил свои опыты Штрибек.

Смазка при вращающемся шипе должна подводиться или сверху со стороны ненагруженно-го вкладыша и оттуда уже увлекаться благодаря своему свойству «липкости» самим шипом в направлении его вращения или подводиться сбоку в боковые канавки. Последнее устройство применяется в турбинных подшипниках AEG (Берлин) (фигура 30). Здесь смазка подводится под давлением с обеих сторон шипа, у о заполняет глубокие продольные канавки и радиальный зазор между шипом и подшипником, а выход ищет себе на ненагруженной стороне вкладыша в осевом направлении к обоим концам подшипника. Смазочные канавки на опорной поверхности вкладыша допустимы лишь при малых скоростях вращения, где все равно нельзя ожидать жидкостного трения.

Фигура зо.

В таком случае они должны сходиться под углом по направлению вращения шнпа и не доходить до концов вкладыша, где давление в смазочном слое падает (фигура 31). Такого же. рода канавки допустимы при возвратновращательном движении шипа и на опорных направляющих и при возвратно-поступательном движении.

Чтобы канавки не соскребали смазки, они должны иметь плавно округленное очертание. Во вкладышах, где возвратно-поступательное

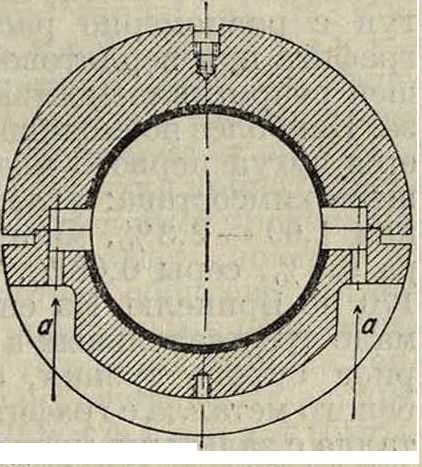
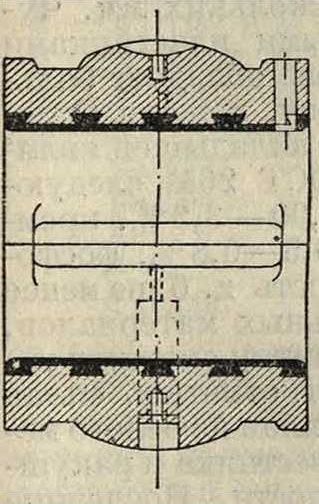
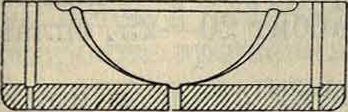
Фигура 29.

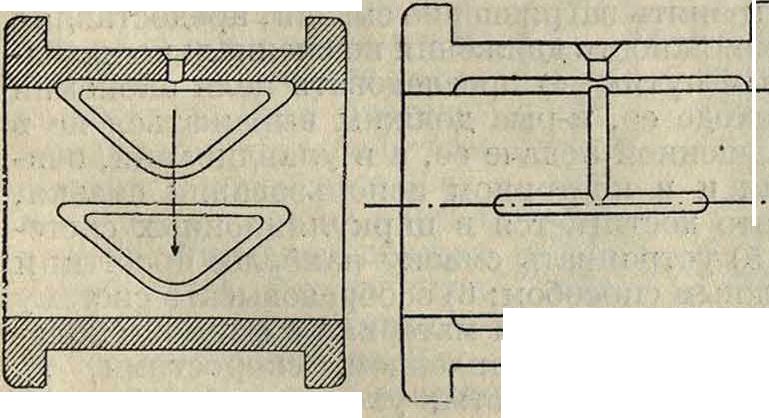
Фигура 31.

-i

Фигура 32.

движение шипа сопровождается переменой направления давления, например в подшипнике крейцкопфного болта, смазочный слой является буфером, смягчающим удары в мертвых положениях. Здесь смазка должна подводиться в короткие продольные канавки, расположенные на тех сторонах подшипника, где перемена давления вызывает наибольшее всасывание ее (фигура 32). Продольные канавки соеди

п	1
Ж
U tJ

Фигура зз. няются полукружной средней канавкой. В качающихся подшипниках без перемены давления полное жидкостное трение невозможно, и чтобы обеспечить смазывание скользящих поверхностей, здесь необходимо на нагруженной стороне вкладыша иметь несколько продольных канавок, соединенных средней кольцевой (фигура 33). Радиальный зазор может быть доведен до нуля. Для того чтобы радиальный зазор при вращающихся шипах оставался по всей длине подшипника достоянным, необходимо, чтобы вкладыши последнего самоустанавливались. При больших нагрузках во избежание значительных деформаций шипа, для устранения переко- =·--¹-~·

сов, которые могут привести к сухому трению, и вообще для более равномерного распределения давления вдоль него шип должен быть коротким. Приведенный выше на фигуре 30 новейший подшипник для турбины AEG удовлетворяет всем этим условиям. Вследствие деформаций вала и самого шипа он устанавливается в подшипнике так, как это преувеличенно представлено на фигуре 34. Во избежание сухого трения необходимо, чтобы

D>d COS a + f COS a + l tg a, где a—угол наклона, составленный касательной к концу оси вала с горизонталью, f—стрела прогиба шипа внутри подшипника. Это условие приводит к неравенству D-d ^ !, i ₊„

D ^> D D “ ·

При длине вала L и сосредоточенной нагрузке Р посредине его

. PL²

tg “=йГрТ

lb ill нала что через удельное давление на двух подшипниках выражается как

tg α= ·

®^л-‘вала

Прогиб шипа внутри подшипника равен f _ Jl Ρο^ι1ί

8 EI_шииа следовательно написанное выше неравенство

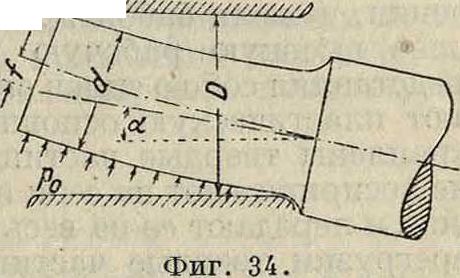
переходит при Ό=d + к в неравенство:

и может служить к проверке выбранного относительного зазора к. При самоустанавливаю-щихся подшипниках второй член суммы, стоящий в скобках, отпадает. В те моменты работы шипа, когда смазка вытесняется под большим удельным давлением, выступает роль материала вкладышей подшипника. Последние должны изготовляться из специальных антифрикционных сплавов, обладающих следующими свойствами: 1) малым коэфициентом сухого трения, 2) высокой теплопроводностью, 3)"сопротивляе-мостью разъеданию и ржавлению, 4) проч-

ностью, чтобы не сминаться и не разрушаться под давлением шипа, и 5) твердостью, чтобы сопротивляться износу. Твердость материала вкладыша должен быть однако менее твердости самого шипа, чтобы избежать износа последнего. Наиболее распространенными сплавами для вкладышей являются бронзы и баббиты. Состав оловянных бронз примерно следующий (в %):

Медь. .. 85 82 82

Олово.. 13 15 10

Цинк.. 2 3 8

Более дешевыми являются бронзы свинцовые, к которым добавляется один процент никеля в целях равномерного распределения свинца в сплаве. Состав их следующий (в %):

Медь. 69 63 60 Олово. 8 9 5

Свиыец. 22 25 ВО Никель. 1 1 1

В фосфористых антифрикционных бронзах вместо никеля вводится от 0,1 до 0,3% фосфора. Антифрикционная бронза имеет предел упругости около 1 000 килограмм /см². Твердость по Брине-лю 60—80. Она труднее прирабатывается к шипу, развивая при этом более высокий коэф. трения, нежели баббиты, и следовательно дает более высокую рабочую 4°. Баббиты (смотрите), представляя собою сплав олова, меди и сурьмы, дают пластическую основную массу, в к-рую вкраплены твердые частицы сурьмы. Последние воспринимают на себя нагрузку со стороны шипа и передают ее на весь вкладыш. В случае перегрузки твердые частицы вдавливаются в основную массу и тем выравнивают распреде

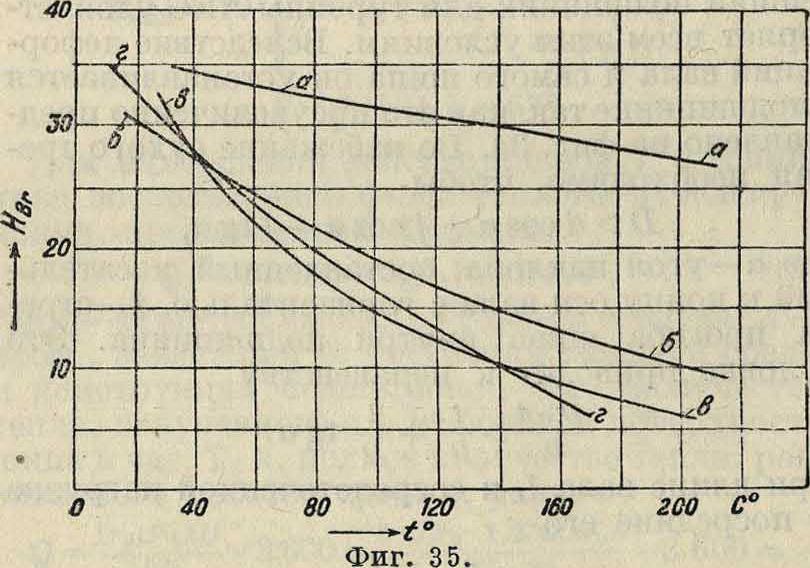
ление давления. В условиях полужидкостного трения основная масса изнашивается быстрее твердых частиц, и шип оказывается поддерживаемым выступающими твердыми вкраплениями, между которыми может циркулировать смазка, вынося частицы износа и охлаждая поверхности скольжения. Помимо баббитов с оловянной основой последнее время находят большое применение сплавы с цинковой основой. Для образования твердых частиц вместо сурьмы здесь употребляются барий, кальций, натрий, калий, литий, магний, дающие в химич. соединении со свинцом и медью твердые структурные вкрапления. К таким сплавам относятся сплав Лурги, введенный в Германии во время войны (состав его: свинца 96,5%, бария 2,8%, кальция 0,4%, натрия 0,3%) и сплав Canmetall с составом: свинца 94,9%, кальция 1,75%, стронция 1,0%, бария 1,0%, меди 1,35%. В америк. пром-сти для подшипников употребляется сплав,содержащий ртуть; (состав его: свинца 96,75%,кальция 1,0%,ртути 0,25%). Пределы упругости при сжатии белых антифрикционных металлов таковы: оловянный баббит 200 к г/см², свинцовый баббит 200 килограмм 1см², сплав Лурги 330 килограмм/см². Твердость по Бри-нелю при комнатной температуре: оловянный баббит 30—34, свинцовый баббит 20—25, сплав Лурги 28—36.

При Г в 100° твердость этих сплавов понижается на 30—50%. Зависимость твердости по Бринелю (Н_Вг) для различных сплавов от t° представлена на фигуре 35 (а—бронза, б—сплав Лурги, 6 — оловянный баббит, 8—свинцовый баббит). Из других свойств антифрикционных металлов отметим нижеследующие: металлы, богатые оловом, обладают более высокой теплопроводностью, нежели содержащие в основе свинец. Бронза и сплавы, содержащие цинк, изнашиваются сильнее сплавов, богатых свинцом, но последние имеют более высокий коэф. трения. Стойкостью против разъедания маслами обладают сплавы, содержащие олово и сурьму. Меньшей стойкостью обладают железо и медь, а в особенности свинец и цинк. Вполне пригодным материалом для вкладышей является чугун. После обработки он дает твердую гладкую поверхность, в отношении которой масло проявляет хорошую прилипаемость. Вследствие пористого строения чугуна смазка пропитывает поверхность его на глубину нескольких миллиметров. Чугун с равномерно рассеянными пластинками графита при перлитовой основе обладает большей сопротивляемостью износу, нежели бронза. Наиболее подходящим для вкладышей является чугун первого класса (ОСТ 265) следующего химсостава: углерода 3,00—3,3%, кремния 1,09 — 2,3%, марганца 0,5—0,8%, фосфора 0,8%, серы 0,08%. Твердость должен быть не менее 170 по Бринелю. Из специальных материалов, мало чувствительных к недостатку смазки в период сухого трения, следует отметить сплав белого металла с графитом и сплав из белого металла с залитыми кусками известняка и ракушника соответствующей твердости. Последние вкладыши, тщательно проточенные, хорошо полируют цапфу, впитывают в себя смазку, вследствие чего еще долгое время могут работать без значительного нагрева при прекратившемся притоке ее.

Системы смазни. При выборе системы смазки следует руководствоваться следующими общими требованиями: 1) смазка должен быть наиболее совершенной, то есть жидкостной; 2) нужно стремиться к автоматичности подачи смазки и независимости от обслуживающего персонала; 3) устранять загрязнение смазки, предоставляя ей Возможность движения по специально назначенным путям; 4) преследовать цели экономии в расходе ее, которые должны выражаться не в уменьшенной подаче ее, а в улавливании, очищении и в повторном использовании смазки, как это достигается в циркуляционных системах; 5) устраивать смазку наиболее простым и надежным способом; 6) сообразовывать систему смазки и смазочный материал с формой скользящих деталей, давлением, скоростями, t°, длительностью работы, уходом, окружающей средой и с особенностями того материала, для которого назначена машина или станок, наир, ткань в ткацких станках. Наиболее распространенным смазочным материалом является минеральное масло, которое употребляется в следующих системах смазки.

Смазка при помощи ручной масленки. При этом способе, как и при других ниже рассматриваемых способах подачи” смазки без давления, смазка попадает к

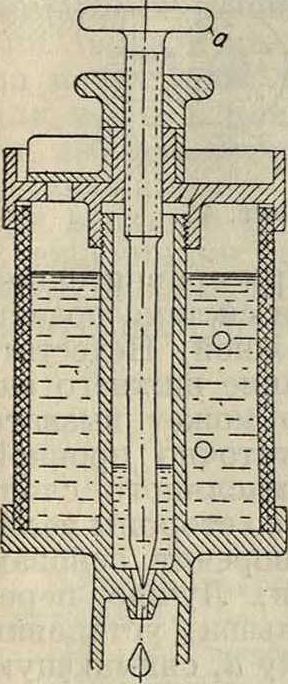
Фигура 36.

месту потребления самотеком под действием силы тяжести и благодаря прилипанию ее к скользящим поверхностям. Ручная смазка применяется в подшипниках тех машин, где малые скорости вращения и нагрузки или движение совершаются периодически с возвращением в состояние покоя, то есть где жидкостное трение вообще невозможно. Этот род смазки применяется также при открытых скользящих поверхностях, легко доступных для ухода, или там, где машина находится под непрерывным наблюдением, например в станках по металлу.

Капельная смазка применяется там, где ручная смазка является неудовлетворительной или неудобной по условиям обслуживания. Преимущество капельных масленок: они дают равномерное питание и допускают некоторую регулировку в подаче смазки. Недостатком их являются зависимость числа капель от t° и уровня масла в масленке и необходимость неподвижной вертикальной установки их. По своему действию капельные масленки разделяются на несколько типов: а) В капельной масленке с отверстием (фигура 36) количество капель в единицу времени регулируется винтом а путем открытия конич. отверстия. Постоянный уровень масла здесь поддерживается по принципу сообщающихся сосудов, находящихся под различным внешним давлением. Для исправности работы этой масленки смазка должен быть тщательно очищена от всяких механич. примесей, б) Штифтовая (бутылочная) масленка (фигура 37) состоит из стеклянной опрокинутой масленки а, во внутреннем канале которой находится штифт б, опирающийся непосредственно на вал. Вибрация и толчки со стороны вала передаются игле, которая приходит в движение, способствуя стеканию масла по зазору в канале. Регулировка достигается подбором штифта большего или меньшего диаметра, что является способом довольно несовершенным. Достоинство этой масленки—ее автоматичность (она работает лишь при вращении вала) и полная защита масла от засорения, в) Фитильная маслен-к а (фигура 38) подает масло каплями на вал благодаря капиллярным свойствам фитиля. В качестве последнего применяется чистая J| шерсть. Фитиль не должен иметь узлов. Регулировка ^//////Δ подачи масла в этой масленке весьма ограничена. К достоинствам ее надо отнести способность фильтровать масло и возможность установки на подвижных машинных деталях, г) Клапанные масленки доставляют масло в нужные моменты периодически при помощи толкателя, связанного с подвижной деталью; толкатель, действуя на клапан, выполняемый в форме шарика, открывает отверстие в масленке, создавая автоматически выход смазке. На фигуре 39 клапанная масленка применена к смазке дыропробивного пуансона. Тот же принцип м. б.

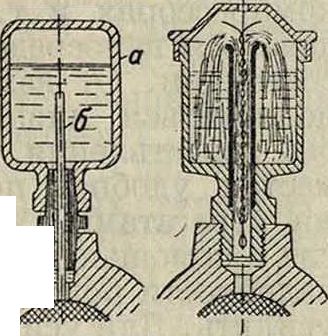
Фигура 37. Фигура 38. -

применен к смазке крейцкопфного подшипника (фигура 40). Здесь наклонная плоскость а, присоединенная к ползуну, открывает шаровой клапан б, снимает масло с шарика и позволяет ему стекать к месту подачи смазки. При передаче смазки рт неподвижных масленок к вращаю

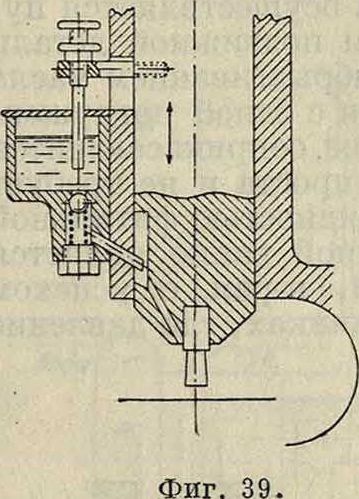
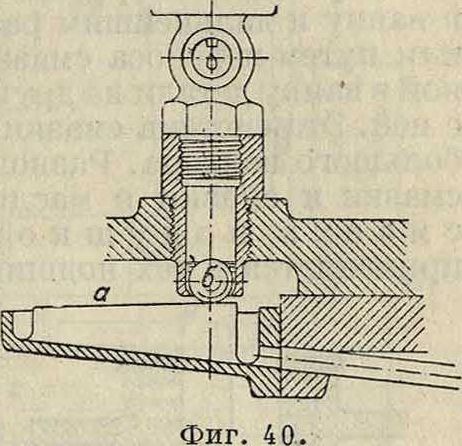
щимся или качающимся деталям пользуются раздвижными трубками и коленчатыми трубками с полым шарниром, проводящим масло. Для смазки пальца кривошипа или шеек коленчатых валов целесообразно используется

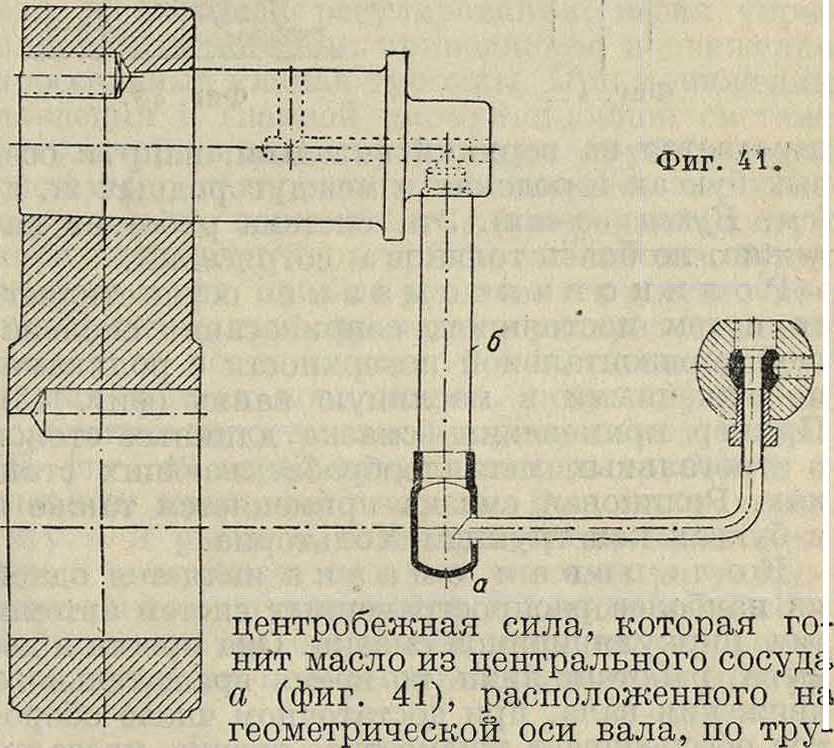
бке б в канал пальца кривошипа, или применяют для коленчатых валов (смотрите) кольцевой жолоб, концентричный с осью коренной шейки коленчатого вала.

Центробежная смазка как самостоятельная система применяется в вертикальных валах при значительном числе оборотов (фигура 42). Эта система относится к простейшим циркуляционным системам смазки.

Винтовая смазка использует восходящее движение смазки по винтовой канавке на валу при вращении последнего (фигура 43). Эта система используется в вертикальных валах, где осевая нагрузка преобладает над радиальной, т. к. при больших боковых удельных давлениях винтовая канавка препятствует образованию устойчивого смазочного слоя.

Смазка гребнем применяется для смазки направляющих в вертикальных поршневых машинах, в лесопильных рамах и тому подобное. Смазочный гребень а (фигура 44), привернутый на конце возвратно движущейся детали б, погружается при каждом ходе в масленку в и смазывает поверхности скольжения. Избыток смазки стекает в ту же масленку вниз.

Смазка в масляной ванне применяется для компактных механизмов, расположенных в коробках или кожухах, непроницаемых для масла. Таковыми являются кривошипные механизмы маломощных моторов, зубчатые редукторы, червячные передачи, подпятники вертикальных валов, веретена прядильных машин ит. п. Смазка осуществляется путем периодич. погружения подвижной детали в ванну и дальнейшим разбрызгиванием масла или путем переноса смазки с одной погруженной в ванну детали на другие, соприкасающиеся с ней. Эта система смазки проста и не требует большого надзора. Разновидностью фитильной смазки и смазки в масляной ванне является смазка подушкой, которая с успехом применяется в тех подшипниках, где давление

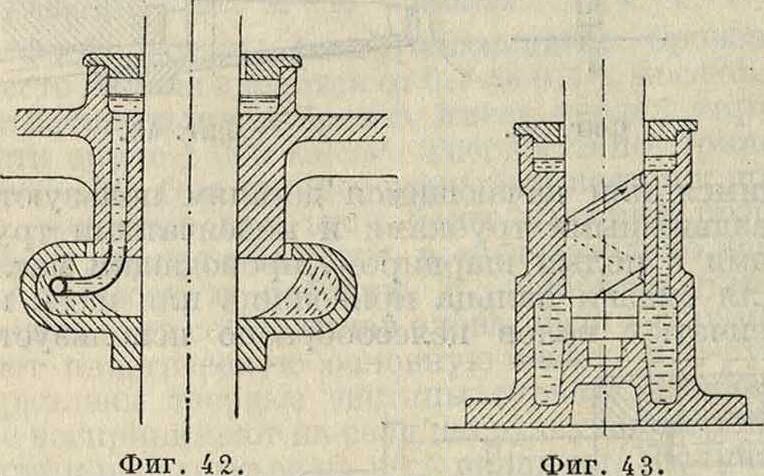
передается на верхний вкладыш, напримерв осевых буксах городских и междугородных ж. д. (смотрите Букса осевая). Эта система работает надежно, не боясь толчков и сотрясений.

Роликовая смазка осуществляется путем постоянного соприкасания скользящей горизонтальной поверхности с роликами, погруженными в масляную ванну (фигура 45). Пример применения—смазка длинных столов в строгальных металлообрабатывающих станках. Роликовая смазка применяется также и в буксах конструкции Хольторна.

Кольцевая смазка является одной из наиболее распространенных систем автома-тич. циркуляционной смазки. Она проста и дешева, работает лишь во время вращательного движения вала, при достаточном числе оборотов обеспечивает жидкостное трение, предъявляет небольшие требования к уходу и поэтому может быть применена для тех подшипников (смотрите), которые мало доступны по своему расположению, например под потолком, в подвалах. Т. к. масло находится в избытке в масляной ванне, защищенной от засорения, то отпадает необходимость в очистке масла в течение длительного промежутка времени. В системе смазки со свободным кольцом последнее прорезает верхний подшипник, висит свободно на валу, погружаясь своей нижней частью в масляную ванну. Подача смазки зависит от сечения кольца, его размеров, числа оборотов вала, вязкости масла и липкости его. Сечение кольца в форме полукруга дает ббльшую скорость вращения, нежели при прямоугольном сечении. Худшие результаты дает кольцо круглого сечения. При малых числах оборотов употребляют кольцо

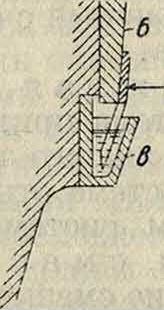
-ф- i 4>-

Фигура 44.

с внутренней насечкой, а при большой вязкости смазки устраивают кольцо с внутренними зубцами, которые захватываются зубцами тонкого пружинного зубчатого кольца, охватывающего вал. По опытам Кранца при окружной скорости на валу в 7,5 м/мин и более диам. кольца следует брать равным 2 диам. вала. При меньших скоростях диам. необходимо увеличивать. Ширина кольца определяется по ф-ле:

b =^з + 8 миллиметров, толщина 3—4 миллиметров, ширина прореза во вкладыше больше на 1,5 миллиметров. Недостатком свободного кольца является зависимость движения его от случайных причин (сгущение масла, неудовлетворительность сцепления с валом,толчки и сотрясения, застревание в прорезе).

Все это устраняется Фигура 45.

при установке кольца, укрепленного на валу. При сравнительно меньшем числе оборотов такая система подачи смазки является вполне надежной. Недостатком же ее является перерезание нижнего загруженного подшипника, что может вызвать сомнение в образовании достаточно прочной пленки и давления внутри масляного слоя, уравновешивающего давление со стороны вала, то есть эта конструкция противоречит основам гидродинамич. теории трения. Лучше перенести кольцо на конец вкладыша, установив над ним ковшик или пластинку а, снимающую масло и подающую его в каналы верхнего вкладыша (фигура 46).

Принудительная смазка эксцентриковыми насосами и смазочными прессами (моллерупами или лубрикаторами), работающими с механическ. приводом от двигателя. Этими приборами смазка подается под давлением преимущественно к закрытым машинным частям и широко применяется в паровых машинах и паровозах, двигателях внутреннего сгорания, компрессорах и тому подобное., причем она может подаваться непосредственно или в распыленном состоянии. От каждого пресса масло должно подводиться лишь к одному месту смазки без разветвления. При нескольких смазочных местах удобнее пользоваться многонасоспы-ми агрегатами. Удобство прямой подачи масла с помощью пресса состоит в том, что при надобности подачу смазки можно значительно усилить. Для усиления смазки распыливанием применяют метод подачи в такт с движением смазываемой детали, например паровой поршень получает смазку в распыленном виде в тот момент, когда он проходит мимо смазочных каналов.

Циркуляционная самотечная смазка применяется преимущественно для стационарных тяжелых и сравнительно быстроходных машин. Эта система состоит (фигура 47) из резервуара а, всасывающего трубопровода б, насоса в, нагнетательного трубопровода г, бака д, расположенного на известной высоте, трубопроводов е_х и е₂> через которые масло подается к местам

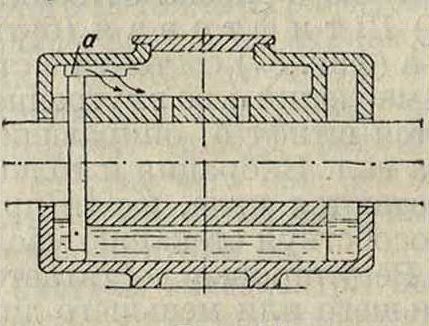
Фигура 46.

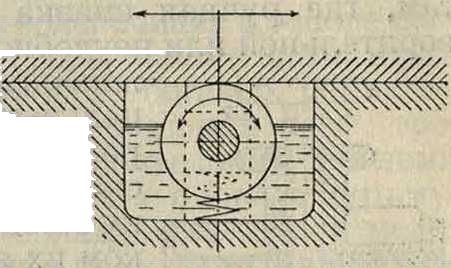
смазки, стока ж, отстойника з, в к-ром осаждаются частицы, загрязняющие смазку, в том числе и частицы металлич. происхождения, камер и, в которых происходит фильтрация смазки, охладителя к, из κ-porb масло поступает в резервуар а, совершив т. о. полный кругооборот. Трубопровод л, сообщающий бак д с резервуаром а, поддерживает постоянный уровень масла. Эта схема м. б. несколько усложнена установкой насоса, работающего от электромотора независимо от двигателя, что необходимо для машины с длительным разбегом и остановкой. При многоцилиндровых машинах устанавливаются также параллельно работающие насосные агрегаты (лубрикаторы). Для маломощных машин при незначительном развитии тепла и малой засоряемости смазки схема может несколько упрощаться: холодильник

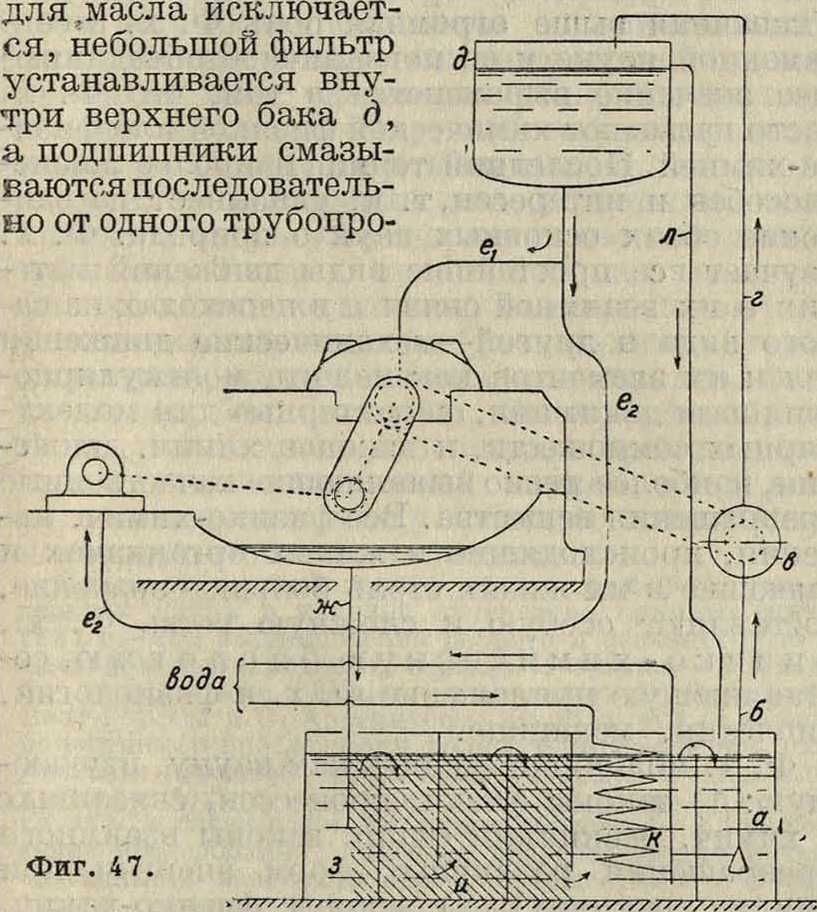
вода, что сокращает его длину. Если несколько машин работает рядом, то их обслуживают одним баком, создавая гидростатич. давление столбом смазочного материала.

Циркуляционная смазка под давлением употребляется там, где необходимо хорошее наполнение подшипников как в целях безусловной жидкостной смазки, так и в целях промывания их от продуктов износа, а гл. обр. для охлаждения подшипников в тех машинах, где развивается относительно высокая t°. Система смазки этого рода употребляется в двигателях внутреннего сгорания, в паровых турбинах, в судовых машинах с сильно нагруженными осевыми и упорными (гребенчатыми) подшипниками. Смазка под давлением может применяться лишь там, где подшипники совершенно закрыты; при этом должны приниматься меры к полному улавливанию стекающего масла. Давление в трубопроводах достигается при помощи зубчатого или ротационного насоса. В паровых турбинах главный масляный насос а {фигура 48) соединен червячной передачей с валом турбины. Т. к. насос начинает подавать смазку под достаточным давлением лишь после достижения турбиной 7₃ нормального числа оборотов, то в этой системе смазки необходим вспомогательный масляный насос б со своим вспомогательным фильтром в Циркуляционный путь смазочного масла таков: из отстойного резервуара е через главный фильтр д масло поступает в главный насос а; оттуда по. трубопроводу, на к-ром установлен редукционный клапан е, в маслоохладитель oie, из κ-poro распределяется по подшипникам турбины и генера

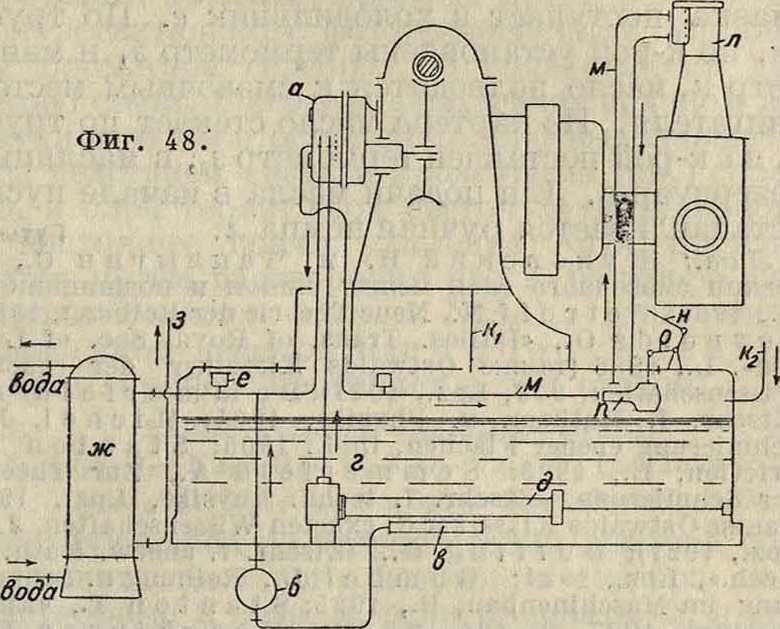
тора по маслопроводу з. Масло возвращается в резервуар по трубам к_г и к₂- В современных Турбинах система смазки непосредственно связана с системой регулирования, которая управляет сервомотором, приводящим в движение дроссельный клапан турбины. При понижении давления в главной циркуляционной системе регулятор воздействует через трубопроводы системы регулирования на поршень сервомотора, к-рый, перемещаясь, прекращает доступ пара в турбину. Т. о. турбину невозможно будет пустить в ход, пока не установится достаточное движение в трубопроводах, распределяющих смазку по подшипникам, и тем самым устраняется всякая возможность повреждения их вследствие недостаточной подачи смазки к ним. На фигуре 48 сервомотор л связан трубой м с главным масляным насосом. Регулятор через тягу н и рычаг о воздействует на клапан п, к-рый выпускает масло из системы регулирования в том случае, когда давление в смазочной системе недостаточно; поршень сервомотора при этом перемещается, закрывая доступ.

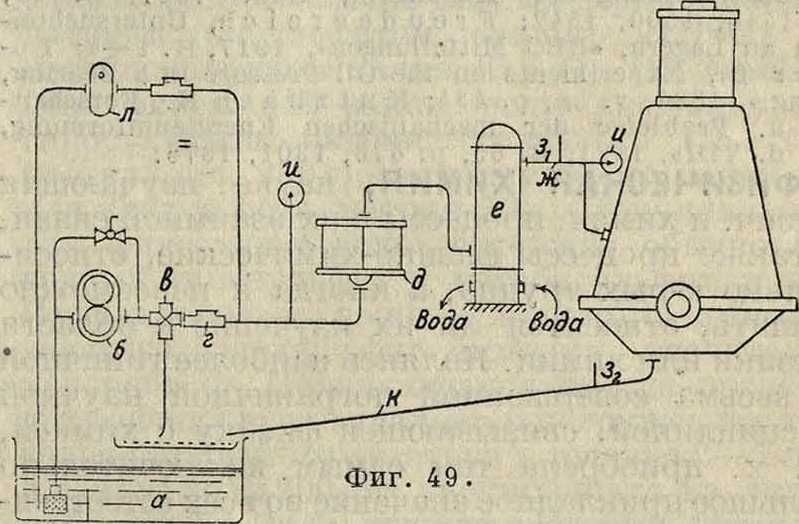
пара в турбину. Т. к. для управления сервомотором требуется - сравнительно высокое давление (2,5—4 atm), то в нек-рых системах турбин устанавливают два насоса: один высокого давления, подающий масло в систему регулирования, другой—низкого, питающий систему смазки. В последней системе давление не должно превосходить удельного давления в осевых и упорных подшипниках турбогенератора. Циркуляционная система смазки под давлением для поршневого двигателя, рекомендуе-

мая Фальцем, указана на фигуре 49. Из маслоотстойного резервуара а масло засасывается зубчатой помпой б, снабженной перепускным краном, и направляется через предохранительный вентиль в и обратный клапан г к сдвоенному с переключением фильтру б, минуя к-рый смазка поступает в холодильник е. По трубе ою, по которой установлены термометр з_г и манометр и, масло подводится к смазочным местам двигателя. Из картера масло стекает по трубе к, на которой поставлен термометр з₃, в масляный резервуар а. Для подачи масла в начале пуска устанавливается ручная помпа л. гутьяр.

Лит.: Жуковский Н. и Чаплыгин С., О трении смазочного слоя между шипом и подшипником, М., 1904; PetroffN., Neue Theorie der Reibung, 1887; Reynolds О., «Philos. Trans, of Royal Soc. of London», L., 1886 (также Ostwalds Klassiker der exacten Wissenschaften, 218, Lpz., 1927); Sommer fe Id A., «Ztschr. f. Mathem. u. Physik», 1904; Michel, Die Schmierung ebener Flachen, ibid., 1905; Stanton T., Friction, L., 1923; Sommerfeld A., Zur Theorie der Schmierung, «Ztschr. Г. techn. Physik», Lpz., 1921 (также Ostwalds Klassiker d. exacten Wissenschaften, 218, Lpz., 1927); Duffing G., «Ztschr. f. angew. Math. u. Mech.», Lpz., 1924; Griimtel L., Reibung u. Schmierung im Maschinenbau, B., 1925; Stanton T., «Engineering», 1927, y. 124, p. 312; I-Iodgkinson Fr., ibid., 1929,У. 128, p. 690; Charnok G., ibid., 1929, v. 128, p. 801; Duffing G., Handbuch der physikal. u. techn. Mechanik, hrsg. v. F. Auerbach u. W. Ilort, B. 5, p. 839, L z., 1931; Bradford, «Trans, of the Am. Soc. of Mechanical Eng.», N. Y., 1931, v. 53, 11, p. 71; Kingsburg, ibid., 1931, 11, p. 59; Lubrication Research Activities, ibid., 1931, 11, p. 22 (обширный указатель литературы); В ii c he, «Z. d. VDI», 1932, 9; Reye T., Zur Theorie der Za fenreibung, «Zivilinge-nieur», 1860, B. 6, p. 235—254; Stribeek R.,Diewe-sentliche Eigenschaften der Gleit- u. Rollenlagen, «Z. d. VDI», 1902, B. 46, p. 1 341, 1432, 1 463; Lasche O., Die Reibungsverhaltnisse in Lagern mit hoher Umfangsge-schwindigkeit, ibid., 1902, B. 46, p. 188 1, 1 932, 1 961; Lasche 0.,Der Dampfturbinenbau derAllgemeinen-Elek-Irizitats-Gesellschaft, Berlin, ibid., 1906, В. 50, p. 1 355; Lasche· О. u. Kieser W., Konstruktion u. Material im Bau von Dampfturbinen u. Turbodynamos, B., 1925; C h a r p y A., Versuche iiber die zur Verminderung der Reibung dieneden Metallegierungen, «Z. d. VDI», 1898, B. 42, p. 1300; Eam merer О., Entstelmng der Lagerversuche, Mch., 1920; A s c h e r R., Die Schmiermit-tel, ihre Art, Priifungu. Verwendung, B., 1922; Falz E., Grundzoge der Schmiertechnik, B., 1925; 1farr A., Die Turbinen fiir Wasserkraftbetriebe, B., 1912; L en z K., Die Schmierung schnellaufender Maschinen, «Z. d. VDI», 1907, B. 51, p. 855; Turk C., Walzenlagerung, «St. u. E.», 1927, n. 1437; Stribeek R., Kugellager fiir be-liebige Belastung, «Z. d. VDI», 1901, b.45, p. 73, 118; Stribeek R., Priifverfahren fur geharteten St.ilil u. Beriicksichtigung der Kugelform, ibid. 1907, B. 51, p. 1445, 1500, 1542; F r e u d e n r e i c h, Untersuchun-gen an Lagern, «BBC Mitteilungen», 1917, Η. 1—4; Tower B., Experiments on the Oil Pressure in a Bearing, «Eng.», 1 884, v. 58, p. 434; Kutzbach K., Forschrit-te u. Probleme der mechanischen Energieumformung, «Z. d. VDI», 1921, B. 65, p. 673, 1301, 1376.