> Техника, страница 90 > Фотохимия

Фотохимия

Фотохимия, учение о химич. действиях света.· Ф. является одной из самых молодых областей знания и как научная дисциплина насчитывает сто с небольшим лет. Это объясняется тем, что в течение долгого времени наиболее известные фотохимии, реакции (фотосинтез в растении, выцветание красок на солнце) приписывали не свету, но теплоте солнца. Начало количественному исследованию фотохимии. процессов положено работами Гротгуса (1817 г.) и затем Дрепера (1841—1845 гг.), впервые сформулировавших закон, согласно к-рому химически действуют только те лучи, которые поглощаются веществом. С другой стороны, Бунзен и Роско (на основании исследований фотохимии. образования НС1 из газообразных Н₂ и С1₂) установили связь между количеством превращенного вещества и количеством падающей лучистой энергии. Согласно закону

9

Бунзен а-Р о с к о фотохимии, действие будет одно и то же, если произведение интенсивности падающего света на время его действия постоянно, то есть если свет разной интенсивности Jj и J₂ действовал в течение различных промежутков времени t_x и t₂, то эффект будет одинаков, если J_xi₁₌= J₂t₂. Поскольку в законе Бунзена-Роско речь идет о падающей интенсивности и не учитываются возможные изменения абсорбции в течение самой реакции, применимость его ограничена, и в целом ряде случаев наблюдаются заметные отступления от этого закона. В начале 20 в (Вант-Гофф, 1904) в качестве обобщения законов Гротгуса-Дре-пера и др.было высказано предположение о том, что фотохимический эффект определяется полным количеством поглощенной энергии. Это предположение было подвергнуто экспериментальной проверке, причем впервые были применены точные физические методы (Лютер, Вейгерт, Лазарев), и получило полное количественное подтверждение для случая, когда реакция идет в одной полосе поглощения. Однако начало пониманию внутреннего механизма фотохимии. процессов было положено тогда, когда было понято, что Ф. есть проблема теории квантов (смотрите). Истинным основным законом Ф. является фотохимии, закон эквивалентности (Эйнштейн, 1912), связывающий количество прореагировавших молекул с числом поглощенных световых квантов. Быстрое развитие теории молекулярных спектров, последовавшее за возникновением теории атома Бора, позволило уже в самое последнее время (Франк, 1926) окончательно понять природу элементарного фотохимии, процесса.

Независимо от общей Ф. развивалась научная фотография; к пониманию природы т. н. скрытого изображения удалось прийти лишь в самое последнее время благодаря чисто физич. работам над фотопроводимостью кристаллов.

Фотохимии, закон эквивалентности. Процесс поглощения света согласно современным представлениям сводится к поглощению отдельными молекулами целых квантов излучения, так что не все молекулы в результате поглощения получают избыток энергии, но только нек-рые. Величина этого избытка энергии весьма значительна: так, поглощение квантов фиолетовых лучей (Я=4 000а) эквивалентно сообщению энергии ~80 Cal на моль. Очевидно, что число молекул, получивших такую избыточную энергию, как-раз равно числу поглощенных световых квантов. Поэтому если в результате поглощения света происходит фотохимии, реакция, то число первичных фотохимии, процессов должен быть равно числу поглощенных световых квантов. В этом и заключается фотохимии, закон эквивалентности (Эйнштейна), к-рый т. о. является простым следствием квантовой природы поглощения. Экспериментальное изучение квантовых выходов, то есть числа прореагировавших молекул на один поглощенный квант, показало (Э. Варбург), что в то время как для значительного числа реакций величина квантового выхода близка к 1, как это должен быть по закону Эйнштейна, существует много реакций, где этот закон кажущимся образом грубо нарушается. Так например, при фотохимии, реакции Н₂ + С1₂=2НС1 на 1 поглощенный квант приходится до 10⁵ образующихся молекул HG1. Отступления происходят вследствие того, что при фотохимии, реакциях вслед за первичным процессом весьма часто следует ряд вторичных. Если при этом цепь вторичных процессов обрывается быстро, квантовый выход выражается небольшим числом (2—3); в отдельных же случаях получаются весьма длинные цепи, и квантовый выход достигает огромной величины (смотрите ниже).

Элементарные фотохимии, процессы в газах. Фотохимии, закон эквивалентности дает определенный критерий наличия или отсутствия вторичных процессов, следующих за первичным. Зная квантовый выход и кинетику реакции, можно сделать заключение об ее механизме, но природа самого первичного процесса м. б. раскрыта лишь путем изучения спектра абсорбции реагирующего вещества. Проблема состоит в следующем. Если молекула поглощает квант света, то каков непосредственный результат этого поглощения: происходит ли непосредственно вслед за ним спонтанный распад молекул на более простые части или же возбужденная молекула должна испытать еще последующее соударение, для того чтобы произошел распад? Ответ на этот вопрос сделался возможным благодаря успехам в изучении т. н.полосатых, или молекулярных, спектров (смотрите). Рассмотрим простейший случай двухатомной молекулы. Согласно условию частот Бора испускание и поглощение света происходит только при переходах между двумя стационарными энергетич. состояниями, причем кг_тп=Е_т—Е_п,ткеЕ_т и Е_п—энергии соответственных состояний. Первая задача сводится к отысканию возможных энергетич. состояний молекулы. Энергия молекулы Е, вообще говоря, м. б. представлена как сумма трех слагаемых: электронной энергии Е_е, энергии колебаний ядер, образующих молекулу E_v, и энергии вращения молекулы как целого Е_г:

Е — Е_е + E_v + Е_г

E_eyE_vy Е_г.

Энергия вращения молекулы как целого в простейшем случае вполне симметричной электронной оболочки (состояние *Σ) сводится к энергии вращения одних только ядер и м. б. точно вычислена при помощи волновой механики:

E_r=K(K +1)™ =К(К + 1)В, где К—квантовое число вращения—целое число, равное

fa,ч

0, 1, 2.; J—момент инерции, а В=——. Если мы по-

’ bn^J

ложим, что при возбуждении молекулы изменяется только одна энергия вращения, то есть АЕ_е=ΔΕ_ν=0, то мы получим т. н. ротационный спектр. Частоты АЕ АЕ„

= уг ^ 1Г ’ ^{Е0 АЕг =} + ^±)-К"{К" + 1)] В.

При помощи квантовой механики можно показать, что не все мыслимые переходы между различными состояниями вращения возможны, но только такие, при которых К изменяется на единицу, то есть К-К"=АК=± 1. Имея это в виду, получим

АЕ_Г=2( К + 1) В=2 М В, где М=К + 1=1, 2, 3.

И следовательно

”=^2М8^7’ "-¹· ²’³·--

то есть чисто ротационный спектр должен состоять из ряда равноотстоящих линий. Т. к. АЕ_Г имеет относительно весьма малые значения (порядка cal), то v_r также имеют малые значения, и весь спектр лежит в далекой инфракрасной части. Такие спектры действительно известны и промерены,напримерв случае газообразных HF, НС1, НВг, Н J (Черни). Т. к. изменения энергии вращения ограничены Правилом отбора (АК=± 1), то эти изменения слишком малы, чтобы можно было ожидать в результате их каких-либо фотохимич. превращений.

Энергия колебаний. С грубым приближением можно рассматривать молекулу как гармонический вибратор, механич. моделью которого могут служить два шара, соединенные упругой Пружиной. Для такого вибратора сила, возвращающая шары к их положе-

нию равновесия, пропорциональна элонгации F=- Ах; /—постоянная квазиупругой силы, а частота колебаний вычисляется по известной из механики формуле ω =

где μ—приведенная масса: -=——i——. Энергия гар-μ т _л т_в

монич. вибратора м. б. вычислена по квантовой механике:

2л У μ

Ε_ν=^ hco, υ=0, 1, 2, 3.

Заметим, что при ν=0 получается Ε_ν=^ Ηω, то есть квантовая теория требует существования «нулевого колебания»=-i hco. Частота, излучаемая или поглощаемая молекулой—гармония, вибратором,

ΊΓ “ [(»^/+|)-(” + |)]“=(”^,-»^//)“·

Т. к. здесь также имеет место «правило отбора» Δ®=± 1, то ν «= со, то есть частота колебаний такой молекулы должен быть равна частоте колебаний мехайич. модели. На самом деле однако допущение гармоничности колебаний молекулы б. или м. отвечает действительности лишь при малых значениях ν, то есть при малых амплитудах колебаний. По мере усиления колебаний сила связи в молекуле все в большей степени будет отличаться от квазиупругой. При больших амплитудах связь расслабляется и в конце концов становится равной нулю—молекула диссоциирует. Мы можем с известным приближением, к-рое оказывается во многих случаях вполне достаточным, принять, что отступление от гармоничности—степень ангармоничности—пропорционально квантовому числу ν +, то есть что

= +!) ^ho> f¹-* (® + ^)]=^ι“[(^ο + ΐ)-^α (^{К +} У1

где x—фактор ангармоничности. Из этого ур-ия следует, что по мере усиления колебаний (увеличение ν) разность между соседними значениями энергии убывает. Т. о.

, если мы построим схему уровней колебательной энергии, то получим последовательность, изображенную на фигуре 1, где видно, что соседние уровни по-Ll-li-U-l.l LL-. степенно сближаются вплоть

;.. до Полного слияния. Послед-

: ----р нему отвечает случай, когда

-6 сила связи между атомами ста-

-новится равной нулю, то есть мо-

__₄ лекула перестает существо-

_Λ вать как целое—она диссоци-

^ 3 ирует. Очевидно, что высота

___2 этого места слияния над нулевым уровнем равна энергии --- диссоциации. В нек-рых случаях Подобная схема колеба-

____п тельных уровней м. б. Пол-

“ ностью построена на основа-Фигура 1. нии изучения молекулярного спектра. В таких случаях имеется возможность спектроскопически определить столь важную термохимии, константу, как энергия диссоциации. Если же полную схему построить не удается, то все же По ходу первых уровней энергии можно найти их зависимость от квантового числа ν и затем экстраполировать место слияния, то есть опять-таки найти энергию D, хотя уже с меньшей точностью. В области, расположенной выше места слияния, молекула перестает существовать как целое. В этой области условие квантования теряет свою силу: независимые атомы могут двигаться с любыми значениями поступательной кинетич. энергии, т. к. последняя не подлежит квантовым ограничениям. Пока молекула ведет себя, как гармония, вибратор (при малых г;), соблюдается правило отбора Δυ=±1, то есть переходы возможны только между соседними уровнями, и молекула излучает или поглощает только одну основную частоту ν=ω; частоты, отвечающие «обертонам»—2ω, 3ω, невозможны. Для больших значений ν гармоничность нарушается, и правило отбора падает; вместе с тем появляются линии «обертонов». Однако интенсивность их мала и чрезвычайно быстро убывает, что указывает на малую вероятность переходов А и > 1. Отсюда следует, что распад молекулы путем одного только накопления колебаний (без одновременного электронного перехода) практически мало вероятен.

Электронная энергия является наибольшим по величине слагаемым в сумме Е_е + E_v + Е_г. Электронные уровни молекулы могут образовывать такие же последовательности, как и электронные уровни атома. На самом деле для большинства молекул известно лишь весьма небольшое число таких уровней. Электронная энергия характеризуется квантовыми чи, из которых важнейшим является А, аналогичное квантовому цислу

*/////////,					щш.
					D
					А? D
					-ϋ,
	ί /	A			В У/////А
					А
					*7 я
					Аг А
					А А

L орбитального момента у атомов, но отличающееся от него тем, что Λ представляет собою проекцию орбитального момента на электрическую ось молекулы (прямую, соединяющую ядра). Подобно тому как в зависимости от величины L (0, 1, 2 .) у атомов различают S-, Р-, П-тррмы, в случае молекул значениям А=0, 1, 2. отвечают различные серии термов, которые здесь обозначаются как Σ-, Я-, А-. термы. Переходы между различными термами регулируются правилами отбора, а именно ΔΑ м. б. равно 0 или ± 1, то есть возможны переходы Σ — Σ, П — П или Σ — П и т. д. (см Спр. ТЭ, т. IX, стр. 112 и 132).

Пусть А (фигура 2)—уровень с нулевым колебанием (-г;=0) при нормальном состоянии, В— такой же уровень при возбужденном состоянии электронной оболочки. Над каждым из электронных уровней А и В расположен еще ряд колебатель-ныхуровней^!, А₂,. В_1УВ₂,.

Поэтому при поглощении света возможны не только переходы между А и Б, но еще и переходы АВ_и АВ₂,. Т. о. вместо одной линии мы получим уже целую последовательность их.

Но между каждыми двумя соседними колебательными уровнями лежит еще целая серия гораздо более тесно расиоло- ^{фиг 2}· женных вращательных уровней, к которым также возможны переходы. Эти последние в еще большей степени усложняют спектр, так что вместо каждой линии, отвечающей переходу между определенными колебательными уровнями, получаются полосы, состоящие из большого числа очень тесно расположенных линий и часто имеющие с одной стороны резкий край или кант. Вследствие значительной разницы в величине отдельных слагаемых энергии молекулы (Е_е > E_v > Е_г) мы получаем следующую градацию: электронный переход определяет область длин волн, где расположен весь спектр; переходы между колебательными уровнями создают последовательность полос, и наконец переходы между вращательными уровнями обусловливают тонкую структуру каждой отдельной полосы. Колебательные уровни верхнего состояния, так же как и уровни нижнего состояния, сближаются до полного слияния, отвечающего диссоциации возбужденной молекулы.

Фотохимические реакции возбужденных атомов и молекул. В предыдущем мы рассматривали исключительно такие случаи, где переходы происходят между дискретными энергетич. состояниями; атом или молекула, возбужденные до одного из таких дискретных энергетич. уровней, обладают способностью пребывать в этом возбужденном со стоянии в течение заметного промежутка времени. Разнообразные экспериментальные методы позволяют непосредственно определить это «время задержки», обычно обозначаемое через т. В большинстве случаев т равно 10^-8-f- 1СГ⁷ ск.; реже наблюдаются более значительные величины т(например для возбужденного N0₃ т=10^-5ск.). В масштабе внутриатомных (молекулярных) процессов эти промежутки времени имеют огромную величину: достаточно указать, что за 1СГ⁸ ск. молекула успевает совершить 10⁵ колебаний. Если газ достаточно разрежен, то по истечении времени т молекула спонтанно возвращается в нормальное состояние, отдавая свой избыток энергии вновь в виде света (флуоресценция газов). При этом оказывается, что количества энергии, которые молекулы

*9

могут таким путем поглощать и испускать, сохраняя свою целостность, могут значительно превосходить их энергию диссоциации. Так, молекула J₂ при освещении линией Л=1 849 А (далекий ультрафиолет) дает типичный молекулярный спектр флуоресценции, свидетельствующий о сохранении молекулы как целого несмотря на то, что избыток энергии, которым обладает при этом возбужденная молекула J₂, в пять раз превосходит энергию ее диссоциации. Таким образом при достаточно низком давлении выход флуоресценции равен 100%, а фотохимии, выход равен нулю. Но возбужденные молекулы, обладающие столь значительными избытками энергии, обладают и повышенной способностью к химии, реакциям. Если примешать к разреженному газу какой-нибудь другой газ, то интенсивность флуоресценции, вообще говоря, убывает («гашение флуоресценции»), но вместе с тем во многих случаях наблюдается фотохимии, реакция. Естественно представить, что те из возбужденных молекул, которые за время т не испытают соударения, возвратятся в нормальное состояние спонтанно, отдавая избыток энергии в виде излучения флуоресценции; те же, которые в возбужденном состоянии соударяются с посторонними молекулами, могут затрачивать свой избыток энергии на химическую реакцию и в этом случае излучения не дадут. — Простейшей фотохимической реакцией этого типа является например реакция между возбужденными атомами Hg и молекулами 0₂. При освещении разреженных₀паров Hg монохроматическим светом Я=2537 А наблюдается интенсивная флуоресценция с испусканием той же линии Я=2537А(резонансное излучение);если же примешать к парам Hg кислород, то флуоресценция сильно ослабляется, а вместе с тем начинает идти реакция с образованием HgO. Нетрудно видеть, что только в предельном случае достаточно высокого парциального давления примешанного газа каждая возбужденная молекула в течение времени г испытает соударение^, ведущее к реакции. В этом случае квантовый выход будет равен 1 [если не происходит цепной реакции (смотрите)]; если же давление низко, то часть возбужденных молекул вернется в нормальное состояние (с испусканием света), и квантовый выход будет <1. Итак, для случая, когда первичный процесс сводится к возбуждению, возможны сколь-угодно малые квантовые выходы, и кроме того квантовый выход должен сильно зависеть от давления.

Наряду с обычными возбужденными состояниями, для которых τ^ΗΓ⁸, известны и т. н. метастабильные состояния, где τ может достигать относительно огромных значений от 10² ск. и даже до нескольких ск. Ясно, что в этом случае квантовый выход даже при низких давлениях должен в огромной степени возрастать. Замечательным примером таких состояний является недавно открытое метастабильное состояние молекулы О ₂ (состояние ¹Σ), где τ достигает 7 ск.; энергия возбуждения для этого состояния равна 37 Cal, и следовательно все реакции, где тепловой эффект меньше или равен этой величине, могут легко возбуждаться молекулами 0₂ в этом метастабильном состоянии. Повидимому оно играет большую роль в фотохимическом разрушении озона в верхних слоях атмосферы.

Возбужденные атомы и молекулы могут давать начало фотохимич. реакции, не только вступая в реакцию сами, но также путем передачи энергии другим молекулам посредством ударов второго рода. При этих ударах возбужденная молекула возвращается в нормальное состояние без излучения и весь свой избыток энергии передает соударяющейся частице. Самый простой случай здесь состоит в том, что последняя при этом увеличивает свой запас кинетич. энергии. Результатом этого явился бы переход энергии возбуждения в энергию хаотических тепловых движений. Опыт и теория согласно показывают однако, что такое использование энергии возбуждения на самом деле происходит с весьма малой степенью вероятности. Гораздо вероятнее передача энергии тогда, когда соударяющаяся частица может использовать значительную часть получаемой энергии, для того чтобы в свою очередь перейти в возбужденное состояние. Может случиться при этом, что, получив таким путем избыток энергии, частица отдаст его в виде излучения — сенсибилизированной флуоресценции; в других случаях частица под влиянием полученной энергии может вступить в реакцию с какой-нибудь другой частицей или сама испытать распад. Во всех случаях этого типа происходит т.н. сенсибилизированная фотохимич. реакция. Наиболее типичными сенсибилизаторами являются₀ атомы Hg: при поглощении света с Я=2 537А они приходят в возбужденное состояние (³pt) с избытком энергии ~Ί10 Cal на моль. Если в смеси с парами Hg имеются пары Cd, то при соударении с Hg* (звездочка указывает на возбужденное состояние) атомы Cd возбуждаются и начинают флуоресцировать, хотя в отсутствие Hg пары Cd в этой области совсем не поглощают света и следовательно не могут флуоресцировать. Это—типичный случай сенсибилизированной флуоресценции. Если же к ртутному пару примешан₀ водород, то при освещении той же Я=2 537А наблюдается диссоциация Н₂:

Hg+/iv=Hg“; Hg*+H₂=2H + Hg, хотя часть атомов реагирует по схеме:

Hg+h^Hg“; Hg* + H₂=HgH + H.

Известен и ряд других реакций возбужденных атомов Hg: в смеси Н₂ 4- 0₂ под влиянием освещения в присутствии Hg происходит образование воды при комнатной $°; наблюдались также многочисленные реакции углеводородов в присутствии Hg“. Вероятность передачи энергии при таких процессах тем больше, чем меньшая часть энергии идет при этом на увеличение кинетической энергии молекул и следовательно чем большая ее часть превращается в энергию возбуждения. Мы имеем здесь дело со своеобразным резонансным эффектом, к-рый проявляется весьма резко. Так, при флуоресценции паров Na, сенсибилизированной Hg, в спектре флуоресценции подавляющая часть интенсивности приходится на линию, отвечающую переходу 7²$ — 2²Р; но как-раз этому переходу отвечает энергия (4,880 V), весьма близкая к энергии возбуждения атома Hg(³Pi)^=4,860 Y. Подсчет расстояний,-на которых происходит передача энергии при условии резонанса, показывает, что расстояние это всегда значительно (иногда в сотни раз) превосходит величину радиуса молекулы, вычисленную на основании кинетич. теории газов. Причина появления повышенных эффективных радиусов передачи энергии при резонансе разъяснена при помощи волновой механики.

Фотохимические изменения связей. Близкими к рассмотренному типу первичных фотохимии, процессов являются реакции, в которых изменяется характер связей. Одним из наиболее замечательных новых результатов спектроскопии сложных молекул является возможность решения вопроса о том, имеем ли мы дело с простой, двойной или тройной связью; характерной для вида связи является величина К, определяемая из ур-ия

2πω=у^ГЩ-,

где со—частота механических колебаний, а I— момент инерции. Обе эти величины определяются путем анализа молекулярных спектров: первая — путем исследования последовательностей кантов, вторая—путем анализа тонкой структуры полосы. Оказывается, что в веществах с двухатомной молекулой (углерод, азот, кислород) значения К в самых разнообразных соединениях с простой, двойной и тройной связями весьма близки соответственно 27ν, 54*> и Ί9ν, то есть почти точно относятся, как 1 : *2 : 3. Вместе с тем частоты колебаний во всех случаях весьма близки к одним и тем же средним значениям: для тройной связи×i X—2 200, для двойной —×: X—1 650 и для простой —×·×~ 1 000. Бели выбрать три молекулы с одинаковым числом электронов: N₂, СО и С₂Н₂, то они обнаруживают поразительную аналогию—все три в нормальном состоянии обладают двойной связью, и т. к. у них кроме того электронные оболочки имеют замкнутый характер, то в нормальном состоянии все три являются инертными в химическом отношении. Однако анализ спектров этих молекул показывает, что в возбужденном состоянии тройная связь заменяется двойной (со изменяется от 2 200 до 1 700), вместе с тем одна связь освобождается, и молекула приобретает способность легко реагировать. Т. о. известная реакция окисления ацетилена в формальдегид (по Мекке) м. б. истолкована сл. обр.:

1 НС ΞΞ СН + hv -► нс=СН;

н н

1 НС : СН 4- о =и О -> НС=СН -+ С — С -> Н₂С — О 4- СО ‘ * * * ‘_п— λ # % формальдегид

^u О О

глиоксаль

Аналогичное явление имеет место в случае молекул с двойной связью: 0₂, Н₂СО, С₂Н₄. Здесь в результате абсорбции света двойная связь заменяется простой, и молекулы опять-таки приобретают повышенную способность к реакции. Как известно, двойные связи играют большую роль в химии красителей: именно они являются «хромофорными» связями. Т. о. анализ молекулярных спектров приводит к выводу, что краска устойчива к свету тогда, когда абсорбция не изменяет характера ее связей.

Оптическая диссоциация, фотодиссоциация, важнейший тип элементарных фотохимических процессов, при котором возбужденная молекула спонтанно, то есть без последующего соударения, распадается на атомы или вообще на составляющие ее части. Механизм таких процессов выяснился благодаря изучению молекулярных спектров. Для понимания этого механизма необходимо ознакомиться с одним удобным вспомогательным приемом, получившим за последнее время широкое применение, — с методом рассмотрения при помощи потенциальных кривых.

Потенциальная кривая изображает зависимость потенциальной энергии молекулы от расстояния между ее ядрами. Очевидно, что образование устойчивой молекулы из атомов возможно только в том случае, когда потенциальная энергия U(r) при нек-ром расстоянии атомов г_е имеет минимум, отвечающий устойчивому равновесию. Разложим U(r) в ряд по степеням смещения г—т_е:

Ь^т(г)=и₍г₄) + (г-г.)(§)_г„_г.+

, (r-r_g)^a (d*U,

^ 2 * [dr* )r=r_e ^ ··*

Если смещение мало, то в этом ряде можно ограничиться написанными членами и отбросить все члены с высшими степенями (т — т_€). Принимая за нуль потенциальной энергии то ее значение, при к-ром ядра находятся в равновесии, получим U(j_f)=0, а т. к. при г=получаем минимум потенциальной энергии, то л

Отсюда

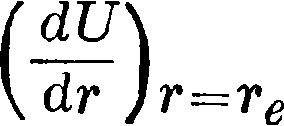
= 0.

^:

где ξ =т — т_е. На основании соотношения между силой и потенциалом получимF— ^=—2 Τζξ.

Т. о. для малых смещений мы всегда можем принять, что сила пропорциональна смещению, то есть что колебания гармонические, и т. к. в этом случае U=άξ², то кривая потенциальной энергии будет параболой (фигура 3). На самом деле однако это будет _иверно только для г, близких к г_е. По мере возрастания г сила увеличивается не беспредельно, но возрастает до некоторого максимума, после чего начинает убывать, падая до нуля, когда атомы раздвинуты настолько, что связь между ними нарушается, и молекула диссоциирует. Но при этих условиях отбрасывание высших членов ряда становится недопустимым, и формула, выражающая зависимость U от смещения, приобретает более сложный вид. Мы можем однако легко установить качественно ход кривой потенциальной энергии.· Так как сила связи при некоторой величине смещения начинает ослабляться, то кривая U(r) в сторону возрастающих г поднимается медленнее, нежели парабола, затем проходит через точку перегиба и наконец идет параллельно оси абсцисс, когда связь между атомами нарушается. Наоборот, влево от реальная кривая идет круче, нежели парабола, вследствие чрезвычайно быстрого возрастания отталкивательных сил на малых расстояниях (фигура 4). В нормальном, невозбужденном состоянии молекулы атомы покоятся на расстоянии г_е. Если мы их раздвинем или сблизим, то появится сила, тянущая их обратно к положению равновесия. Под влиянием этой силы молекула придет в колебание, причем изменение потенциальной энергии при этом колебании наглядно будет представляться потенциальной кривой молекулы. Если мы себе представим, что один из атомов закреплен в начале координат, то другой будет

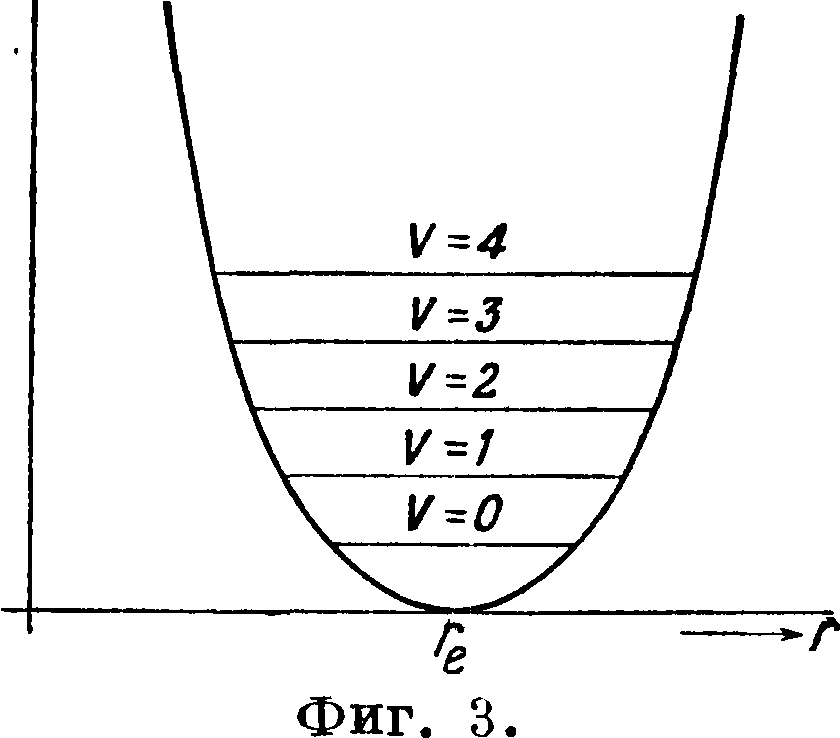
колебаться так, как колеблется под действием силы тяжести шарик, положенной в чашу, сечение которой имеет форму потенциальной кривой.

Мы знаем однако, что колеблющаяся молекула не может обладать любым запасом энергии колебаний, но только определенными количествами этой энергии, образующими дискретный ряд. Эти возможные значения энергии образуют лестницу уровней (фигура 1 и 2). Весьма удобно комбинировать потенциальную кривую со схемой уровней (фигура 3 и 4). С точки зрения классическ. физики описанные взаимодействия между атомами, ведущие к образованию молекулы, являются единственно возможными. Новая квантовая механика показала однако, что два атома водорода при сближении взаимодействуют по потенциальной кривой I (фигура 5) лишь в 25% из числа всех возможных случаев; в 75% случаев они взаимодействуют по кривой II, вовсе не имеющей минимума. Так как эта последняя кривая при уменьшении расстояния монотонно идет вверх, то это значит, что атомы на всех расстояниях отталкиваются. Возможность такого рода взаимодействий, подтверждаемая многочисленными спектроскопическими фактами, не ограничивается водородными атомами. Очевидно, что при взаимодействии по кривой II устойчивая молекула вообще не может образоваться, и следовательно при переходе с кривой типа I На кривую типа II уже существовавшая молекула должна испытать распад. Существованием таких кривых объясняется фотохимический распад в целом ряде случаев.

Потенциальными кривыми можно воспользоваться при рассмотрении механизма элементарных фотохимии, процессов. Непосредственным результатом поглощения квантов видимой

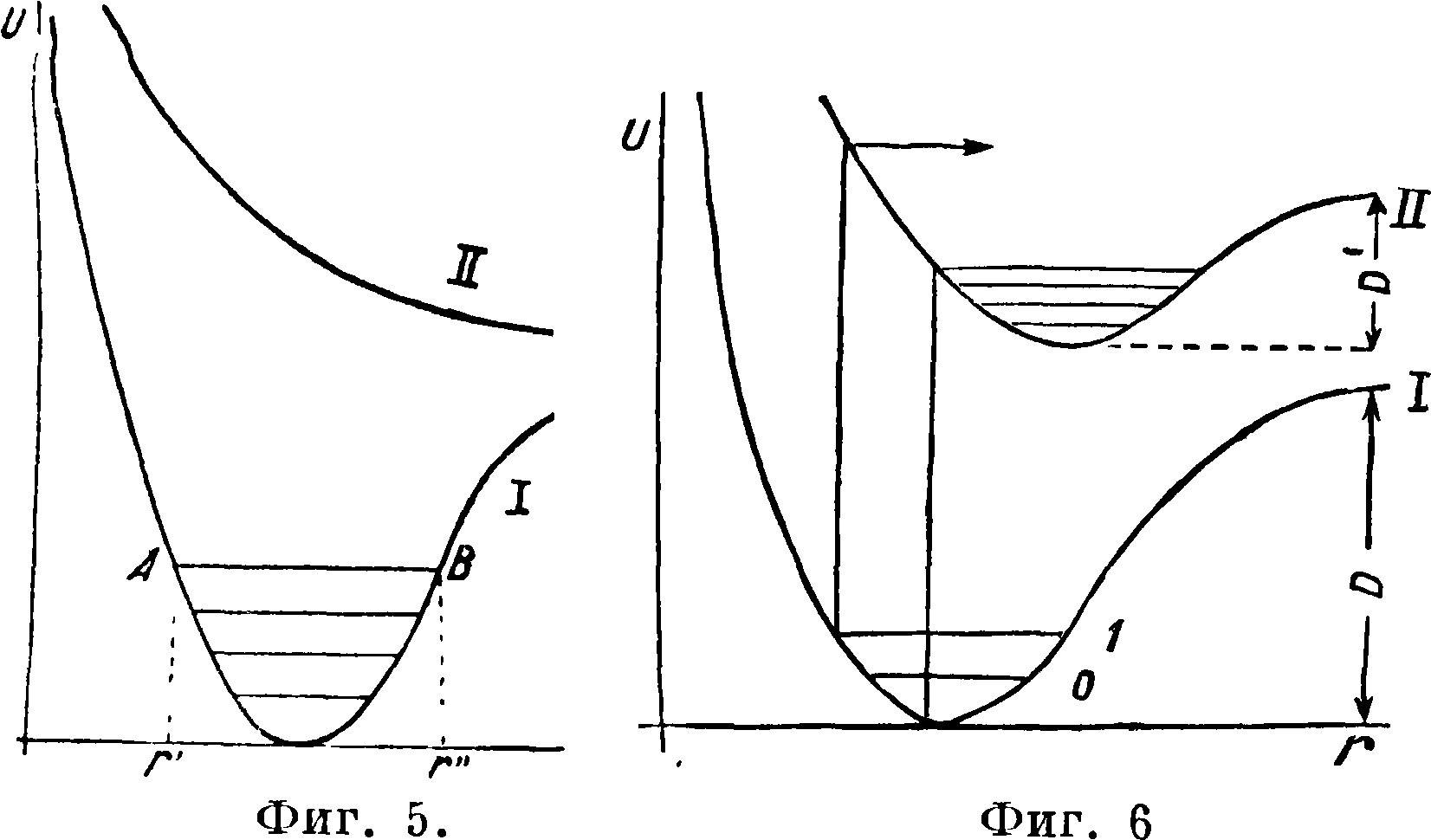
или ультрафиолетовой части м. б. только возбуждение электронной оболочки. Между тем распад молекулы всегда является следствием колебаний ее ядер. Объяснение того, каким образом происходит передача части электронной энергии колеблющимся ядрам, дал Франк: электронное возбуждение есть весьма быстрый процесс, т. ч. значительно более тяжелые ядра в момент, когда электронный переход уже завершен, еще сохраняют прежнее положение равновесия; но возбуждение электрона как правило резко изменяет условия равновесия в моле куле; в результате ядра, находившиеся в момент поглощения в равновесии, после перехода приобретут избыток потенциальной энергии и начнут совершать колебания около нового положения равновесия. Рассуждение приобретает особую ясность, если воспользоваться потенциальными кривыми: на фигуре 6:1—потенциальная кривая нормального состояния, II—потенциальная кривая возбужденного состояния. Т. к. при электронном переходе по принципу Франка расстояние между ядрами не меняется, то переход ведет в ту точку верхней потенциальной кривой, которая лежит непосредственно над точкой нижней потенциальной кривой, изображающей расстояние ядер в невозбужденном состоянии. Т. о. для нахождения колебательного состояния после возбуждения достаточно провести вертикальные стрелки, как показано на чертеже. При том взаимном расположении верхней и нижней потенциальных кривых, к-рое дано на этом чертеже, переход из «неколеблю-щегося» состояния ведет к образованию сильно колеблющейся возбужденной молекулы (ν=4). Переход же из более высокого колебательного состояния нижней- потенциальной кривой ведет в такую точку верхней потенциальной кривой, которая лежит выше горизонтальной асимптоты кривой, то есть запас потенциальной энергии в этом случае превосходит энергию диссоциации, и молекула испытает распад в результате одного только электронного возбуждения без всякого последующего соударения. Наступление подобной оптич. диссоциации сказывается на виде спектра абсорбции. Именно, пока возбуждение ведет к определенным дискретным уровням верхнего состояния, спектр абсорбции имеет обычную линейчато-полосатую структуру, так как и в нормальном и в возбужденном состояниях мы имеем дискретные уровни энергии. Как только переходы начинают происходить в точках потенциальной кривой, лежащих выше горизонтальной асимптоты, линейчатая структура исчезает, спектр приобретает вид сплошной областрг, совершенно не поддающейся разрешению. Причина состоит в том, что переходы последнего типа завершаются диссоциацией и получающиеся при этом атомы разлетаются с кинетич. энергией, которая имеет сплошной, неквантованный характер. Весьма типичным с этой точки зрения является спектр абсорбции паров J₂, где имеется серия полос, канты которых при переходе к коротким λ постепенно сближаются до полного слияния, за к-рымследует сплошная область абсорбции. Опыт показывает, что, в то время как в дискретной части спектра молекула J₂ при освещении сохраняется как целое, в области сплошного спектра наблюдается диссоциация и притом вплоть до самых низких давлений, когда соударения между молекулами редки.

Не всегда однако сплошной части спектра предшествует дискретная. Нередки случаи, когда последняя вовсе отсутствует и весь спектр абсорбции вещества в газообразном состоянии является сплошным. Таков например спектр абсорбции HJ. Здесь диффузный характер спектра указывает на то, что поглощение всегда завер-. шается диссоциацией, откуда следует, что возбужденное состояние, к которому совершается переход, характеризуется потенциальной кривой, не имеющей минимума, то есть кривой отталкивания (фигура 6). Фотохимия, исследование показывает, что квантовый выход при освещении НJ при всех условиях (от ультраразрежен-

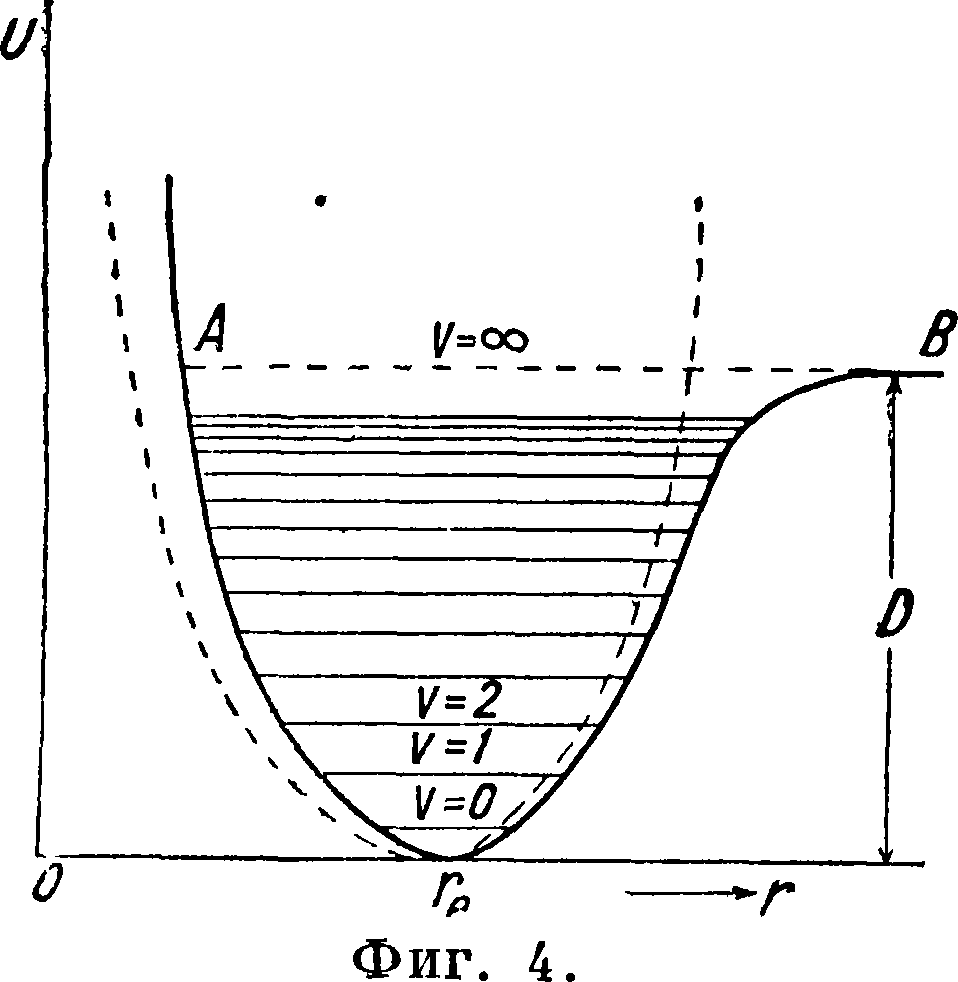
ного состояния до давлений в несколько атмосфер) сохраняет одно и то же значение. Это и указывает на то, что возбуждение молекулы Н J всегда завершается спонтанной диссоциацией, для которой не требуется последующих соударений. Наконец при некоторых условиях спонтанная диссоциация оказывается возможной не только в сплошной, но также и в дискретной части спектра. Это имеет место в случае т. н. предиссоциации (В. Анри, 1925). Спектроскопически это явление обнаруживается в том, что, начиная с некоторой длины волны, внезапно исчезает тонкая структура полос. Полосы как таковые продолжают существовать, но отдельные ротационные линии, из которых они построены, сливаются между собой. Это означает, что, в то время как колебания молекулы еще носят квантованный характер, вращение становится не квантованным. Анри назвал состояние, в к-рое приходят молекулы при освещении длинами волн из области, где наблюдается описанное размывание полос, состоянием пре диссоциации, т. к. молекула в этом состоянии обнаруживает особую химич. активность. В настоящее время установлено, что эта активность обусловлена не «разрыхлением» молекулы, предшествующим диссоциации, как думал Анри, но самой диссоциацией—спонтанным фотохимии. распадом. Причина размывания полос в случае предиссоциации состоит в сильном сокращении времени жизни возбужденной молекулы. Из оптики известно, что идеально тонкую монохроматич. линию может дать только бесконечно длинный ряд волн. Если излучающая молекула пребывает в возбужденном состоянии ограниченный промежуток времени и следовательно дает ряд волн ограниченной длины, то получающаяся спектральная линия должна обладать конечной «естественной шириной», которая тем больше, чем меньше время жизни возбужденной молекулы. Из оценки ширины линий в спектрах предиссоциации можно установить, что т в этом случае порядка 1(П¹³ ск., то есть в 10⁵ раз меньше нормального значения (10^-8 ск.). За этот укороченный период жизни молекула все же может успеть совершить примерно 100 колебаний, но не успеет совершить ни одного оборота (период обращения НПЧ-НГ¹²

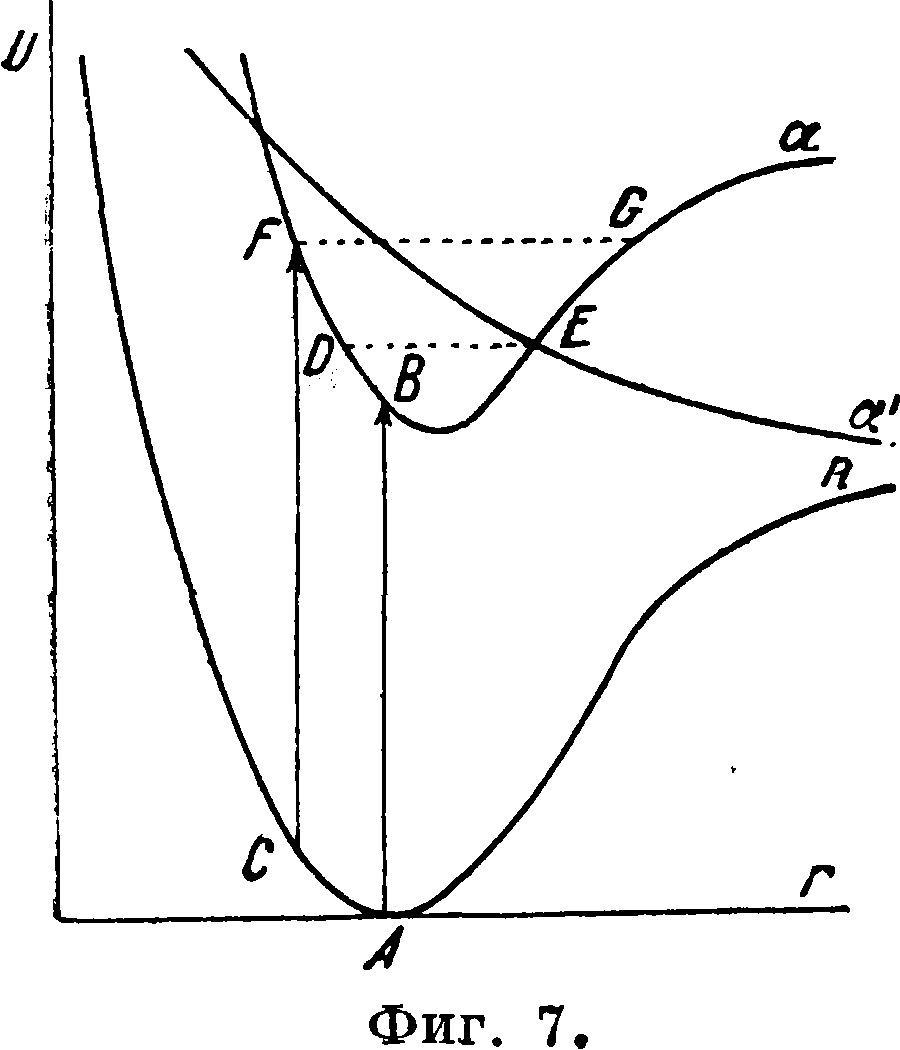
ск.). Отсюда понятно, почему в спектр ах предиссоциации сохраняется квантование колебательных движений и исчезает квантование вращения. Сокращение времени жизни в области предиссоциации обусловлено спонтанным распадом молекулы. Одна из возможных схем такого распада представлена на фигуре 7. Пусть п—обычная потенциальная кривая нормального состояния и пусть те же атомы могут еще взаимодействовать иным способом, а именно так, что потенциальная кривая для этого взаимодействия будет кривой отталкивания а; пусть наконец а — потенциальная кривая возбужденного состояния. Кривые а и а между собою пересекаются; вследствие этого при известных условиях могут осуществляться переходы с кривой а на кривую а—переходы,

влекущие за собой спонтанный распад молекулы. В самом деле, если величина поглощаемого кванта такова, что при возбуждении молекула попадает в какую-нибудь точку В кривой а, лежащую ниже уровня DE, то таким переходам отвечают обычные полосы с тонкой структурой. Если же при возбуждении молекула попадает в область кривой а, лежащую выше уровня ЕЛ, то положение существенно изменяется. Пусть переход ведет в точку F. Попав в эту точку, молекула будет колебаться, как шарик,положенный в чашу с сечением FBG и поднятый на уровень GF. Т. к. этот уровень лежит ниже асимптоты а, то в отсутствии кривой а молекула не могла бы испытать распад. Но кривая а в точке Е пересекает кривую отталкивания а, поэтому, проходя при колебаниях по FDEG через эту точку, молекула будет обладать запасом энергии, равным энергии одного из возможных состояний, отвечающих кривой а. Согласно общему положению квантовой механики между различными состояниями равной энергии, при наличии связи между ними, обязательно должны иметь место спонтанные переходы. Это значит, что если молекула находится в точке Е кривой а, то она имеет конечную вероятность перейти на кривую а.Но последняя есть кривая неустойчивого состояния, и переход на нее завершается распадом, диссоциацией молекулы. Итак, колеблясь по кривой· а, молекула рано или поздно должна перейти на кривую a if в результате испытать распад.

Предиссоциация наблюдается как в сложных молекулах, так и простых. К первым принадлежит например ацетальдегид, в спектре абсорбции которого при А=3 050 А наблюдается исчезновение тонкой структуры полос, одновременно с этим обнаруживается и фотохимич. реакция, при которой ацетальдегид распадается на метан и окись углерода:

СН₃. СОН+hv -> СО+СН4.

В качестве других примеров можно назвать формальдегид, где размывание полос обнаруживается у А=2 800А и одновременно наблюдается реакция

^н

)C—0+hv =Н₂+СО,

В^/

аммиак, сероуглерод и др.

Сопоставляя все сказанное о первичном фотохимич. процессе в газах, мы видим, что единого механизма этого процесса не существует. В одних случаях он сводится к возбуждению молекулы, и тогда для фотохимич. распада требуется еще последующее соударение; в других—первичным процессом служит спонтанная оптическая диссоциация или предиссоциация. Т. к. распад в последнем случае не зависит от соударений, то квантовый выход таких реакций не должен зависеть от давления.

Элементарные процессы в растворах. С практич. точки зрения фотохимич. реакции в растворах являются особенно важными. При истолковании механизма элементарных фотохимич. процессов здесь следует различать два случая: 1) вещества, которые хорошо растворяются в воде, не испытывая электро-литич. диссоциации (галоиды, С0₂, S0₂, Н₂0₂, NH₃ и др.); 2) вещества, испытывающие электро литич. диссоциацию. В первом случае спектр абсорбции в растворе б. или м. приближается к таковому для газообразного состояния.

Поэтому и элементарные фотохимии, процессы в том и другом случае должен быть аналогичными, то есть мы можем ожидать, что у таких веществ первичный процесс будет возбуждением или спонтанной диссоциацией, смотря по тому, в какой части спектра абсорбции возбуждается реакция. Во втором случае спектр абсорбции принадлежит ионам. Здесь часто наблюдаются т. н. спектры электронного сродства, то есть спектры, отвечающие процессу отщепления электрона от аниона и захвату его катионом. Такой спектр наблюдается например у ионов J, Вг, СТ, и в этом случае результатом элементарного процесса будет появление в растворе вместо ионов J и какого-нибудь катиона, например Na“, нейтральных атомов. Действительно при освещении водных растворов иодидов и бромидов можно обнаружить появление свободных атомов J или Вг, а вместе с тем раствор приобретает щелочную реакцию. Описанный переход электрона от аниона к катиону в водном растворе отнюдь нельзя представлять себе как непосредственный перескок электрона. Т. к. растворенный ион окружен огромным количеством молекул растворителя, с к-рыми он находится в состоянии постоянного соударения, то поглощающим центром является не сам ион, но комплекс из иона и слабо связанной с ним молекулы воды, например J, Н₂0. Результатом поглощения кванта таким комплексом является освобождение электрона от J и переход его к связанной с J молекуле Ή ₂0, к-рую этот электрон разбивает на Н и ОН; последующее соударение Н с катионом (например Na*) ведет к перезарядке, в результате которой появляется свободный атом: Na+H=Na+H.

Аналогичную природу имеет спектр абсорбции ионов сульфита SO3, где поглощение света ведет к появлению радикала HS0₃, при посредстве которого осуществляется цепная реакция окисления сульфита кислородом.

Значительный интерес представляют растворы органических веществ, причем здесь также удалось обнаружить нек-рые простые закономерности. Так, оказалось, что все одноосновные кислоты испытывают распад по схеме /R

ОС< +7iv=RH + C0₂.

^хон

Напр. уксусная к-та распадается с образованием 50% СО а и 50% метана:

/СН₃

ОС( +hv -* сн₄+со₂. ^хон

Далее исследование альдегидов и кетонов показало, что все вещества состава 5¹>С=0

реагируют по схеме

Ri₄ R-i

)С-0 + hv-+ 1 +со. r₂^x r₂

Вероятно и самый элементарный процесс протекает по той же схеме, то есть при поглощении света освобождается радикал R_x, к-рый, реагируя с остаточной молекулой R₂CO, дает R_XR₂и СО. Вследствие значительно большей сложности и недостаточной изученности спектров растворов исследование механизма фотохимических процессов в них пока еще в сравнительно немногих случаях привело к установлению такой же отчетливой картины, как это имеет место в газах.

Кинетика фотохимических реакций. Вслед за первичным фотохимии, про цессом обычно следует целый ряд вторичных» которые нередко сильно маскируют механизм явления. Для того чтобы разобраться во всех стадиях процесса, недостаточно одного изучения спектра; необходимо использовать все возможные данные, в особенности величину квантового выхода и кинетику реакции, то есть зависимость ее скорости от различных факторов (интенсивности освещения, концентрации компонентов, температуры и прочие).

Согласно закону Гротгуса-Дрепера-Вант-Гоффа скорость фотохимической реакции для данной длины волны пропорциональна количеству поглощенной энергии. Т. о. если реакция происходит е одном веществе (например распад HJ), то получается кинетич. уравнение вида

dx_ j

dJ—^KJabs>

где ж—концентрация продукта реакции, a J_ahs— поглощенная энергия. По закону Вера-Ламберта

Jabs-Joi 1-е-**),

где J₀—падающая интенсивность, с—концентрация, d—толщина слоя, к—постоянная—коэф. погашения. Если величина kcd достаточно мала, то функцию е~^ш можно разложить в ряд, отбросив все члены со степенями kcd, начиная со второй. В таком случае

af=К Jabs=KJo (1 - <Г^Ш)=K_kcdj₀=К^₀с.

Итак, при малых концентрациях реагирующего вещества скорость реакции должен быть пропорциональна интенсивности падающего света и концентрации реагирующего вещества. Наоборот., если kcd настолько велико, что е~^ш можно без большой погрешности положить равным 0, то т е. скорость реакции пропорциональна падающей интенсивности и вовсе не зависит от концентрации. Оба рассмотренных крайних случая встречаются весьма часто в фотохимич. кинетике. В более общем случае молекула, поглотившая квант энергии и испытавшая вследствие этого возбуждение или диссоциацию, представляет собою лишь начальное звено реакции» за которым следует ряд вторичных процессов. Пусть например реакция между поглощающим веществом состава А₂ и другим участвующим в реакции, но не поглощающим веществом В осложняется тем, что только часть возбужденных молекул А₂“, получающихся вследствие поглощения молекулами А₂ квантов hv, вступает в реакцию с В, тогда как остальная часть возвращается в нормальное состояние, вновь испуская квант hv, то есть пусть процесс проте кает по схеме:

[А₂] + hv [А₂]* fei

[А₂]* -> [А,] + hvfi.h₂

[А₂]* + [В] результ.fe₃

(звездочкой обозначена возбужденная молекула). Полагая, что поглощение слабое, и применяя к отдельным стадиям этого процесса законы химич. кинетики, можно убедиться, что кинетич. ур-ие для конечного продукта реакции имеет уже довольно сложный вид: dx ₌ h₃kiJ₀[A₂l [В]. dt~ fe₂ + ft₃[B] ’

если же начальная стадия процесса состоит в диссоциации молекулы А ₂ по схеме: A₂ + 7w->2A, а исчезновение полученных атомов А происходит в результате воссоединения 2А->А₂, то кинетич. ур-ие осложняется еще тем, что интенсивность J₀ и начальная концентрация А₂войдут в него с дробным показателем степени

(i), то есть скорость реакции будет пропорциональна квадратному корню J₀ и концентрации [А₂1. Подобные случаи в фотохимии, кинетике встречаются довольно часто. В качестве примеров можно указать наразложение озона ультрафиолетовым светом, окисление иода щавелевокислым калием в водном растворе и др. Пропорциональность скорости реакции квадрату интенсивности означала бы, что реакция происходит в результате одновременного поглощения двух световых квантов. Такой случай мало вероятен, и поэтому квадратичная зависимость от интенсивности наблюдается редко.

Влияние t° на скорость фотохимии, реакции, вообще говоря, мало. Темп-рные коэф-ты большинства фотохимии, реакций близки к 1. Тем не менее существует ряд реакций, для которых темп-рный коэф. имеет значительную величину. С точки зрения современной химии, кинетики наличие темп-рной зависимости скорости реакции указывает на существование особой «энергии активации»—избытка энергии, которым должна обладать реагирующая молекула и к-рый в случае темповых реакций черпается за счет термин, энергии. В фотохимических реакциях этот избыток энергии доставляет свет, и этим объясняется отсутствие темп-рной зависимости для большинства фотохимии, реакций. Если однако темп-рный коэф. не равен единице, то это может быть обусловлено двумя причинами: а) темп-рная зависимость скорости реакции м. б. ложной, т. к. на самом деле под влиянием t° изменяется спектр абсорбции чувствительной компоненты, б) в случае «истинного» влияния t° это последнее указывает на значительную величину энергии активации тех темповых процессов, которые следуют за первичной чисто фотохимия. реакцией. Так например, значительный температурный коэф. реакции Вг₂ + Н₂ 2НВг находит себе объяснение в том, что вслед за первичным процессом Br₂ + hv-+ 2Вг следует вторичный Вг + H₂-*HBr + Н, требующий значительной энергии активации в 16,2 Cal.

Истолкование фотохимия, реакций. К числу простейших фотохимия, реакций принадлежит фотохимия, разложение HJ и НВг, происходящее в ультрафиолетовой части спектра (в интервале 2 820 -f- 2 070А). В том и другом случае квантовый выход для всех длин волн равен 2 и совершенно не зависит от давления. Спектры абсорбции обоих веществ в газообразном состоянии сплошные—без дискретной части. Последнее обстоятельство прямо указывает на то, что первичный процесс есть спонтанная оптич. диссоциация. Следовательно для HJ имеем: HJ + hv=Н + J. Образующиеся атомы Н и J могут затем реагировать разными способами, а именно:

I.	H+HJ=H2 + J	+ 32,1 Cal
II.	H+J2=Н J+J	+ 33,7 Cal
III.	J + H2=JH + H	- 32,1 Cal
IV.	J+HJ=J2 + II	- 33,7 Cal
V.	H + H=H2	+ 101,9 Cal
VI.	J+J=J,	+ 35,3 Cal
VII.	J + H=HJ	+ 69,8 Cal

Из этих реакций для атома Н практически может осуществиться только I, т. к. концентрации компонентов, необходимых для реакций II, V и VII, слишком ничтожны; для атомов же J осуществима только реакция VI, т. к. реакции III и IV требуют значительных энергий ак тиваций и потому протекают крайне медленно„ •реакция же VII отпадает из-за незначительности концентрации Н-атомов, исчезающих при реакции I. Так. обр.полная схема реакции будет:

HJ+hv=H + J H + HJ=H₂ + J j+j - j₂2H=H₂ + J₂

T. e., в согласии с экспериментом, на один поглощенный квант разлагаются две молекулы HJ* Значительно сложнее протекает реакция образования НВг из Н₂ + Вг₂. Чисто кинетич. исследование привело к следующей зависимости от концентраций компонентов для случая, когда, реакция протекает термически без освещения: -i[НВг] fe[H₂]/[Br₂] dt, 2[НВг]

^т+1в

Фотохимия, образование НВг подчиняется аналогичному ур-ию с тем добавлением, что скорость реакции пропорциональна квадратному корню из числа поглощенных световых квантов. Это сложное ур-ие м. б. полностью истолковано, если принять во внимание вторичные реакции, следующие за первичным процессом:

Вг₂ + hv=Br+Br Вг + Н₂=НВг+Н -13,2 Н + Вг₂=НВг + Вг+40,5 Н + НВг=Н₂ + Вг+16,2 Вг + Вг=Вг₂ + 45,2

Разница в кинетике последнего процесса и разложения HJобъясняется иными термохимия, соотношениями: так например,реакция J + НJ=J₂-f II требует затраты 33,7 Cal, а реакция Вг+НВг= =Вг₂+Н протекает с выделением 16,2 Cal.

Наиболее сложной и вместе с тем наиболее интересной является реакция Бунзена-Роско: фотохимическое образование НС1 из Н₂ и С)₂. Одна из наиболее поразительных особенностей этой реакции состоит в том, что квантовый выход ее достигает огромной величины: на один поглощенный квант приходится до 10⁵ образовавшихся молекул НС1. Объяснение этой особенности дано впервые Боденштейном, к-рый указал на то, что реакция Н₂ + С1₂ является типичной цепной реакцией (смотрите): каждый элементарный фотохимия, процесс является лишь начальным звеном целого ряда реакций, к-рые· непосредственно следуют друг за другом, создавая цепь реакций, распространяющуюся в пространстве до тех пор, пока она не встретит стенку сосуда, на которой цепь обрывается. Обрыв цепи может произойти также и в объёме газа при встрече цепи с молекулами некоторых веществ^ обладающих способностью сильно тормозить реакцию. Наиболее близкая к действительности формулировка отдельных процессов, составляющих звенья цепи, дана Нернстом:

I. Cl₂ + 7iv=2С1

II. С1+Н₂=НС1 + Н -0,5 Cal

III. Н+С1₂=НС1 + С1 +41,5 Cal и т. д.

Здесь только реакция II требует небольшой теплоты активации, зато реакция III протекает с большим выделением тепла. Именно поэтому отдельные реакции, образующие звенья цепи, протекают легко при каждом соударении, вследствие чего, раз начавшись, цепь уже сама идет до вынужденного обрыва. Значительное выделение теплоты, сопровождающее цепь, позволило Вейгерту и Келерману сделать распространение цепи видимым. С этой целью они использовали изменение показателя преломления вследствие нагревания и применили для обнаружения цепи т. н. «метод полос» Теплера, пря помощи которого можно было наблюдать разви тие цепи на темном фоне в виде светлой полосы, постепенно заполняющей реакционное пространство. Цепные фотохимич. реакции наблюдаются не только в газах, но также и в растворах. Сюда относятся например реакции между иодом и щавелевокислым калием в растворе, т. н. реакция Эдера (реакция между сулемой и щавелевокислым аммонием в растворе), окисление сульфита SOg в сульфат SO". Цепной характер последней реакции был впервые обнаружен Бекштремом, к-рый показал, что реакция сохраняет свой цепной характер и тогда, когда она возбуждается термич. путем без участия света. Это открытие дало повод к перенесению цепной теории от фотохимич. процессов к обычным темповым реакциям, причем Семеновым была развита стройная теория цепных реакций, с особенным успехом примененная им к истолкованию ных процессов.

Применение фотохимич. процессов в технике. До настоящего времени только одна группа фотохимич. реакций получила широкое технич. использование—фотохимическое разложение галоидо-серебряных солей. Кроме этого большое практич. значение имеют также различные биологич. процессы, вызываемые светом (стерилизация воды ультрафиолетовыми лучами, фототерапия и др.). Т. к. фотохимич. процессы в настоящее время впервые получили наиболее полное теоретич. истолкование, то можно ожидать в недалеком •будущем значительного развития также и прикладной Ф. Можно думать, что наиболее прямой путь к технич. методам использования солнечной энергии ведет через Ф. В разрешении этой проблемы особую роль играет детальное исследование процесса ассимиляции углерода зеленым листом растения, изучение которого яри помощи точных физич. методов еще только начато. Основную роль в этом процессе играет передача энергии от молекулы хлорофилла, поглощающего углерод в видимой части спектра, к исходным веществам фотосинтеза—углекислоте и воде, имеющим полосы абсорбции в далекой ультрафиолетовой части; фотосинтез— типичная фотосенсибилизированная реакция. Работы О. Варбурга (сына) и Э. Негелейна показали, что в этой реакции выполняется фотохимич. закон эквивалентности, на основании которого выход уменьшается с уменьшением длины волны. Определение энергетич. выхода реакции показало, что у исследованного Варбургом и Негелейном объекта (зеленая водоросль Chore] 1а) использование поглощенной энергии достигает 70%, в то время как наибольший из известных выходов для других фотохимич. реакций составляет 50% (реакция 30₂-*20₃). Самый механизм фотосинтеза еще неясен, а попытки воспроизвести его in vitro при помощи различных сенсибилизаторов оказались неудачными.

Лит.: К ё п А. и Юнг Г., Фотохимия, пер. с нем., М.—Л., 1933,-Теренин П., Введение в спектроскопию, Μ.—Л., 1933; Кондратьев, Фотохимия, М.—Л.,

1933; Лазарев П., Основы учения о химич. действиях света, II., 1919—1920; Шпольский Э., «УФН», 1927, т. 7, стр. 433, 1933, т. 13, стр. 325;

«УФН», 1933,т.13, стр. 325; Семенов Н., «Успехи химии», 1932, т. 1, стр. 19; Гиншельвуд Ч., Кинетика газовых реакций, пер. с англ., М.—Л., 1933; Kistiakowsky G-., Photochemical Processes, Ν. Y., 1928; Berthoud A., Photochimie, P., 1928; Grif-f i t h R. a. Me К e о w n A., Photoprocesses in Gaseous a. Liquid Svstems, L., 1929; Style D., Photochemistry, L., 1930; ‘B onhoeffer K. u. Harteck P., Grundlagen d. Photochemie, Dresden—Leipzig, 1933; Kassel L., The Kinetics of Homogeneous Gas Reactions, N. Y., 1932; Spoehr H., Photosynthesis, New York, 1926. Э. Шпольский.