Функция

Функция в математике, переменная величина, значение которой определяется значением другой (или нескольких) переменной величины. Если возможно произвольно выбирать величину числа х, принадлежащего совокупности чисел в интервале между а и b а<х<Ь,

то х называют непрерывной переменной величиной в данном интервале. Если при этом каждому значению х соответствует по некоторому закону определенное значение у, то у является Ф. х, что символически может быть выражено:

y=f(p), У=<Р (®), y=F(x) ит. п.

В указанном обозначении буквы f, <р, F,. называются характеристикой Ф.;характеристика обозначает комплекс действий, которые надо произвести над величиной х, чтобы получить величину у. Здесь х носит название независимой переменной или аргумента Ф. В рассмотренном случае к интервалу были причислены его концы; если этого нет, то величина х ограничивается условием а < х < b.

В первом случае интервал называют замкну-т ы м, во втором—д вусторонне открыты м. В случаях а<Ж Ь или а<ж< b интервалы называют по л у-или односторонне открытыми. Если непрерывная перемен

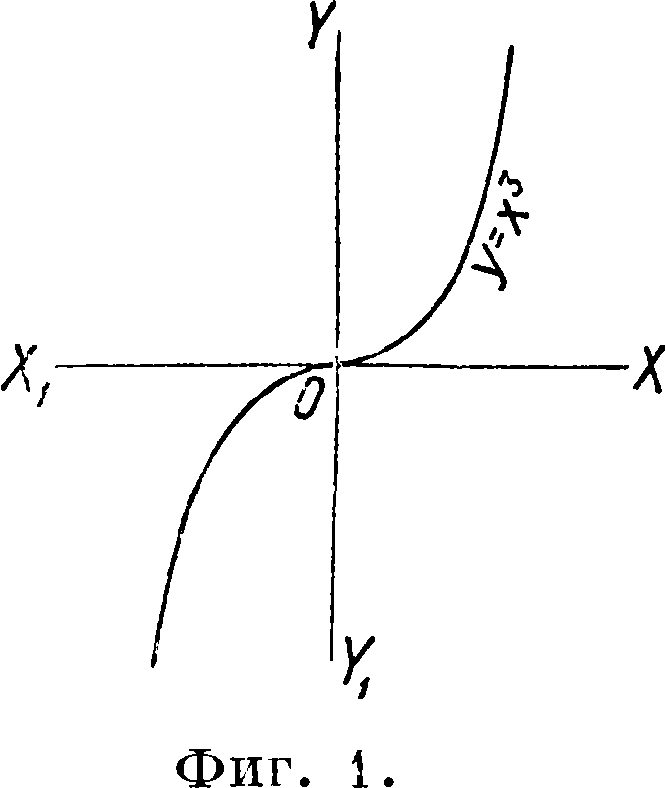
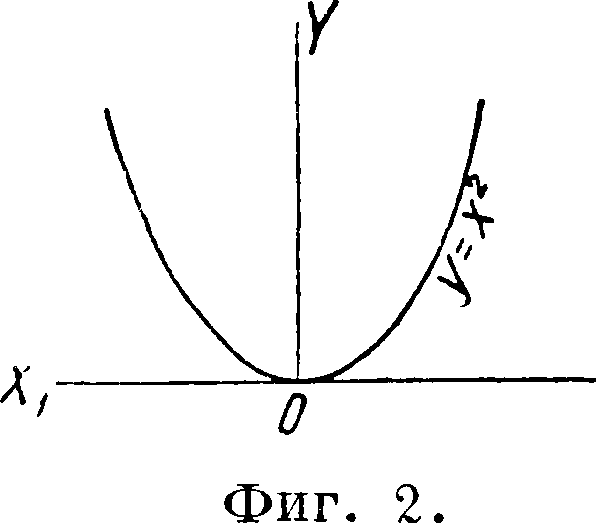
ная пробегает бесконечный интервал, то или a<i ж<Соо, или — оо < b, или — оо<ж<оо.

Пользуясь прямоугольной системой координат, функциональную зависимость величины у от величины х можно изобразить графически; геометрии, образом Ф. будет служить вообще кривая. Обыкновенно соответствие Ф. у аргументу а? устанавливается однозначным образом, например у ^=х^г или у=cosх; здесь каждому значению х соответствует только одно значение у; у называют однозначно и Ф. от х. Если же каждому значению аргумента соответствует не одно, а несколько значений у, то у называют многозначной Ф. от ж, например ур-ие у²= х определяет у как двузначную Ф. от х, т. к. у=±]/ж. Аналогично из равенства у=arc tg х у определяется как многозначная Ф. от ж, т. к. при всяком данном значении х число значений у бесконечно велико, например если ж=0, то у=пл,

где п—любое целое число. Для устранения многозначности Ф. вносят добавочное условие, например у>0 или 2/< 0, что выделяет однозначную ветвь многозначной Ф. Если Ф. однозначно определена на всем своем протяжении, то изображающая ее кривая пересекается всякой прямой, параллельной оси OY, только в одной точке. В случае многозначной Ф. указанные параллели имеют несколько точек пересечения с кривой. На фигуре 1 изображением Ф. y~x^z является кубическая парабола.

При исследовании Ф. наиболее важную роль играет ее непрерывность. Это свойство Ф. выражается в том, что при весьма малом изменении х значение у также изменяется весьма мало (не делает внезапных скачков), то есть кривая на всем своем протяжении не разрывается. Ф., имеющая для всех значений х в нек-ром интер

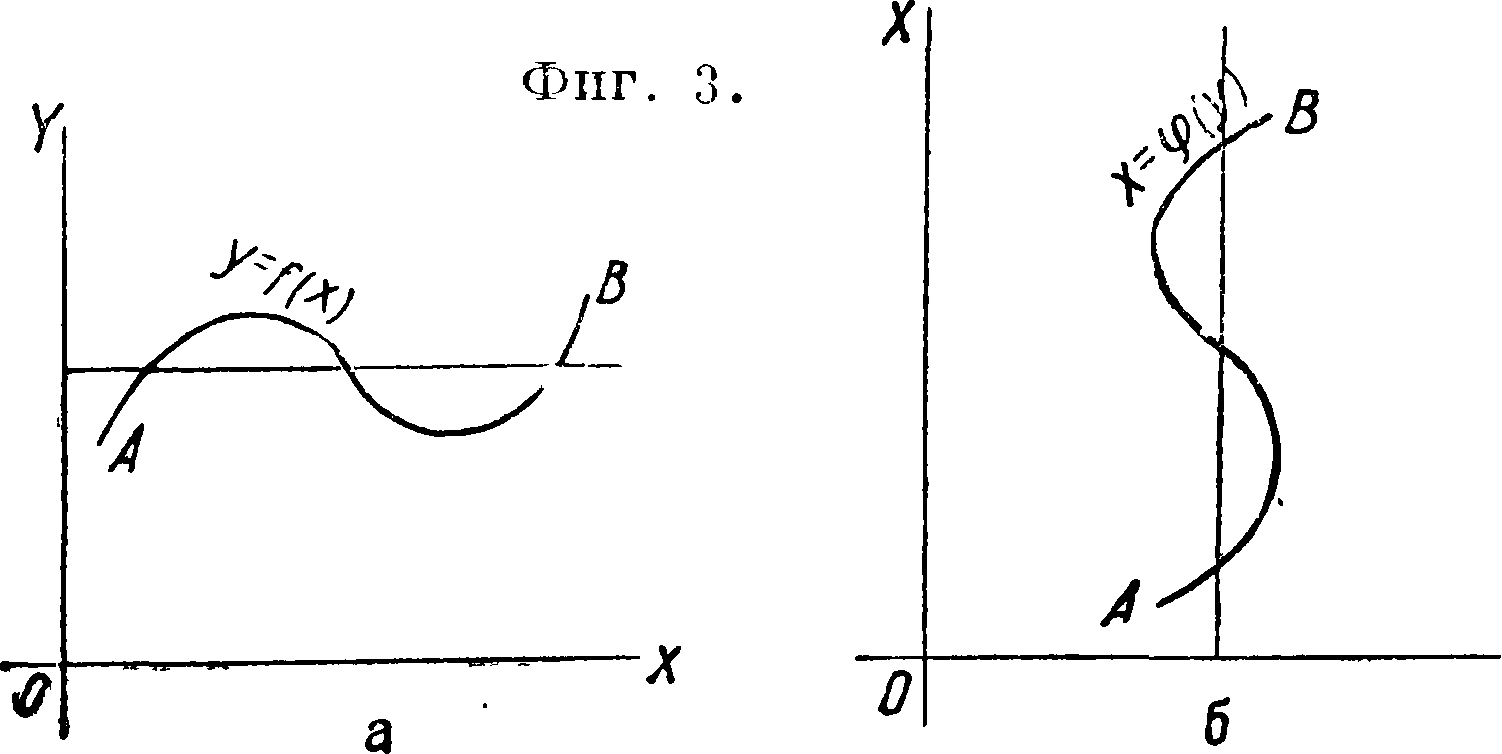
вале одно и то же значение, называется константою, или постоянной; ее изображением служит прямая, параллельная оси ОХ. Если в избранном интервале большему значению х всегда соответствует большее значение у, то Ф. называют монотонно возраста ю-щ е й, если же большему значению х всегда соответствует меньшее значение у, то Ф. называют монотонно убывающей в этом интервале. Если кривая y=f(x) симметрична относительно оси OY, то есть если одно и то же значение Ф. соответствует как значению х=— а, так и значению х=а, иначе—если f (— х)=f(x), то Ф. называют четной, например у =х² (фигура 2). Если же кривая симметрична относительно начала координат, то есть если f (— х)=— f (ж), то Ф. называют нечетной (фигура 1).

Обратные Ф. Формальную зависимость между двумя величинами можно рассматривать двояко: или первую величину принимать за Ф. второй или наоборот; например функциональная зависимость у=х² м. б. выражена ур-ием х=У у, причем х=φ (у) по отношению к y=f(x) называют обратной Ф. Графич. изображение обратной Ф. может быть получено поворотом системы координат вместе с кривой у=f(x) около

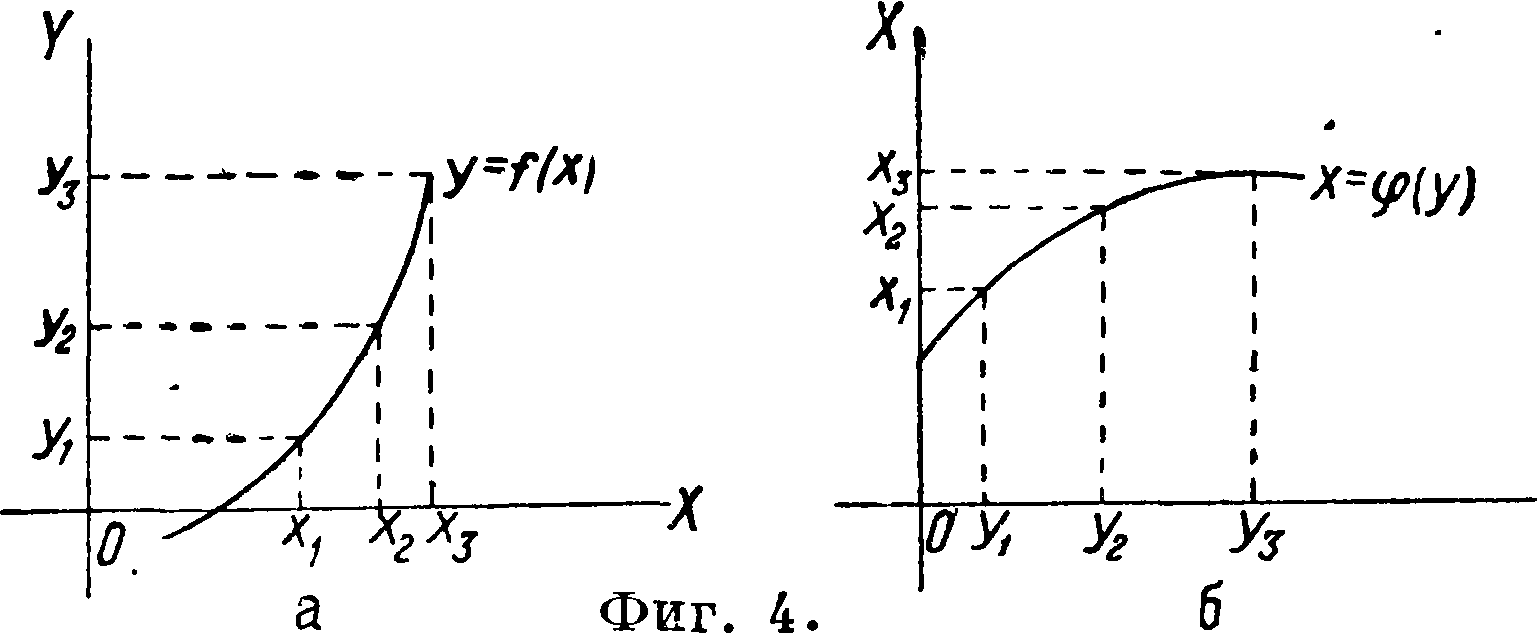
биссектрисы угла XOY на полоборота (фигура 3, а и б). Из чертежа ясно, что Ф. y=^f(x) не будет однозначно обратимой, т. к. кривая, соответствующая ей, пересекается прямою у=с в нескольких точках. Если же Ф. y=f(x) в рассматриваемом интервале непрерывна и монотонна, то она обратима при помощи однозначно определенной непрерывной Ф. (фигура 4, а и б).

Из предыдущего видно, что Ф. можно рассматривать как первично заданную, но можно исходить и от геометрически заданной .кривой. Кроме того существует табличный способ задания Ф., например для y=sin ж, где не указаны арифметич. действия, посредством которых можно было бы по данному значению х вычислить соответствующее значение у. При табличном задании значения Ф. приведены только че

рез определенные интервалы; для вычисления значений Ф., соответствующих промежуточным значениям х или выходящих за пределы таблицы, применяются приемы, носящие название интерполирования (смотрите Вычисления приближенные) или экстраполирования (смотрите).

Классификация Ф. — см. Исчисление бесконечно малых.

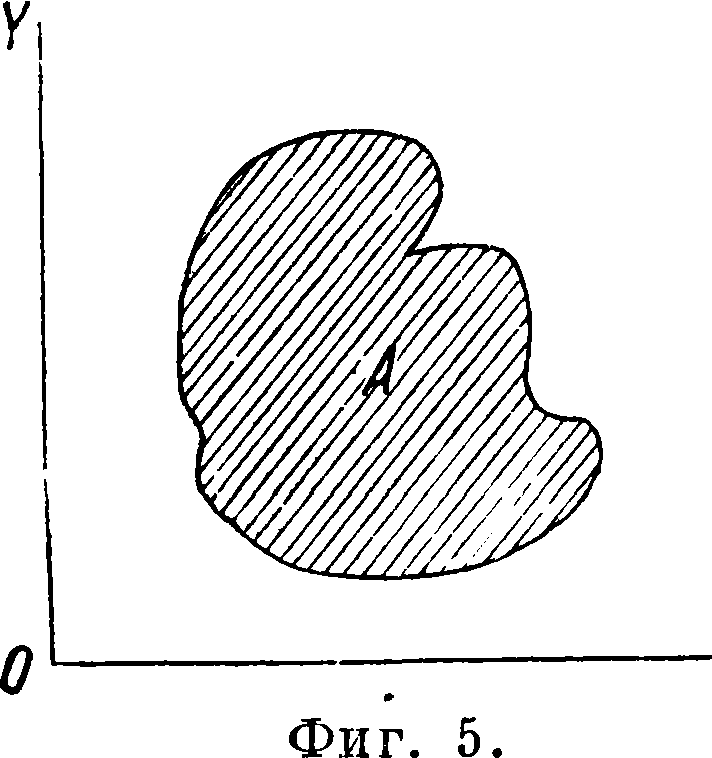
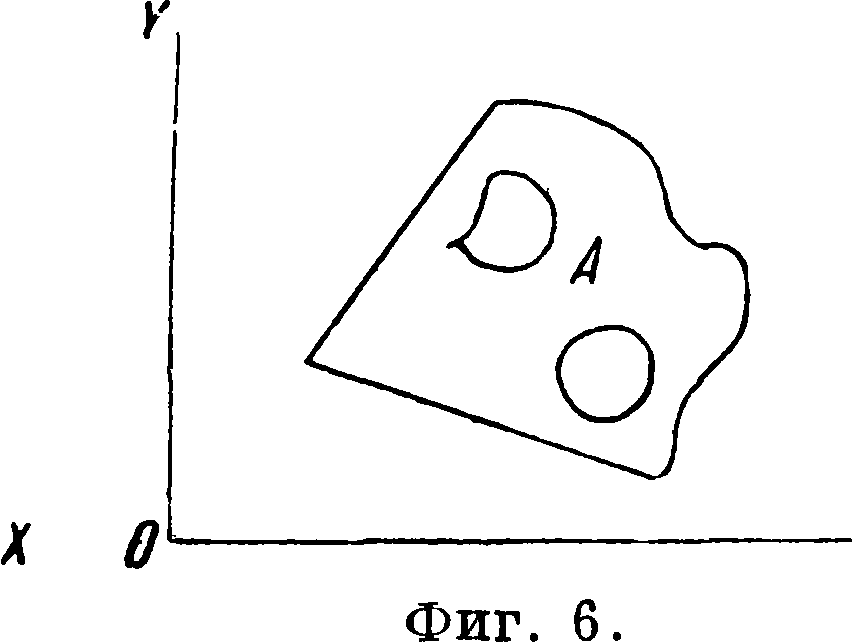
Ф. от многих переменных. Если каждой паре значений х и у соответствует по какому-нибудь закону значение и, то и называют Ф. от независимых переменных х и у. То же относится и к большему числу независимых переменных. При непрерывно изменяющейся паре аргументов точка (ж, у) может быть выбрана где угодно внутри определенной о б л а с-т и А плоскости XOY (аналогично интервалу для одной независимой переменной). Область А может состоять из части плоскости, ограниченной единственной замкнутой кривой (односвязная область, фигура 5); область А м. б. ограничена несколькими замкнутыми кривыми (многосвязная область). Число ограничивающих кривых определяет «число связности». На фигуре 6 дана трехсвязная область. Геометрически Ф. от двух переменных можно представить с помощью поверхностей, рассматривая пространственную систему координат ж, у и и. Другое геометрии, изображение хо-,_х да Ф. достигается с помощью линий уровня (линий равных высот, линий равных глубин ит.д.). На фигуре 7 приведены линии уровня функции и= х² + у². См. также Эллиптические функции, Шаровые функции.

Лит.: Курант Р., Курс диференциального и интегрального исчисления, ч. 1 и 2, пер. с нем., 2 изд., М.—Л., 1931; см. также Дифференциальное исчисление и Интегральное исчисление. В. Никаноров.