Фурье теорема

Фурье теорема. Франц, математик Жан Баптист Жозеф Фурье (1768—1830 гг.) впервые сформулировал свою знаменитую теорему в начале прошлого столетия следующим образом: всякая периодич. функция м. б. представ те-на в виде конечного или бесконечного ряда

f (£)=+ а_г cos t + а₂ cos 2t -f- а_г cos St +. +

+ b₁ sin t + b₂ sin 2t + b₃ sin St +. (1)

Коэфициенты этого ряда имеют вид

2л а_п=i I* f (0 cos nt · dt, о

2л

f(t) sin nt-dt. о

Первый член ряда представлен в виде потому что при подстановке в выражение для а_пп — 0 мы получим этот коэф. в виде

Покажем, что если данная ф-ия м. б. представлена в виде указанного ряда, коэф-ты а_п и Ь_п должны иметь вышеуказанный вид. Т. к. обе стороны ур-ия (1) идентичны для всех значений t, то они должны оставаться идентичными и после совершения над ними одинаковых операций. Умножим обе части этого ур-ия на dt и проинтегрируем их в пределах от t — 0 до t — 2 π.

2 л 2л

cos nt - dt=0 и J sin nt}· dt=0,

υ и то мы имеем:

^τ·κ· Г

[2 л υ

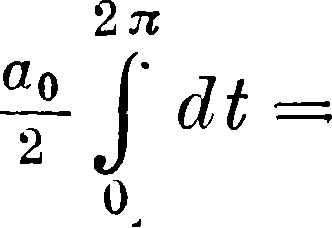
πα₀.

Лит.: Ушаков С., Искусственные смолы, Л., 1929 (смолы из Ф., перечень патентов); Д еснер Г., «Маслобойно-жировое дело», М., 1929, 9 (50), стр. 32; его же, там же, 1931, 2—3, стр. 36; Райгородский М., там же, 1931, 8—9, стр. 62; Четвериков Н., там же, 1932, 3, стр. 50; Челинцев В. и Воробьева А., «ЖХП», М., 1933, 2, стр. 27; Д еснер. Г., «ЖХП», 1930, т. 7, стр. 695 (физич. свойства Ф.); М и р-л и с Д., там же, 1931, т. 8, стр. 697; Гофман М.и Корневич К., «Химия твердого топлива», М., 1930, 5, стр. 51 (применение Ф. для очистки антрацена); Оборин В., «Журнал прикладной химии», М., 1930, т. 3, стр. 231; П о р а й-К о ш и ц А. и Иттенберг Ш., там же, 1932, т. 5, стр. 761 (применение Ф. в текст деле); Порай-Кошиц А., Кудрявцев Н. и Машки-л е и з о н Б., там же, 1933, т. 6, стр. 685 (механизм конденсации Ф. с фенолом); Орлов Н. и Рыклис С там же, 1933, т. 6, стр. 910; Дерибас Д. и Шиллер Г., «Вестник кожевенной промышленности», М., 1931, 7, стр. 34 7; Д e р и б а с Д. и Шиллер Г., Кожевенно-обувная промсть СССР, М., 1932, 10, стр. 601 (дубильные вещества из Ф.); «Бюллетень пластмасстроя», М., 1931 (материалы конференции по Ф. при НИС ПТЭУ ВСНХ); Пора й-К о ш и ц А., Сов. П. 1868/1924 (получение Ф. из лузги); Поварни н, Сов. П. 16199/1927 (получение Ф. из надсмольной воды); Ан. П. 340102/1930; «I. Eng. Chem.»: 1918, у. 10, р. 925; 1921, у. 13, р. 133, 499,823, 1024; 1923, у. 15, р. 65, 499, 823, 970, 1057, 1167, 1255; 1924, V. 16, р. 130, 356; 1926, У. 18, р. 812, 1217; 1927, у. 19, р. 422; Miner С., T г i с k 1 е у J. а. Brownlee Н., «Chemical a. Metallurgical Engineering», Ν. Y., 1922, у. 27, p. 299 а. 362 (приведена лит. по 1921 г.); «Chemical Trade Journal», L., 1926, у. 78, p. 407, v. 79, p. 761; F a i r b г о t h e r H., «Industrial Chemist a.

Это и есть значение интеграла, получаемое при подстановке п=0 в ур-ия (2). Умножим теперь обе стороны ур-ия (1) на cos nt · dt и проинтегрируем его в пределах от 0 до 2 л.

2л

Т. к. J cos mt · cos nt · dt — 0, если m неравно η

о или равно π, кроме этого

2л

J¹ sin mt · cos nt · dt — 0,

* о то, если m=n, мы имеем:

2 л 2 л

J f (t) cos nt · dt=a_mJ cos² nt · dt — л a_n.

υ о

Таким же образом, умножив обе стороны ур-ия (1) на sin nt · dt, проинтегрировав их в пределах от 0 до 2 π и принимая во внимание, что

2 л

J sin mt · sin nt · dt=0_#

если т не равно п или равно π, то, если т=п. мы имеем:

2 я

J* f(t) sin nt · dt=b_n J·sin

² nt · dt=nb_n

Коэф-ты α₀, a_n и определятся отсюда в согласии с выражениями (2).

Слагаемые ряда (1) называются гармониками, а также косинусоидами первого порядка, Ь_п sinnt—синусоидой тг-го порядка и т. д. Как косинусоида, так и синусоида тг-го порядка проходит через п циклов изменений в течение одного периода ф-ии f (t). Каждую пару таких гармоник тг-го порядка можно сложить вместе. Полученная сумма имеет вид а_п cos nt + Ь_п sin nt=Yа% + b · sin (nt + φ_η),

где

4Ψη=ψ_η·

Коэф-ты а и Ь называются амплитудами соответствующих гармоник. Сложив каждую из пар гармоник (косинусоиды и синусоиды), мы получим ряд Фурье в другом виде:

со

f №=у- + 2 ^А»^sin (^nt + Vn

где

A_n=Yal + b

Ф.т. находит себе обширное применение при всевозможных исследованиях колебательных движений упругих тел, вызываемых в последних действием периодически изменяющихся сил. При исследованиях вибраций поршневых двигателей, колебаний мостов, колебаний фундаментов машин, при исследовании тепловых процессов и т. д. Ф. т. является чрезвычайно важным средством,позволяющим глубоко вникнуть в природу перечисленных явлений. При употреблении Ф. т. однако допускается весьма серьезная ошибка, сущность которой заключается в утверждении, что упругие колебательные движения какого-либо порядка могут быть вызваны только гармоническими силами того же порядка. В действительности колебательные движения р-го порядка м. б. вызваны гармонии. силами порядка р, 3 р, 5 р, ., ftp, где ft— любое целое нечетное число (смотрите Гармонический анализ, Колебательные движения, Скорость критическая). Для доказательства этого рассмотрим ряд Фурье вида оо

У=2 (^ап sin па + Ь _п cos па).

71=0

Представим себе кривую, представляющую эту ф-ию вычерченною в прямоугольных координатах, по оси t которых откладываются значения а и по оси у величина у. Разделив отрезок Т, представляющий период данной ф-ии,

на 2 р равных интервала проинтегрируем ф-ию у по этим интервалам, меняя каждый раз знак. Получим сумму т

2р

3 Т

2р

ydl-j ydt + J у dt —. — J ydt.

(2p-l )T

2 T

Представим себе вместо величины t равнознач-т ную ей величину ^а, получим эту сумму в виде

S=-

р р 2 л

J у da - J у da +. - J у da

О я (2 р —1) π

р Р

Сумма S должен быть независима от Ь_п и должна зависеть только от тех а_п, у которых значение п есть нечетное кратное целого числа р. Иными словами, сумма S должна обратиться в нуль при подстановке частного значения у—Ь_п cos пх для значений п—четных и нечетных кратных р, а также при подстановке 2=a_wsinm* для значений п—четных кратных р. При значениях п=ftp—нечетных кратных р подстановка y=a_nsinna должна дать сумму S, отличную от нуля. При подстановке у—Ь_п cos па мы получаем

Si=Lb_n

2 я

J* cos па · da — j* cos па · da -j-. —

2л

— J cos na · da

(2 p-1) я P

T n 1 i.

= — o_n - < SI 2π ⁿ η l

лп

sm--

(. 2лп. лп. (. Зяп 2лп

V p p ¹ p P

Г · Ο · (2ρ-ί)πη"Π τ Γ2 · ^πη

- [sin 2 πη - sm i—^-J }=^ К |_- (sm - -

2 лп,. 2р —1 1. ₀ "1

— sin-- -. -psin——πη]—sin2^ ·

Каждое из слагаемых этой суммы равно нулю при значениях п как четных, так и нечетных кратных p. Т. о. при этом S_± =0, что и требуется нашими условиями. Подставим теперь у=а_п sin па:

~~ 2 л ^αγι

2 л т

J sin па · da — j sin па · da -j-. —

2 л

— J sin na · da

{2р-1)л

(_Л лп

COS--

= ~ a_n - {(cos 0 - cos -

2л ⁿ n P )

COS-

. 2 лп P

)+(

3 лп 2лп

COS— COS

7l7l _

P "*

(2 p —1) лп P

— cos 2 j

T lp лп, л 2 лп л 3 лп i

= — a_n 1 — 2 cos--h 2 cos--2cos--h .·· —

2л ⁿ n _ p ¹ p P

-2cos^i^_+l]==T_a4[l__{coif +}

. 2 лп

+ COS —-. — COS

(2p-l) лп P

]·

Нетрудно видеть, что при четных значениях ft=^ сумма

*и при нечетных значениях к=~ эта сумма отлична от нуля и равна

⁼ * ^ап * п^ ¹ + ¹ + ··· + *)⁼

„_т 4р _2Т о“

""2я η я к *

Это выражение представляет собой площадь, ограниченную синусоидой порядка р с периодом Тис амплитудой ^ а_и=-γ. Эта площадь представляет собой импульс одного периода колебательного движения порядка р, вызванного гармоническими силами порядка п=кр, где к — любое нечетное число.

Лит.: Привалов И., Ряды Фурье, 2 изд., М.—Л., 1931; Мартенс Л., Динамика поршневых двигателей, М., 1932; см. также Гармонический анализ, Скорость критическая, Колебательные движения. Л. Мартенс.