> Техника, страница 90 > Ходкость судна

Ходкость судна

Ходкость судна, способность его под действием движителя (смотрите Движители судовые) развивать данную скорость хода. Для этого движитель должен развивать толкающее судно усилие, по величине равное и обратно направленное горизонтальной продольной составляющей воздействия воды и воздуха на судно при данной скорости, называемой сопротивлением судна. Т. о. сопротивление разделяется на сопротивление воздуха и имеющее у нормальных судов превалирующее значение сопротивление воды; первое определяется по обычным способам аэродинамики (смотрите), последнее входит в теорию корабля и составляет наиболее трудный и не поддающийся в надлежащей мере математическому анализу отдел ее. Гидродинамика несмотря на сильное развитие этой науки не может в полной мере разрешить выдвигаемые практикой вопросы, помогая лишь до некоторой степени их надлежащей ус-тан эвке и освещению. Поэтому в основном во-прзсы X. базируются на экспериментальных данных, в особенности на работах англ, исследователя В. Фруда. До Фруда были разрозненные попытки освещения этого вопроса, не давшие какого-либо определенного метода установления мощности механизмов для достижения заранее определенной скорости движения судна. Позже Фруда ряд исследователей уточнил нек-рые спорные вопросы, но в основном метод Фруда остался до настоящего времени непоколебленным. Полное сопротивление И_п, оказываемое водою передвижению судна, Фруд разделил на три части: волновое R₆< водоворотное R_6V и сопротивление трения R_m, то есть

R_n=R_e -J- R_6P -J- Rm·

Вследствие разности давлений в оконечностях судна и в средней его части при движении судна на поверхности воды возникают волны. Эти волны из-за взаимного трения частиц воды будут постепенно исчезать, а на их место“ в волновое движение будут увлекаться новые массы воды. Образование волн требует постоянной затраты энергии, восполняемой работой движителя и выражаемой при данной скорости некоторой силой, называемой волновым сопротивлением. Чем больше скорость, движения, тем большую часть от полного сопротивления составляет волновое сопротивление. Трение воды о подводную поверхность судна вызывает в вей частью поступательное движение, частью же вращательное. Последнее выявляется в виде мелких вихрей или водоворотов, возрастающих с увеличением скорости. Вместе с тем приходят в движение и далее?· отстоящие от корпуса судна струи воды, вследствие чего вокруг движущегося судна образуется как бы водяная оболочка, участвующая в общем его движении, но со значительно меньшей скоростью. Вследствие разности скоростей? объём воды, увлеченной трением о подводную· поверхность судна, отстает от него, за кормой образуется поток, следующий за судном и называемый попутным следом, или попутным потоком. Наряду с мелкими водоворотными движениями существуют водовороты, вызываемые формой движущегося судна. Причиной их является резкое изменение направления подводной поверхности судна, нару-шающзе при известных скоростях правильное-обтекание водою судна. Нарушения формы обводов судна выражаются как в виде резкого обрыва поверхности (срез кормы), так и в очертаниях ватерлиний (выпуклости, впадины). Всякие выступающие части (кронштейны гребных валов, рули, ахтерштевни и тому подобное.) также являются причинами водоворотов. У морских судов с плавными обводами водоворотное сопротивление невелико и обычно не превышает

5—8% полного сопротивления. Отдельно водоворотное сопротивление не вычисляется и опытным путем не определяется, а всегда рассматривается совместно с волновым сопротивлением. Оба вида этих сопротивлений образуют вместе т. н. остаточное сопротивление R₀=R_e- -R_6P. Т. к. вода обладает вязкостью и сцеплением, то при движении судна она оказывает на подводную· поверхность касательное усилие. Последнее при прочих равных условиях будет тем больше, чем большей шероховатостью обладает подводная поверхность. Это касательное усилие, отнесенное ко всему судну, называется сопротивлением трения. При нормальных средних скоростях сопротивление трения играет доминирующую роль (при небольших скоростях 80— 90% полного сопротивления).

Сопротивление трения. Изучение трения тел, движущихся в жидкостях, начинается с опытных исследований Кулона и Боффуа. Основание современного знания трения воды было положено В. Фрудом. Исследования сопротивления трения Фруд делил на три отдела: 1) на определение закона изменения сопротивления в зависимости от скорости;

2) на определение различия в сопротивлении в завизимостй от состояния поверхности; 3) на •определение различия в сопротивлении на единицу поверхности, зависящего от различия длин поверхности. Для устранения по возмож—

ности иных видов сопротивления (кроме трения) Фруд для опытов брал тонкие широкие доски разной длины (2—50 фт.) с заостренными концами и буксировал их под поверхностью· воды в бассейне с различными скоростями. Поверхность досок покрывалась различными веществами, как то: лаком, парафином, коленкором, оловом и песком. Из опытов Фруд вывел, что сопротивление трения выражается ф-лой г=fsvⁿy

где г—сопротивление трения доски в англ, фн.,

&—полная поверхность доски в фт.², v—скорость в фт./ск., и п—постоянные для данной доски, зависящие от длины и состояния поверхности. Коэф. трения f не зависит от давления и глубины погружения доски, изменяется пропорционально увеличению шероховатости поверхности и уменьшается с увеличением длины доски, причем для досок свыше 50 фт. длиною можно считать его при данном состоянии шероховатости постоянным. Показатель п для коротких досок равен 2, а для длинных несколько меньше. Фруд также установил, что плавные очертания подводной поверхности судна, покрытые ровным слоем краски, будут иметь то же сопротивление трения, что и парафиновые поверхности для моделей. Полученные результаты Фруд экстраполировал и для судов, имеющих длины, значительно превышающие длины досок, примененных для опытов, т. ч. ^сопротивление трения для судна выразил той :же ф-лой (лишь все числовые значения должен быть отнесены к судну). Для перехода же к действительным судам необходимо было бы: а) довести испытания до длин в 300ж, б)довести испытания ;до скоростей, превышающих более чем в 4 раза иаивысшие скорости, применявшиеся при опытах, в) сделать переход от плоских поверхностей к кривым для тел различной формы. По данным Фруда (переведенным в метрич. меры) для судов сопротивление трения в килограммах выражается ф-лой

R_m=X_cySvh™=О»²⁹⁷³ KySVh*“, где А_с—кеэф., зависящий от длины судна, у— уд. в воды в килограммах/м³, S — смоченная поверхность судна в м², v—скорость судна в м/ск, V—тоже судна в узлах (V=1,944 v); значения коэффициента А_с см. Судостроительный опытовый бассейн. Если подводная поверхность обшита медью, то А_с можно уменьшить на 8%. Если она обросла ракушками, то А_с может возрасти на 30% ^ПР^И увеличении показателя при v до ‘2. При обрастании поверхности водорослями А_сможет возрасти до 50%, но показатель при v не увеличится свыше 1,85—1,90. Из ряда последующих опытов над сопротивлением досок, произведенных с весьма улучшенными измерительными приборами и приемами, следует признать, что цифры, полученные Фрудом, являются заслуживающими полного доверия. Сюда относятся опыты Геберса, Мак-Энти, Тейлора и опыты Национального бассейна в Тед-дингтоне. По данным Геберса сопротивление •трения в килограммах выражается ф-лой

й_м=я^зд(^)^_0’^и5,

где ^—коэфициент, не зависящий от длины судна и равный 0,0103; ρ—массовая плотность воды в килограммах ск²/ж“, v — скорость судна в м/ск, S—смоченная поверхность в м², L—· длина в м, v—кинематическая вязкость в м²/ск; означения ρ и v зависят от t° и равняются:

для морской воды для пресной воды

(	при t°=7°	13°	18° С
	ρ=104,7	104,6	104,5 килограмм ск^/м“
1	г».106 =1,47	1,23	1,08 M^fcK
{	при 4°=0°	10°	20° С
	ρ=101,9	101,9	101,7 килограмм ск^м“
	ν· 106 =1,78	1,30	1,00 м^/ск

Опыты Ксмпфа с трубами дали следующие результаты: а) средняя величина удельных сопротивлений значительно выше соответственных цифр Фруда, Геберса и др. экспериментаторов, б) если исключить из рассмотрения сравнительно небольшую длину (3—6 м) головного участка поверхности (эта длина зависит от очертаний носовой оконечности), то удельное сопротивление остальной части поверхности имеет постоянную величину, то есть не зависит от положения рассматриваемого участка поверхности по длине трубы. Опыты Перринга (1925—26 гг.) показали, что удельные сопротивления хорошо согласуются с данными Геберса, но несколько понижены по сравнению с таковыми Фруда. Опыты Кемпфа на пароходе «Гамбург» (1927 год) дали величины удельного сопротивления, значительно повышенные по сравнению с данными Геберса. В виде“общего вывода можно отметить, что напряженная работа, которая ведется рядом испытательных бассейнов и научных работников, в ближайшее время даст окончательное освещение сопротивления, обусловленного действием касательных сил воды на поверхность судна. В настоящее время является наиболее целесообразным не слишком отходить в вычислениях сопротивления трения от имеющего за собой десятилетия практич. применения метода Фруда, особенно при внесении в него корректив, установленных работами Геберса, Перринга и Национального бассейна.

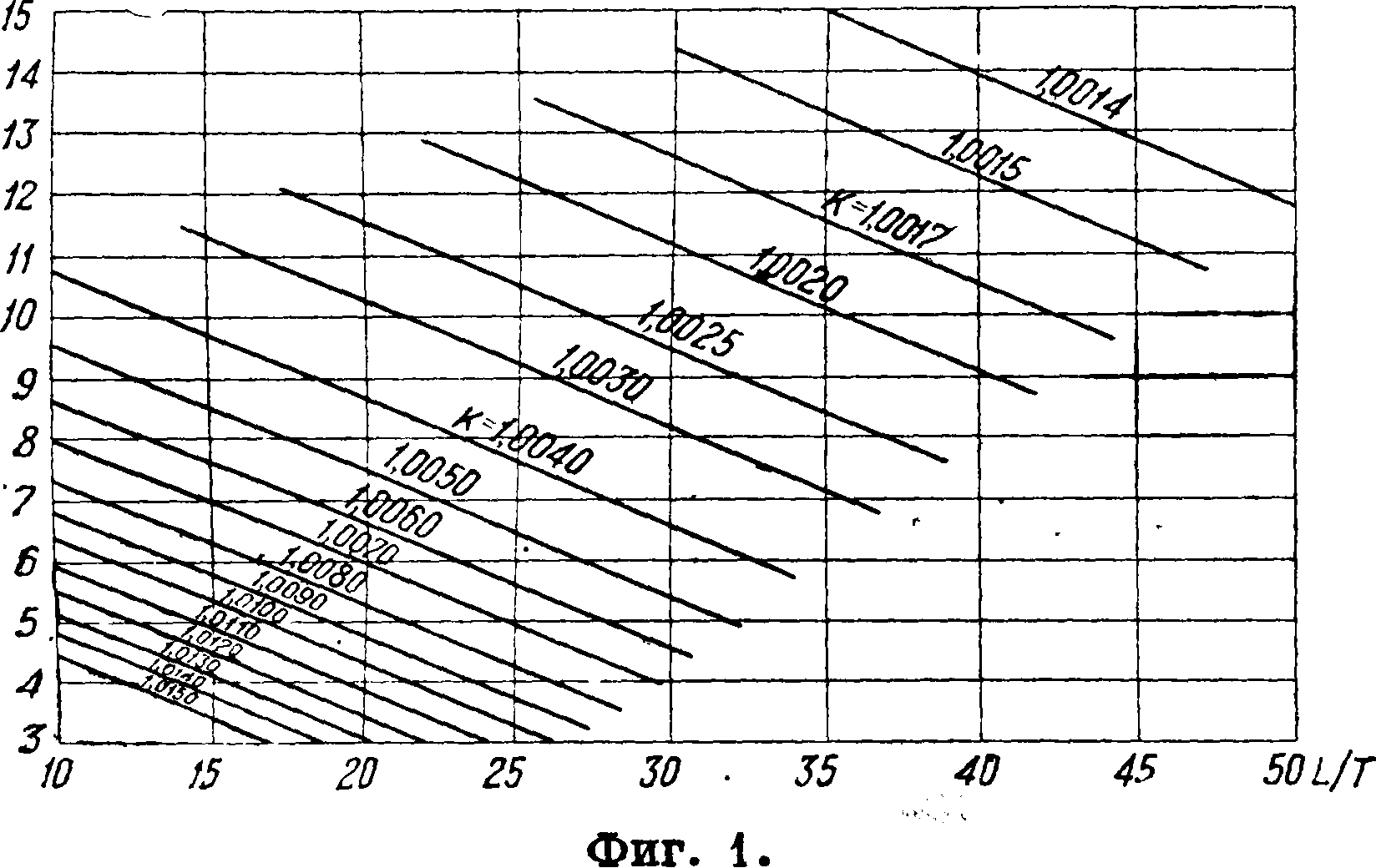
Для определения сопротивления трения необходимо знать величину подводной смоченной поверхности судна. Достаточно точный подсчет м. б. произведен измерением обводов всех шпангоутов от киля по данную грузовую ватерлинию и их суммированием по одному из правил приближенного интегрирования: кривизну поверхности (по Тейлору) учитывают, помножая полученную площадь на коэф. Тс > 1, величина которого в зависимости от отношений L:B и L:T (.В—ширина по грузовой, Т— наибольшая осадка) м. б. взята из диаграммы фигура 1. При проектировании важно знать приблизительную величину поверхности раньше, чем будет изготовлен теоретич. чертеж. В этом случае можно пользоваться одной из следующих эмпирич. ф-л для определения величины смоченной поверхности £ в м²:

8=1,52 LT + (0,374 + 856²)LB (Норман),

$=2L]/g) (Дюпре),

S=Ι/[0,15όΖ7 + 2Т(1 — б)] (Рот),

S=(1,7Т + 6B)L (Мумфорд),

S=уш (Тейлор).

Во всех этих ф-л ах L, В и Т—длина, ширина и углубление судна, D—водоизмещение судна, U—периметр мидель-шпангоута, δ—коэф. полноты водоизмещения {δ=пло щадь мидель-шпангоута. Лучшие результаты дают ф-лы Мумфорда и Тейлора. Значения коэф-та С для ф-лы Тейлора в зависимости от отношения В : Т и коэф-та полноты мидель-шпангоута β м. б. взяты с фигура 2. Подводная поверхность получается в тех единицах, в каких подставляются размеры; при подстановке в формулу Тейлора D в фт.³ и L в фт. получим S в фт.², если же Ό выражено в английских тоннах и L — в футах, то необходимо коэфициент С умножить на 5,92.

Остаточное сопротивление. При обтекании вполне погруженного тела водою

давление последней в носовой и кормовой частях увеличивается, а в средней уменьшается. Если судно не вполне погружено, то свободная поверхность воды подвергается постоянному атмосферному давлению, почему увеличение давления в какой-нибудь точке воды вызывает подъем ее в этом месте выше уровня, а уменьшение давления вызывает образование впадин. Как повышение, так и понижение уровней вы-• зовет образование волн, распространяющихся дальше по закону волновых движений (фигура 3). Характер волн, образуемых носовой и кормо-„ · вой оконечностя щ

0,90

£85

т

£75

	{((	Г	V	tv
1 i	т	L
	у	^£*4.		I	)	)
					у.	у

1,5 2,0 25

3.0 3,5

Фигура 2.

4,0 43 5,0 В/Т

ми-судна, трудно поддается наблюдению, так как при распространении волн, образуемых носовой частью, они смешиваются с кормовыми волнами, почему их вид изменяется. Система волн, производимых движением судна в глубокой невозмущенной воде, состоит частью из поперечных частью из расходящихся волн, угол расхождения которых для одного и того же судна почти не зависит от скорости судна (фигура 4). Расходящиеся носовые и кормовые волны будут взаимно параллельны и нигде .друг с другом не сталкиваются. Поперечные носовые и кормовые волны, наоборот, всегда интерферируют друг с другом. Фруд, изучавший опытным путем эти волны, нашел, что у наклонных волн гребень более крутой, чем у поперечных. Профиль поперечных волн трохоидаль-ный, и длина волны равна длине

•судна. Волны, возникающие на поверхности воды при движении судна, по своему характеру, свойствам и способу распространения не •отличаются от волн, возникающих от ветра. Па основании закона механич. подобия сравнение между естественными и искусственными волнами вполне возможно; для исследований применяется трохоидальная волна, профиль которой образован трохоидой. Теория трохои-дальных волн дает удовлетворительное объяс-

Фигура з. нение всех явлений движения морских волн. Теория была предложена Герстнером и детально разработана Ранкином и Фрудом. Волновое сопротивление судна можно определить по одной из следующих приближенных ф-л:

Д

CD²IЗУ4

_

кз или R_e =

C_XD_X²! 3V4 bi

англ, фн.;

ТУ Λ кю д DV^

R_e=0,518 · —jjT кг или р _-jQ £ dDiV* _

⁶ ~ ^англ· Фн. (Тейлор);

R*=[0,787 + 46,1(9? - 0,53)2] F‘ кз или

Re=[0,53 + 31(9> - 0,53)²] V⁴ англ. фн.

(Ховгард);

обозначения в ф-лах прежние соответственно в англ. (D_x, L_lr В_г, Т_г) или метрич. мерах (2>, L, В, Т), φ — коэф. продольной остроты,

Т а б лУ 1.—3 начениякоэфициентов С и С_х в формуле волнового сопротивления.

Тип судна	С	Ci
Тихоходные грузовые пароходы .. Линейные корабли и «пассажирские пароходы. Крейсеры и быстроходные пассажирские пароходы. Легкие крейсеры и миноносцы ..	0,0616—0,0685 0,0548—0,0616 0,0480—0,0548 0,0411—0,0480	0,45—0,50 0,40—0,45 0,35—0,40 0,30—0,35

Наиболее точный способ определения остаточного сопротивления судна дан Фрудом и состоит в определении волнового сопротивления модели судна и пересчете полученных результатов на натуру. Этот способ основан на законе механич. подобия (смотрите Теория подобия). Он же доказал, что волновые системы судна и его модели при соответствующих скоростях будут подобны. Если отношение размеров судна к модели будет a, a отношение скорости судна к скорости модели У а, то волновое сопротивление судна R_e будет в а³ раз больше такового же для модели, которая должен быть вполне подобна судну как по размерам, так и в весовом отношении, для чего перед буксировкой модели последняя загружается до требуемого веса мешочками с песком. Перед опытом приблизительно определяется наибольшая и наименьшая величины ожидаемого сопротивления модели. Накладывая грузы, соответствующие ожидаемым сопротивлениям, на чашки весов тележки, проводят на бумаге регистрирующего приспособления оси, относительно которых ориентируется кри-

18

Т. Э. m. XXV.

вая сопротивления. Затем с заранее выбранной скоростью буксируется модель (смотрите Судостроительный опытовый бассейн). Когда скорость тележки установится, включаются сопротивление модели и регистрирующие приборы. После пробега на бумаге прибора получится диаграмма (фигура 5), на которой линия а отмечает

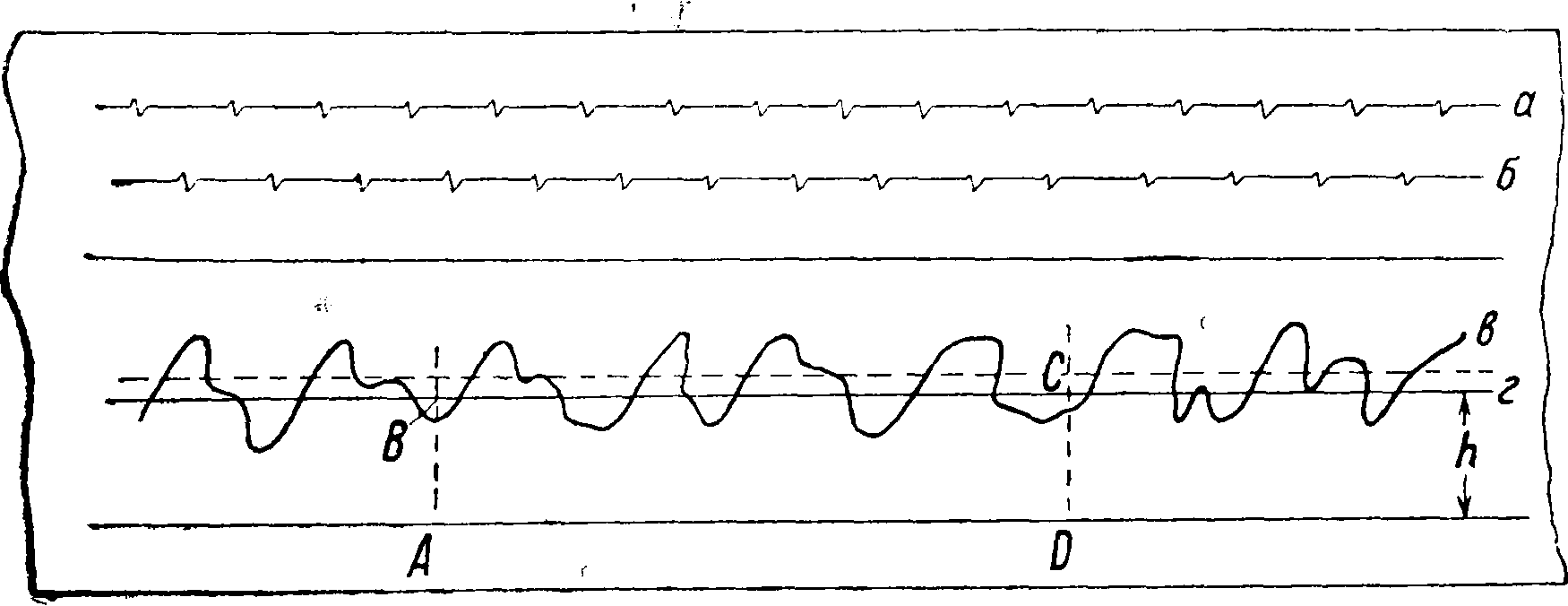
Фигура 5.

путь тележки (обычно через 4 м), б—время (0,5 ск.), а в—сопротивление модели сравнительно с ожидаемым (линия г). Для определения величины сопротивления выбирается часть диаграммы (обычно длиною 32 м) и проводятся крайние ординаты АВ и CD. Планиметром измеряется площадь f прямоугольника ABCD и площадь F, ограниченная осью AD, крайними ординатами АВ и CD и кривой сопротивления в Тогда г=h + Δ/г=h + (ψ) h,

тде h—ожидаемое сопротивление, ΔΗ—разница между истинным и ожидаемым сопротивлением. Получив после ряда пробегов с различными скоростями, включая и максимальную, величины сопротивлений модели, строят кривую сопротивления в зависимости от скорости (фигура 6).

С,

юоо

500

№

то¹-

*0

( -							и/{ /V 1
! > 1						А	/* 1 • : i i i 1 J
- i : ч		* <, - —		в у 1
;		Г ^ 1 1 1	у			<r I	Ly A
		: в ^ у г	- ^		ж!		:
1-	о			Os
ή		а «	6^

1,0 1,2 1.4 1β 1.8 2.0 22 2,4 2,6 2,8 3.0 3.2 3,4 3.6 3.8 4.0v_mm/ch

8 Ю 12 14 16 18 20 22

24

-- 12

Фигура 6.

26 28

Так как закону подобия подчиняется лишь остаточное сопротивление, то из полученного опытом полного сопротивления модели г вычитается сопротивление трения; помножая полученное остаточное сопротивление модели на куб линейного коэф. подобия а³, показывающего, во сколько раз корабль больше модели, · получаем величину волнового сопротивления судна при подобной скорости хода в узлах

V ~ 1,946 v_My а, где v_M—скорость модели в м /ск. Прибавляя к ней сопротивление трения судна, вычисленное по одной из формул, приведенных выше, получаем общее сопротивление судна при данной скорости хода. Основные ф-лы и соответствующие коэф-ты трения судна и модели см. Судостроительный опытовый бассейн.

На фигуре 6 изображена сводная диаграмма испытаний модели и пересчета на натуру миноносца водоизмещением 1 080 т, при "коэф. подобия α= 25; на фигуре 6 обозначают: а—общее сопротивление модели w_m, б—остаточное сопротивление модели, в—общее сопротивление судна W, г—сопротивление трения судна, д—остаточное сопротивление судна, е—сопротивление. * w

судна в килограммах на 1 m водоизмещения ж—мощ ность сопротивления трения в IP, з—мощность волнового сопротивления в IP, и—общая эффективная мощность в IP движителя без учета его кпд, к—адмиралтейский коэф. мощности от

~ D²/sys

водоизмещения <7*=——, где N₀ — общая мощность в Н л и м—диференты носом и кормой при соответствующей скорости хода, А— экономии, скорость хода, В, С и D—скорости, при которых имеет место резонанс носовой и кормовой волн и вследствие этого увеличение сопротивления судна. Путь построения диаграммы следующий: от кривой а откладывают вниз сопротивления трения г_т модели и получают кривую б; увеличивая ее в а³ раз и изменяя масштаб абсцисс в отношении V=1,946^ W получают кривую остаточного сопротивления судна d; прикладывая к ней ординаты вычисленной особо кривой сопротивления трения г, получают кривую общего сопротивления судна в килограммах; помножая каждую ординату кривых б, в и г сопротивлений судна на 0,0006859 V, получают соответствующую мощность в КР. Изменения дифе-рента,наблюдаемые на модели, помноженные на а, дают соответственные значения для судна при подобных скоростях хода. Остаточное сопротивление подвергается достаточно достоверному математическому анализу. Мичель дает аналитическое вычисление его при весьма небольшом круге допуще-£ ний, если только обводы судна I заданы аналитич. ур-иями. Ре-* шение Мичеля в свое время I ускользнуло от внимания спе-циалистов. Лишь после исполь-I зования Гавел оком (1928 год) ме-|*тода Мичеля последний прив-^ лек к себе всеобщее внимание. Виглей (1926 год) приводит кроме ряда теоретич. выкладок, относящихся к методу Мичеля, также результаты фактич. испытаний трех моделей. Общие выводы из опытов Виглея таковы: 1) метод Мичеля дает весьма хорошие количественные результаты; 2) качественный характер кривых чрезвычайно хорошо отвечает действительности; 3) в среднем вычисленные по Ми-челю волновые сопротивления несколько меньше фактически наблюденных величин. Морской инж. Г. Павленко (1928 год) показал, что· метод Мичеля может быть доведен до числового·

ШОО

330000

30

20

я

10*ь

32 34 36 38 40у злоб результата не только для обводов, задаваемых аналитич. ур-ием, но и при обводах, заданных .графически теоретическ. чертежом судна. Объ-. ем требующихся при этом вычислений хотя и, значителен, все же не выходит из привычных для инженера рамок подсчетов, например при под- счетах килевой качки. Отметим, что кривая¹ волнового сопротивления не идет плавно вверх, но с увеличением скорости имеет выступы и -впадины,.обусловленные главным образом ре-¹ зонансом“ и интерференцией носовой и кормо-1 вой волновых систем.

Определение мощности механиз-j м о в Основным вопросом X. является определение мощности механизмов, потребной для, сообщения судну данной скорости. !

Для определения мощности механизмов мо-^г гут служить следующие способы. 1) Способ непосредственного вычисления составных частей мощности. Как, известно, мощность определяется произведением из силы на скорость по направлению силы. Полное сопротивление вычисляется по прибли-женным ф-лам в отдельности для каждого вида сопротивления. Эффективная мощность в ЬР определится ф-лой

N_e=0,00307 R_nV=0,006859jR_wF, где R_n и R_n—полное сопротивление судна в англ, и метрич. мерах. Надежного результата этот способ не дает. 2) Способ адмиралтейских коэ ф-т о в Индикаторная мощность механизмов м. б. определена по одной из следующих ф-л:

N_u =

D²lsvz Сг

У» Ct *

Здесь D—водоизмещение в т, V—скорость в узлах, $$—площадь погруженной части мидель-шпангоута в ж³, Ci—адмиралтейский коэф. от водоизмещения, С₂—адмиралтейский коэф. от миделя. Коэф-ты С_г и С₂ нужно брать из опытов с судами. Применение адмиралтейских коэфициентов может дать надежные результаты лишьлогда, когда судно, взятое для сравне-, ния, подобно проектируемому, причем скорости должен быть соответствующими, то есть находиться в отношении У а. Если брать величину адмиралтейских коэф-тов для судов, сильно различающихся по форме и не при соответствующих скоростях, то получаются ненадежные результаты. Способ адмиралтейских коэф-тов давал хоро-· нше результаты прежде, когда скорости были невелики и не было столь большого разнообразия в типах судов, как в настоящее время. При применении английских мер данные в таблице 2 значения коэф-тов С_г и С₂ необходимо помножить: С_г на 1,0014, С₂ на 10,894. Во Франций находит еще применение адмиралтейский коэф. от миделя, к-рому придается такой вид:

где ш—коэф. утилизации. Значения коэф. С_1е, С* и ш_е для вычисления эффективных мощностей N_e, а также L, D, §£>, F, соответствующие Х_е и — * для ряда судов различных типов приведены в таблице 2. 3) Способ определения мощности по одной из эм-пирич.*ф-л. Для определения мощности механизмов был предложен ряд эмпирических ф-л. Все формулы применимы лишь в пределах тех скоростей, которыми обладали суда в момент вывода их. Приводим некоторые из них.

1. ‘Ф-ла Афанасьева:

Здесь длина: L_x—в фт., L—в ж; водоизмещение: D_x—в англ .тоннах, D—в w; мощность: N_e—в англ. tP, N_e— в метрич. л. с.; F—скорость в узлах; Тс=^ — отношение длины судна по грузовой ватерлинии к наибольшей его ширине; А—практич. коэф. (характеристика),принимаемый для полированных винтов равным 24,5, для неполированных—25. В формуле после подстановки исключается влияние длины судна; последняя играет большую роль в сопротивлении. Для судов водоизмещением до 15 000 тонн и со скоростью до 20 узлов формула дает хорошие результаты.

2. * Ф-ла Ховгарда:

N » 0,00307 10,062 A^FV³ +

+ [0,53 + 31 (φ — 0,53)²] F⁵} англ. IP,

N_e=0,006859 1 0,2973 λβν²,*’* +

+ [0,787 + 46,1 (φ - 0,53)²] ^ F⁵} метрич. л. с.

В ней отдельно учитывается сопротивление трения и волновое сопротивление в зависимости от обводов судна, т. ч. получаются хорошие результаты. Значение букв приводилось выше.

3. Ф-ла Тейлора:

-Ν;= 0,00307 [0,062 λβ_χν* ,³²⁵+12,5 -ЛЛ⁵j англ. IP,

N_e=0,006859 [ 0,2973 A^F²,⁸²³ + 0,518 метрич. л. с.

Значение букв приводилось выше. Формула да-ί ет очень хорошие результаты, если скорость в узлах’ не превосходит УЬ_г фт. Она являет“ ся одной из позднейших по времени появления. 4) Способ испытания моделей. Определив испытанием модели сопротивление ее движению и сделав пересчеты на судно, нетрудно вычислить эффективную мощность, зная, что последняя равна сопротивлению, умноженному на скорость. 5) С п о с о б о пределения мощности по диаграмме Тейлора. Чтобы иметь возможность пользоваться результатами исследований для судов различного водоизмещения, различной длины и при различных скоростях и непосредственно сравнивать их, необходимо привести их к одному показателю водоизмещения, длины и скорости. Для этой цели Тейлор выбрал следующие основные переменные: а) сопротивление выражается в фн. на англ, тонну водоизмещения ^,

б) сопротивление приводится к длине в 100 фт. введением переменной называемой пока-

Ы

зателем длины, в) скорости подобных судов пропорциональны УТ, почему вводится переменная, называемая показателем скорости.

Для вычисления сопротивления трения Тейлор применил формулу Фруда, причем подводную поверхность вычислял по своей формуле (смотрите выше). Одновременно Тейлор дает диаграмму для вычисления коэф-та С в зависимости от отношения

Таблица 2. — Значения коэфициецтов сопротивления и основные данные судов различных типов.

Λί	Тип судна	L в м	D в т	В м“	У в узлах	Ne в IP	Ne D	C2e	Cie	me
1	Трансатлантический экспресс.	280,0	57 700	322,0	23,2	61 800	1,07	65	302	4,02
2	» ».	202,0	22 900	166,5	23,5	37 800	1,65	61	298	3,94
ул		190,5	21 385	148,7	22,0	27 000	1,26	64	327	4,00
4	Большой паесаширский пароход	194,0	22 100	165,0	18,0	17 200	0,78	60	287	3,93
5	» » »	193,0	23 200	165,8	15,0	9 300	0,40	65	315	4,02
6	» » »	170,0	17 250	139,6 125,3	18,5	10 Р00	0,61	64	305	4,00
7	» » »	136,5	13 175		13,5	4 800	0,36	69	308	4,10
8	» » »	121,4	10 340	114,2 44,3	11,5	2 500	0,24	77	322	4,25
9	Малый пассажирский пароход.	69,5	2 200		10,0	1 050	0,48	50	190	3,68
10	Пассажирский пароход для перевозки через Ламанш.	92,0	1 915	32,3	20,0	5 600	2,92	46	220	3,59.
11	Пассажирский павоход для перевозки через Ламанш.	83,8	1 695	33,2	20,0	5 400	3,19	49	211	3,66
12	Паровая яхта..	121,9	5 710	63,7	15,0	3 700	0,65	61	307	3,97
13	» » ..	116,6	4 260	65,3	21,5	9 650	2,27	72	291	4,16
14	Большой грузовой пароход.	170,7	24 800	178,0	13,5	5 460	0,22	86	418	4,43
15	» » »>.	152,4	21 115	163,0	12,0	4 000	0,19	76	359	4,23
16	» » ».	131,1	12 400	115,4	11,0	2 500	0,20	69	316	4,10
17	» » ».	105,2	7 985	89,7	11,0	1 700	0,21	80	357	4,31
18	Малый грузовой пароход.	88,1	4 580	63,1	10,5	1 225	0,27	70	305	4,12
19	» » ».	79,8	3 400	59,9	9,0	700	0,21	76	288	4,23
20	» » ».	62,1	1 760	37,3	9,0	440	0,25	79	307	4,29
21	» » ».	47,3	940	29.4 18.5	8,0	350	0,37	55	181	3,80
22	» » ».	37,8	320		9,0 12,0	280	0,81	50	172	3,68
23	Малый каботажный пароход.	32,0	130	6,9		225	1,73	71	263	4,14
24	» » »	26,0	68	4,1	12,0	220	3,33	43	172	3,50
25	Промысловый пароход.	41,0	445	17,0	10,9	490	1,10	57	194	3,85
26	Буксирный пароход.	40,0	390	17,2	11,0	350	0,90	84	262	4,38
27	» ».	35,0	340 ;	16,1	12,1	520	1,53	67	203	4,06
28	» ».	15,2	48	5,2	9,1	150	3,13	36	91	3,30
29	Ледокол..	47,2	890	29,8	9,5	500	0,56	64	200	4,00
ВО	Речной товарный винтовой паро-ход ..	60,0	481 :	9,4	7,3	205	0,43	24	156	2,88
31	Речной колесный пассажирский пароход ..	62,0	325	7,1	9,9	503	1,55	18	114	2,64
32	Речной колесный пассажирский пароход ..	40,5	100	3,2	11,1	250	2,50	24	157	2,88
33	Речной колесный товарный пароход ..	67,0	550	9,3	7,2	382	0,69	12	85	2,29
84	Речной колесный буксирный пароход ..	50,0	300	7,3	10,3	620	2,07	16	98	2,52
35	Речной колесный буксирный пароход ..	40,0	212	6,9	10,5	300	1,42	35	179	3,27
33	Речной пароход с кормовым колесом ..	46,8	144	3,8	9,0	210	1,46	17	128	2,57
37	Речной пароход с кормовым колесом ..	22,8	43	2,4	8,0 1	80	1,86	24	125	2,88
38	Паровой баркас ..	15,0	23	2,6	8,0	65	2,83	32	107	3,17
39	Линейный корабль.	175,3	26 000	239,8	22,1	46 000	1,78	56.5	205	3,83
40	Большой крейсер..	193,8	24 000	222,7	27,5	63 000	2,62	73,5	275	4,18
41	Малый крейсер..	140,5	4 900	60,9 ‘	28,0	30 000	6,07	45,0	213	3,55
42	Большой миноносец.	101,8 76,3	1800	27,7	35,7	40 000	22,2	31,6	168	3,16
43	Малый ».		700	11,6	82,5	20 Ό00	28,6	25,0	135	2,93
44	Подводная лодка над водой.	82,0 82,0	1 128	22,0	14,7	2 400	2,13 0,59	29	143	3,08
45	» » под ».		1863	36,7	8,5	1 100		20	84	2,74

и коэф-та полноты миделя μ или В зави-

ш

симости от изменения μ и отношения ~. Для вычисления сопротивления трения для судна Тейлор дает диаграмму, в которой в зависимости от показателя скорости и показателя дли нны, _г можно непосредственно получить со-

(ϊδό)

противление трения на 1 англ, тонну водоизмещения для судна в 500 фт. длиною. Остальные размеры и характер обводов при этом таковы, что коэф. С получается равным 15,4. Если G имеет другое значение, определяемое из диа-гоаммы, то вводится поправочный множитель. Так же поправочный множитель вводится, если Судно имеет длину, отличающуюся от 500 фт.

Таким путем определяется. Для определения величины остаточного сопротивления Тейлор взял нормальный (стандартный) теоретический чертеж. Исходя из него, было изготовлено

80 моделей, причем изменились отношение ~

показатели длины и коэф. продольной

νϊόο)

остроты φ. Отношений у было взято 2, именно

2,25 и 3,75. Каждая из 80 моделей была испытана в бассейне, и остаточное сопротивление в фн. на англ, тонну водоизмещения было дано в диаграммах. Каждая диаграмма остаточного сопротивления дана для определенного отно-В V

шения γ- и. Кривые на ней дают значения сопротивления для целого ряда значений коэф-та продольной остроты φ и отношений

* встречаемых на практике. Для применено)

ния кривых при отношениях, отличающихся &г приведенных на диаграммах, применяется интерполяция, что заменяет испытание промежуточных моделей. Имея из диаграммы значения R_m

сопротивления трения =~ и остаточного сопро-R

тивления — на англ, тонну водоизмещения,

нетрудно вычислить и полное сопротивление. Для перехода от сопротивления к мощности в англ. ЕР вводится множитель 0,00307DV. Теория Тейлора и его диаграммы изложены в его ценном труде D. W. Taylor, The Speed and Power of Ships. Пользование диаграммами Тейлора дает почти такую же точность определения мощности механизмов, как и испытания в бассейне модели. Применять этот способ нужно с некоторой осторожностью, обращая внимание на пределы допущений и учитывая некоторые недостатки его, так как наилучшие результаты получатся для тех судов, которые более или менее похожи на прототипы, испытанные Тейлором. Способ незаменим при первоначальных прикидках мощности, а также при проектировании судов в институтах, когда испытание моделей вследствие материальных затруднений невозможно.

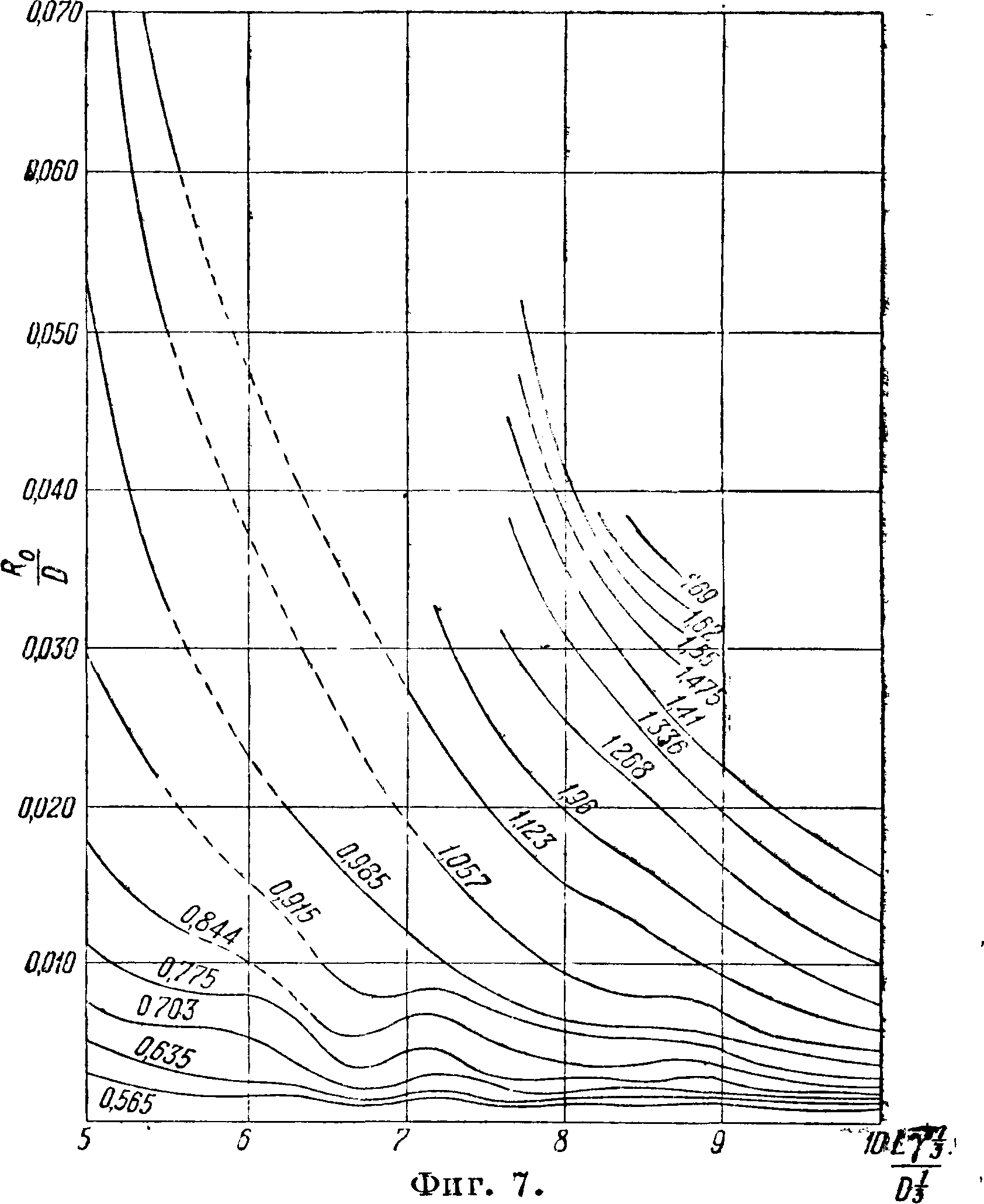
На фигуре 7 приведены (по Ch. Боуёге’у) кривые остаточного сопротивления в ш на одну т водоизмещения ίττ) в зависимости от остроты

V^D _т ι/о

----______________ ^LV ⁸ Л ,__.

судна, выражаемой отношением

(где у—

уд. в воды, равный 1,00 для пресной’и 1,02-у1,03 для морской воды) для различных значений подобных скоростей w(#³D)“^1/6·

Зависимость сопротивлен и ясу д-на от основных размерений судна. Коэф. трения А_с и показатель степени п уменьшаются с увеличением длины судна в весьма незначительной мере. Поэтому сравнительно тихоходным судам, для которых доминирующее значение имеет сопротивление трения, придают меньшую длину, так ка с при этом уменьшается величина смоченной площади S. Остаточное сопротивление при равном водоизмещении уменьшается с увеличением длины. С увеличением скорости влияние длины увеличивается, что приводит к росту длины у быстроходных судов несмотря на то, что это вызывает увелиг чение сопротивления трения. Т. к. сопротивление трения пропорционально квадрату скорости, а остаточное сопротивление пропорционально четвертой степени скорости, то экономия в остаточном сопротивлении для более длинных судов при больших скоростях поглощает увеличение сопротивления трения. При достижении некоторого предела (около 250 м) полное сопротивление начинает увеличиваться с увеличением длины. Рост скорости у современных, особенно военных, судов вызывает увеличение их длины. Но по ряду соображений этот рост длины ограничивается в сравнении с ростом скоростей. Увеличение относительной скорости, характеризуя сравнительное укорочение судна, свидетельствует о том, что сопротивление современных судов приближается к наиболее невыгодной области в отношении достижения скорости, то есть к горбу кривой сопротивления. Стремление к достижению больших скоростей заставило конструкторов обращать наибольшее внимание на уменьшение остаточного сопротивления. Первым способом является заострение оконечностей, вторым— введение цилиндрич. вставки в средней части судна. При малых скоростях введение такой вставки всегда уменьшает остаточное сопротивление. При больших скоростях вставка вызывает увеличение остаточного сопротивления, а для средних, скоростей для ^т аждого коэфициен-та продольной остроты φ имеется такая длина вставки, которая отвечает минимальному остаточному сопротивлению. Еще В. Фруд установил, что носовые шпангоуты должны иметь форму U, а кормовые форму V. Опыты Тейлора подтвердили выводы Фру да. Образующееся при движении судна вокруг носа повышенное давление, сосредоточенное благодаря U-образным шпангоутам глубоко под водой, в большей степени направляет струи воды под днищем· к корме в область пониженного давления для заполнения пространства за кормой и в меньшей степени к поверхности. Вследствие этого при U-образных носовых шпангоутах получается меньшее волнообразование. Широкая плоская корма способствует этому движению струп под днищем. U-образные кормовые шпангоуты, как показали опыты, менее выгодны, чем шпангоуты V-образной формы, а также и чем

плоская корма. Для малых скоростей (до F «0,6УТ)> когда волновое движение не имеет существенного значения, выгода U-образного носа менее ощутима, т. ч. судно с подрезанным носом и расширяющимися носовыми шпангоут тами V-образной формы показывает лучшие, результаты.

В последнее время начинает применяться каплеобразная форма носа. Эта форма была впервые предложена также В. Фруд ом, к-рый подобным утолщением крайней носовой оконечности создавал фальшивую носовую волну, в подошве которой должен был локализоваться гребень главной носовой волны, чтобы добиться хотя бы частичной нейтрализации носового волнообразования. Каплеобразная форма носа является развитием U-образования носовых шпангоутов, поэтому имеет все те преимущества в смысле направления струй под днищем к корме, какие отмечались выше. Положительное влияние каплеобразной формы носа наиболее ощутимо при скоростях (1,0-5-1,2)!/L, причем уменьшение сопротивления достигает до 10%. Капля должна помещаться ниже грузовой ватерлинии вблизи киля; выше грузовой форштевень м. б. прямым вертикальным. На последних герм, и итал. военных кораблях применена каплеобразная форма носа. Точно так же на цовейших трансатлантических пароходах «Бремен» и «Европа» имеется капля (смотрите Судостроение). С увеличением отношения ширины судна к углублению от 1,79 до 4,0.3 увеличивается и полное сопротивление в зависимости от скорости в пределах 15-Ξ-25%. Увеличение углубления влечет уменьшение смачиваемой поверхности, а следовательно и сопротивления трению, но при условии, что это увеличение не связано со значительным уменьшением длины, т. к. при этом выигрыш на сопротивлении

Фигура 8.

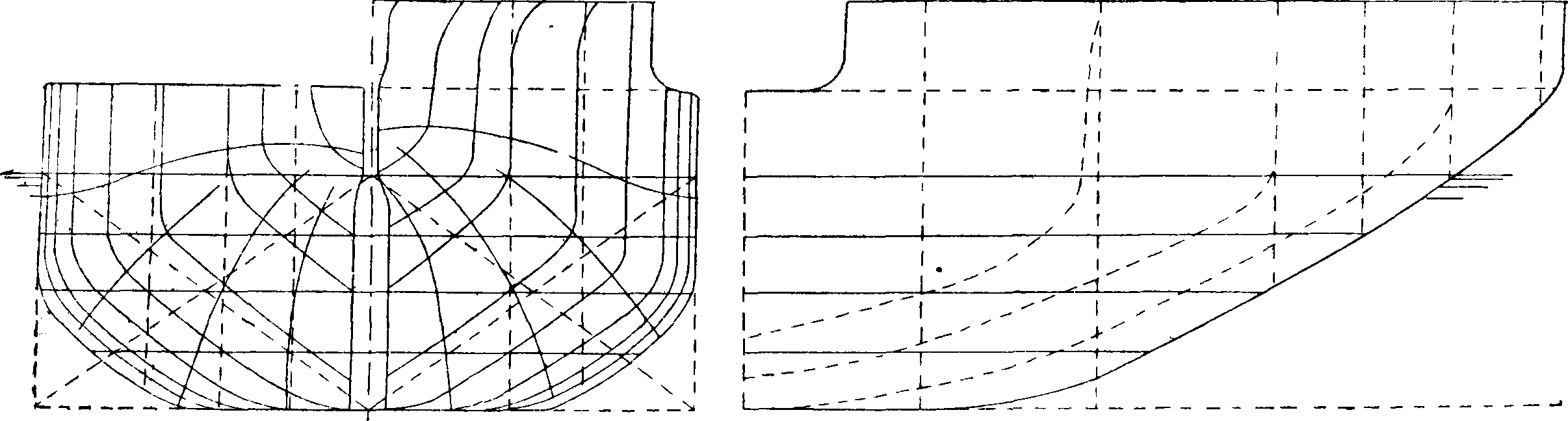
тренйя поглотится потерей на остаточном сопротивлении. Остаточное сопоотивление уменьшается с увеличением углубления. Диферент судн& на корму имеет положительное влияние на сопротивление, хотя размеры этого влияния невелики. Это влияние объясняется улучшением обтекания поверхности наклоненного на корму судна. Вместе с тем диферент на корму способствует лучшей работе винтов. В последнее время начала применяться особая форма подводной части судна, предложенная еще до начала империалистической войны инж. Майёром. По данным Гамбургского бассейна она уменьшает полное сопротивление до 20%. На фигуре 8 показаны проекции струй на корпусе для нормальных обводов. Струи имеют искривленную форму и благодаря этому путь частиц водь! вдоль судна увеличивается, вследствие чегб увеличивается сопротивление трения. Энергия же, необходимая на отклонение струй от кратчайшего пути, увеличивает и полное сопротивление. Придание судам таких обводов, чтобы струи были возможно спрямлены и частицы воды шли по кратчайшим путям, должно привести к уменьшению сопротивления. Из фигура 9 видно, что при обводах Майера струи значительно спрямлены. Все шпангоуты в фор

Фигура 10.

Фигура 9.

ме Майера параллельны между собою и наклонны по всей длине на один угой. Кормовая и носовая половины симметричны между собою. Ц. т. отдельных половин шпангоутов должны находиться по возможности на одной йрямой, причем проекции носовой и кормовой половин ее на корпусе должны совпадать^ Кроме спрямления и укорочения струй форма Майера имеет еще следующие преимущества. Подводная¹ .поверхность уменьшается до 7%, чтй влечет за собою уменьшение сопротивле ния трения. Особенное значение имеет форма форштевня в связи с треугольной формой шпангоутов, которая создает благоприятные условия для входа носа в воду и уменьшает волнообразование в носу. Обычная для нормального судна водяная гора впереди его форштевня у формы Майера отсутствует почти совершенно. Кормовые волны также значительно меньтне. Остальные мооеходные качества судна, имеющего обводы Майера, также повышаются. Кроме того простота форм шпангоутов и уменьшение числа листов наружной обшивки с поверхностью двоякой кривизны облегчают постройку судов с этими обводами.

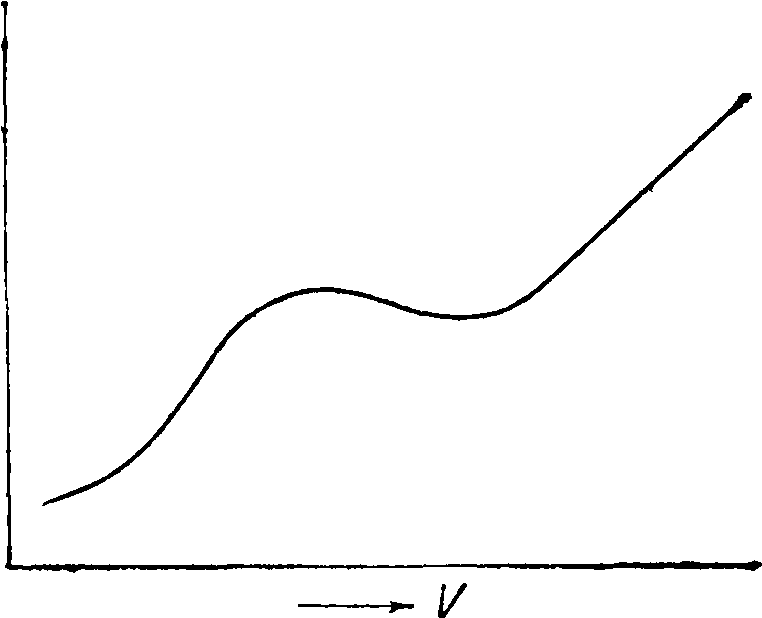
Суда быстроходные и глиссирующие. При скоростях F^1,5[/.L происходит наложение вершин носовых и кормовых волн, вызывающее увеличение волнообразования, а следовательно и сопротивления. Но за этим пределом система носовых волн, удлиняясь, продвигается в корму и начинает постепенно интерферировать с кормовой системой, т. ч. высота волн за кормою начинает уменьшаться. Пока это уменьшение не будет поглощаться ростом расходящихся волн, относительное полное сопротивление будет уменьшаться. Кривая полно-го сопротивления примет вид, представленный на фигуре 10. Чем длиннее носовая часть корпуса и более пологи линии батоксов, тем меньше влияние расходящихся волн и тем резче скажется влияние интерференции поперечных волн. Большое значение при больших-скоростях имеет форма кормовых батоксов. Пологая их форма создает хороший подвод струй воды к винтам. С возрастанием скорости от V == 2,5]/ь до F=4,0ΥΈ единственным средством для уменьшения сопротивления является уменьшение волнообразования вообще. Для этого необходимо, чтобы поверхности встречи с водой имели возможно удобные пологие углы и наименьшую кривизну обводов, по которым направляются естественным ходом струи воды. У глиссеров (смотрите) эти струи направляются вдоль батоксов и скулы. Плоские пологие батоксы для глиссеров необходимы, подъем же батоксов в корме нежелателен, т. к. это вызовет всасывающее действие кормовых обводов, увеличение попутного потока, а следовательно увеличение сопротивления. Во всех судах струи воды, направляющиеся под днище в корму, дают вертикальную составляющую, действующую снизу вверх на днище судна. Для глиссеров с увеличением скорости вертикальная составляющая принимает значительную величину, и если обводы судна имеют соответствующую форму для ее использования, то судно поднимается из воды,т.ч. вес вытесняемой им воды меньше его веса. Использование глиссеров для военных целей побудило все морские державы усиленно заняться этим родом судов и добиться за короткий срок больших результатов. Но это же обстоятельство заставля т держать в строгой тайне достижения, так что в литературе найти указания относительно формы и зависимости между их элементами невозможно. Полное сопротивление буксируемой под различными углами диферента пластины уменьшается по мере его увеличения, достигая минимума при 4—6°, а затем растет, ассимпто-тически приближаясь к некоторой прямой. Бекер дает зависимость между водоизмещением d_± в англ. фн. (Я в килограммах) модели, площадью несущей поверхности в кв. фт. (s в м²) и скоростью v_x в фт./ск. (V в м/ск) в форме ур-ия:

= 0,12vf; —=6,3г>².

Формулировка наиболее точна в пределах най-выгоднейшего угла встречи, то есть 3—5°. В отношении дореданной части глиссера имеются 2 противоположных требования: она должна улучшать глиссирующие его свойства и удовлетворять требованиям мореходности. Для первого необходимо наиболее плоское образование днища, т. к. вертикальная составляющая получается больше, достигая максимума при совершенно плоском днище. Мореходные же качества плоского образования неудовлетворительны. Необходимость разрезания и разбрасывания на стороны встречной волны, требования сухости палубы глиссера при этом и его устойчивости на курсе приводят к заострению днища внизу с развалом наверху у палубы, что не вяжется с требованиями глиссирования. В противоположность носовой зареданная часть может быть вполне плоской. Относительно формы и высоты редана нет определенных данных. Имеются лишь указания, что форма редана должна обеспечивать свободный доступ воздуха в реданный угол для выхода глиссера на редан. Расположение зареданного днища должен быть таково, чтобы достигалось наименьшее обрызгивание его струями воды, срывающимися с редана. Вычисление сопротивления не имеет той определенности, как для обычных судов. До выхода на редан величина сопротивления определяется так же, как и для обычных судов. К моменту выхода глиссера на редан сопротивление достигает максимума, и движение его принимает толкущийся характер. С переходом в глиссирующее состояние наступает успокоение в движении/и величина сопротивления оказывается пропорциональной скорости в степени <2.

Лит.: Погодин А., Судовые двигатели, СПБ, 1908; Ф а н-д е р-Ф лит А., Теория корабля, ч. 2, СПБ, 1913; Костенко В., Теория корабля, Сопротивление воды движению судов, Л., 1926; Найденов В., Теория корабля, Сопротивление судов, Одесса, 1928 (лит.); Яковлев С., Кораблеустройство и трюмное дело, ч.1.—Теория корабля, Л., 1928; Харитонович Б., Сопротивление воды движению судов, Л., 1931 (лит.); Pollard J. et Dudebout A., Architecture nasale, Theorie du navire, t. 1 — 4, Paris, 1890 — 94; Froude W., Experiments on Surface Friction Experienced by a Plan Moving through Water, «Br. Ass. Rep.», L., 1874—1877; Rankine M., On Plate Water-Lines in Two Dimensions, «Transactions of the Institution of the Naval Architects», London, 1864; Taylor D., On the Ship-Shaped Stream Forms, ibid., 1894; Taylor D., The Speed a. Power of Ships, v. 1—2, N. Y., 1910; Havelock T., Theory of Ship Waves a. Wave Resistance, «Proc. Roy. Soc.», L., 1908, 1925; Baker G., Ship Form Resistance a. Screw Propulsion, 2 ed., L., 1920;

T e 1 f e r E., Ship Resistance Similarity, «Transactions of the Institution of the Naval Architects», 1927; Perrins: <r., Some Experiments upon the Skin Friction of Smooth ^Surfaces, ibid., 1926; W i g 1 e у W., Ship Wave Resistance, ibid., 1926; T u t i n J., The Analysis of Ship Resistance, ibid., 1928; Ni со Ison D., Design a. Construction of High-Speed Motor Boats, ibid., 1927; M i-c h e 11 J., «Philosophical Magazine», L., 1898; D о y-*e r e Ch., Contribution & l’6tude de la resistance h la marche d*un navire, P., 1918; G e b e r s F., Ein Beitrag zur experimentellen Ermittelung des Wasserwiderstandes igegen bewegten Korper, «Schiffbau», В*., 1908; К e m p f <G.* Neuere Erfahrungen im Schiffsbau-Versuchswesen,

Jahrbuch der Schiffbautechn. Gesellschafy В. 26, В., 1927; Horn, Theorie des Schiffes, Hndb. d. physikalischen u. technischen Mechanik, hrsg. v. F. Auerbach u. W. Hort, B. 5, 2 Aufl., Lpz., 1928; J о h о w-F о e r s t e r, Hilfs-buch fur den Schiffbau, В. 1, 5 Aufl., B., 1928; многие статьи журнала «Werft-Reederei-Hafen», В. С. Яковлев.