Центр инерции

Центр инерции, центр масс, системы точек, точка приложения всех внешних сил, действующих на систему, когда она помещена в равномерном динамич. поле. Таким образом Ц. и. является центром параллельных сил, действующих на точки системы, и следовательно положение Ц. и. системы точек не зависит ни от напряжения поля ни от положения Системы в этом поле. Координаты Ц. и. системы точек имеют вид:

	ΣτПХ
	ΊΓ
II	Σmy
II	М
	Σmz
*с =	~ΊΓ

(1)

где М—масса всех точек системы; для однородного тела

Σνχ

~V~

Ус-

Ivy

(2)

Σνζ ~V~,

то есть положение Ц. и. однородного тела не зависит от его плотности.

Закон движения Ц. и. Ур-ия движения точки с массой т_х имеют вид:

(3)

d²^!

^mi -ЩГ

= Sl+Cl

где X_l9 Y i, Z_t—проекции на координатные оси внешней силы, приложенной к точке, Ii,

Ci—проекции внутренней силы (или равнодействующей всех внутренних сил), приложенной к точке. Суммируя ур-ия движения системы точек относительно оси ж-ов, имеем:

Σ»*^=ΣΧ + ΣΙ (4)

или т. к. массы тбчек не зависят от времени, то

-£ϊΣμ*=ΣΧ+Σ*·

Но из (1) %тх=Мх_е; кроме того Σί=0 как сумма проекций на ось ж-ов всех^ внутренних сил системы. Аналогично Σ*7=0, ΣC=0. Следовательно

d²x_e

di²

= ΣΧ

d²y_c

dt²

= ΣΥ

d*z_c

dt^

= ΣΖ

(5)

Из сравнения последних ур-ий с ур-ием (4) видно, что Ц. и. системы точек движется так,

как если бы в нем была сосредоточена вся масса системы и к нему были приложены все внешние силы. Из ур-ий (5) следует, что внутренние силы не влияют на движение Ц. и., например давление пара как сила внутренняя по отношению к паровозу не может вызывать перемещения Ц. и.- паровоза. В частном случае если ΣΧ=ΣΥ — ΣΖ=0, то, интегрируя уравнения (5), получаем

®_c^==aiⁱ+ С_г )

Ус=a_gt + С_ч >· (6)

&с — 4* С₃

Т. о. если нет внешних сил, то центр инерции системы движется прямолинейно и равномерно. См. Масса и Механика теоретическая.

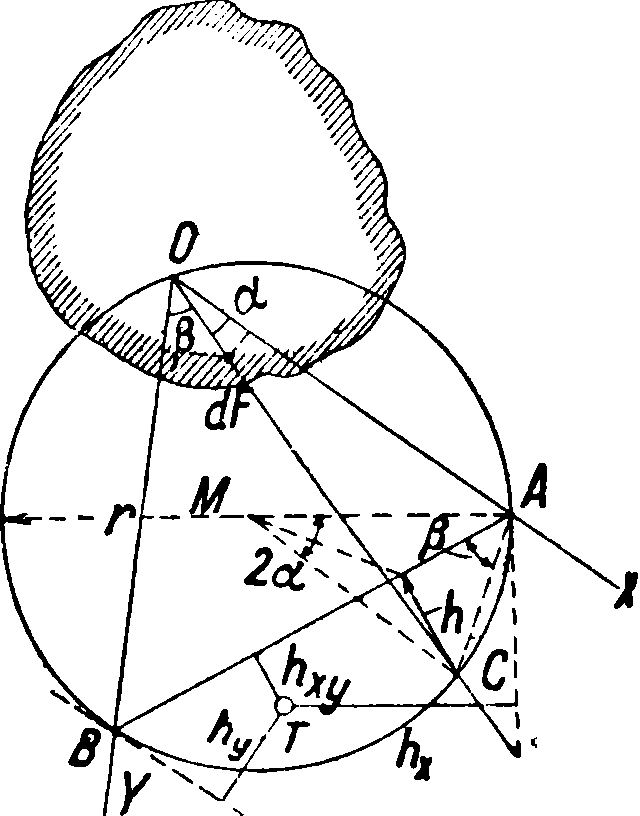
Графическое определение Ц.и.По отношению к осям ОХ и О Г (смотрите фигуру) центробежный момент инерции для элемента dF сечения будет

!_ху=f х У · dF.

Если через О и dF провести луч, то центробежный момент инерции можно выразить так:

1_ху=J ρ² · sin α · sin β · dF,

где ρ—расстояние от dF до О, а и β—углы, образуемые лучом с координатными осями. Если из произвольного центра М провести через О окружность, то перпендикуляр h, опущенный из С на хорду АВ, выразится:

h=2г · sin а · sin β

(А, В и С—точки пересечения окружности с осями координат и лучом). Т. о.

Подинтегральное выражение можно рассматривать как статич. момент относительно оси

АВ элементарной силы

· dF 2 г сосредоточен ной в точке С окружности. Если Т—точка приложения равнодействующей всех этих сил для всего поперечного сечения F, а Ь_ху—расстояние ее до хорды АВ, то

ρ2. dF

h -

¹¹ ху 2 ’

,у, 1_ху превра-

1_у. Положе-

^xy—^zyj 2 г где 1₀—полярный момент инерции площади F относительно точки О. Точка Т приложения всех элементарных сил данной площади, перенесенных на окружность, есть Ц. и. Выведенное ур-ие справедливо при всяком положении осей, следовательно и для случаев, когда одна из них приходит к совмещению с другой, причем хорда АВ переходит в касательную в точке А или В, h_xy переходцт в h_x или h щается в моменты инерции 1_Х или ние Ц. и. Т при этом не меняется, т.“к. зависит только от формы площади F, положения центра М и диаметра окружности. Т. о.

I_x= f у² dJ?=J* ρ² sin² a dF=h_x · ^

Ί —h · ~

¹y~^rty _ir>

где h_x и h_y—соответственно расстояния центра инерции от обеих касательных в А и В. Если взять 2 г=1₀, то

f-ху ⁼ ^ху, Ιχ К

1у — hy.

Итак, при данных 1_Х, 1_у, 1_ху Ц. и. находят, описав из произвольного центра радиусом г=£1₀

окружность, проходящую через точку О. Особенное упрощение получается, когда обе оси ОХ и OY перпендикулярны друг к другу. Тогда 1₀=1_х + 1у, хорда АВ проходит через центр“ М окружности, h_x и h_y—параллельны этому диаметру. Определение положения главных ОСеИ ИНерЦИИ-см. Момент. в Никаноров.

Лит.: см. Масса, Момент и Механика теоретическая.