 > Техника, страница 91 > Центр тяжести
> Техника, страница 91 > Центр тяжести
Центр тяжести
Центр тяжести системы материальных точек, точка приложения равнодействующей сил тяжести, приложенных ко всем точкам системы. Ц. т. системы точек является центром параллельных сил, пропорциональных массам материальных точек, поэтому помимо основного термина употребителен и "другой— центр масс. ВЦ. т. системы считается сосредоточенной вся ее масса без изменения момента системы относительно любой оси (для плоской линии и фигуры) или любой плоскости.
Если тело представляет систему конечного числа материальных точек, то вес тела выразится
Р=Σ pi,
где р^—сила тяжести, приложенная к произвольной частице тела. Для определения положения Ц. т. твердого тела могут служить ф-лы для координат параллельных сил:
х =
Σ Р?*г _ Σ Ргхг ·
у=-
Σ Рг ViVi
Z =
УгЧ
р > ~ р ’
где Xi, у i, Zi—координаты любой частицы твердого тела. Если —бесконечно малый объём частицы тела, то плотность у тела в данной точке выразится так:
7 Δ vi
откуда Ρι=γ · Δ Vi и в случае однородного тела
Ρ=Σ р“= Σ у Δ Vi=у Σ tyi=yV (V—объём тела). Предыдущие ф-лы преобразуются в следующие:
Σ piXi Σ XiY · Avi у · Σя/Δυ* Σ XiAvi
_ ___ у ’
X=·
z=-
yV
Σ 2 i Αν .·
VV
— _
У — γ
следовательно Ц. т. однородного тела м. б. назван Ц. т. объёма.
С понятием Ц. т. твердого тела связаны понятия Ц. т. поверхности и Ц. т. линии. Выделив бесконечно малый элемент Δ$г- поверхности, выразим поверхностную плотность его:
(рг—вес элемента поверхности), откуда р, =·=у. Δsi9 а вес всей однородной поверхности
Р-bр.-bг&.-пbЬ.-г“
(S—площадь всей поверхности). Для определения координат Ц. т. поверхности будут служить ф-лы:
Σ р/Χι _ Σ угХ/Asi _ γ Σ χ,-Asj _ Σ XjAsfYiS
X=-
S
Σ ζ,-As
Для определения Ц. т. линии выделим элемент ее Mi весом рг·; линейная плотность его у - Vi-
Так как откуда после преобразований ф-лы для определения Ц. т. линии получают следующий вид:
— _ Σ XjAlj + _ Σ у [Ali ~ _ Σ Z/Alj X~~Z = ~~L ’
где L—длина лйнйи.
f Вспомогательными теоремами при определении Ц. т. служат следующие.
1) Если данный объём (поверхность, см линия) имеет плоскость симметрии, то
Ц. т. лежит в плоскости симметрии.
2) Если данный объём (поверхность, линия) имеет ось симметрии, то его Ц. т. лежит на оси симметрии. 3) Если данный объём (поверхность, линия) имеет центр симметрии, то его Ц. т. лежит в центре симметрии. 4) Если данный объём (или поверхность) состоит из нескольких частей,
— то Ц. т. может быть опре-
__±1_х делен как Ц. т. нескольких к— Зсм—я материальных точек, полу-
Фигура 1. чаемых, если сосредоточить вес каждой отдельной части в ее Ц. т., например Ц. т. уголка (фигура 1) определится сл. обр.:
- _ 8 -0,5+ 2.2 ~ 8 + 2
= 0,8 см,
У
8-4 + 2 «0,5 3 3
8 + 2
СМ.
Применим методы интегрального исчисления к нахождению сумм ΣχΑν?· При мер 1. Найти Ц. т. дуги, составляющей четверть окружности (фигура 2). Если х2 -f у2=а2 «есть ур-ие окружности, то и отсюда
dl=Ydx2 -f dy2=a- dx
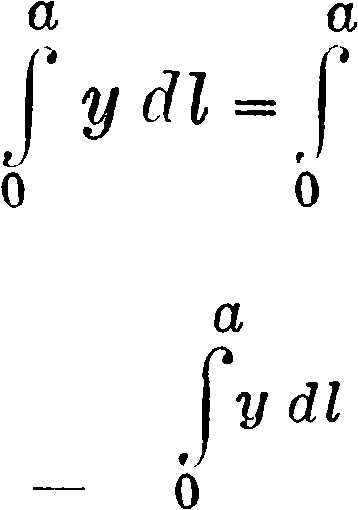
У- —
У -ydx=a2,
«2 _ 2 a πα π
ΊΓ
То же значение имеет с Пример 2. Найти Ц конуса, плотность которого возрастает про-
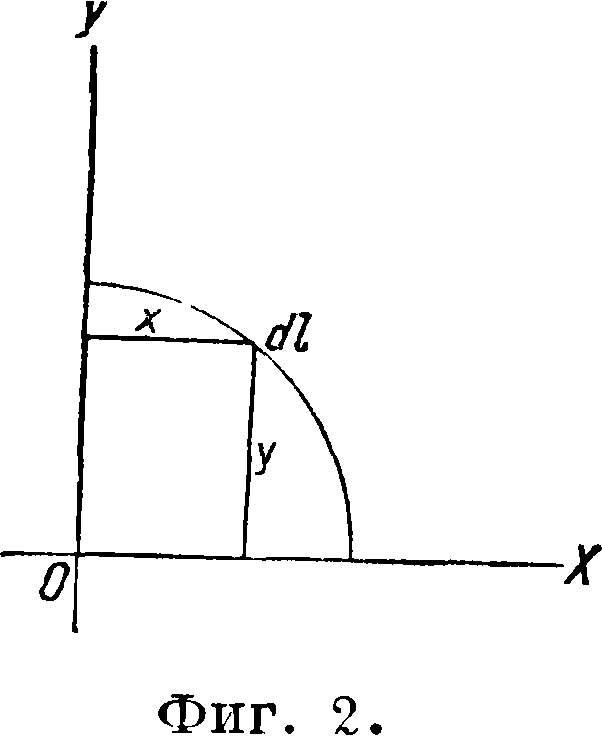
с (в виду симметрии). т. прямого круглого
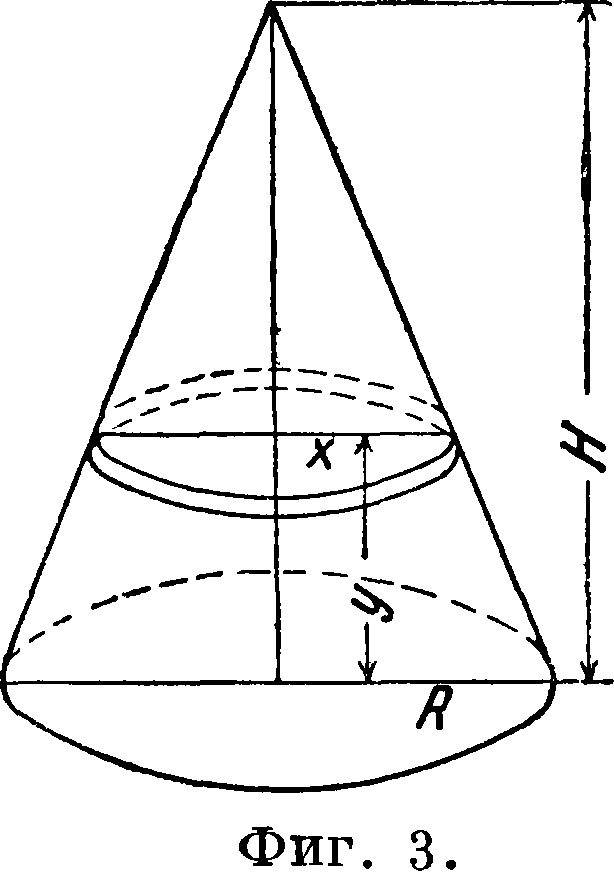
порционадьно расстоянию слоя от основания (Н — высота конуса, R — радиус основания). Разделив конус на слои, параллельные основанию, рассмотрим слой на расстоянии у от основания (фигура 3). Отбрасывая бесконечно малые высших порядков, примем объём слоя равным nxldy, а плотность его равной ку, где к=Const. Т. о. масса слоя
dm=кпх2 у dy.
ТО
J ydm=-j-
knR 2 /τι Λ2 2 τ knRZH2
(H-y)2y2dy =
Я2
30
Η
Μ=J dm=J (H- yf у dy =
hnmm
12
Следовательно
У =
dm
M
=lH-
В нек-рых случаях Ц. т. площадей и линий очень просто определяются на основании двух теорем Паппа (Гульдена). 1) Если плоская линия вращается вокруг оси, лежащей в плоскости этой линии, но не пересекающей ее, то образующаяся поверхность численно равна произведению длины вращающейся линии на длину пути, описанного Ц. т. этой линии. 2) Если плоская фигура вращается вокруг оси, лежащей в ее плоскости, но этой фигуры не пересекающей, то объём получающегося тела вращения численно равен произве-т дению площади вращающейся фигуры на длину пути, описанного ее Ц. т. Приложим последнюю теорему к нахождению Ц. т. полукруга. Если полукруг вращается около своего диаметра, то
^ πα3=2 пу · ^ πα2,
откуда
У =
3πα3
π2α2
4 а 3 π
Применение веревочного многоугольника к определению Ц.т. площадей. Разбивают площадь мн-ка (фигура 4)
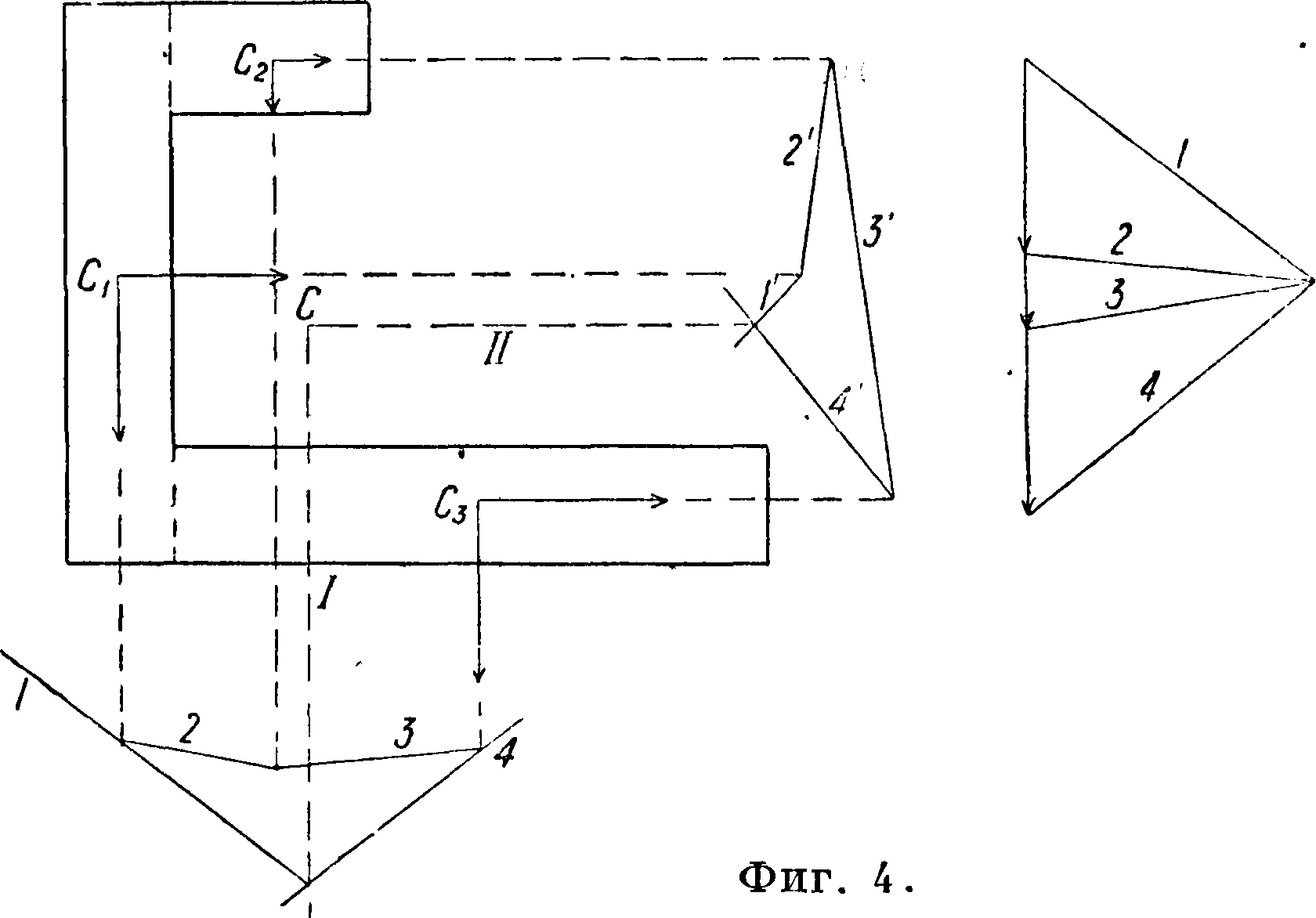
на части, положение Ц. т. которых известно, и прикладывают в Ц. т. вертикальные силы, пропорциональные площадям. Построив веревочный мн-к, продолжают крайние стороны его и через точку Пересечения их проводят прямую I, параллельную силам; она и будет линией действия равнодействующей. Повернув силы вокруг точек их приложения на нек-рый угол, строят снова линию действия II равнодействующей. Искомый Ц. т. находится в точке пересечения С обеих линий действия равнодействующей. Если мн-к имеет ось симметрии, построение второго веревочного мн-ка излишне. На фигуре 4 силы повернуты вокруг С19 С2 и С3на 90°, и потому веревочный мн-к 1,29 34
Название фигуры
Вид фигуры
Координаты Ц. т. фигуры
Периметр треугольника АВС а+Ь+с=2р
Дуга ADB круга
, г“а·л ЛI— ———=0,0349 га У о
Линии
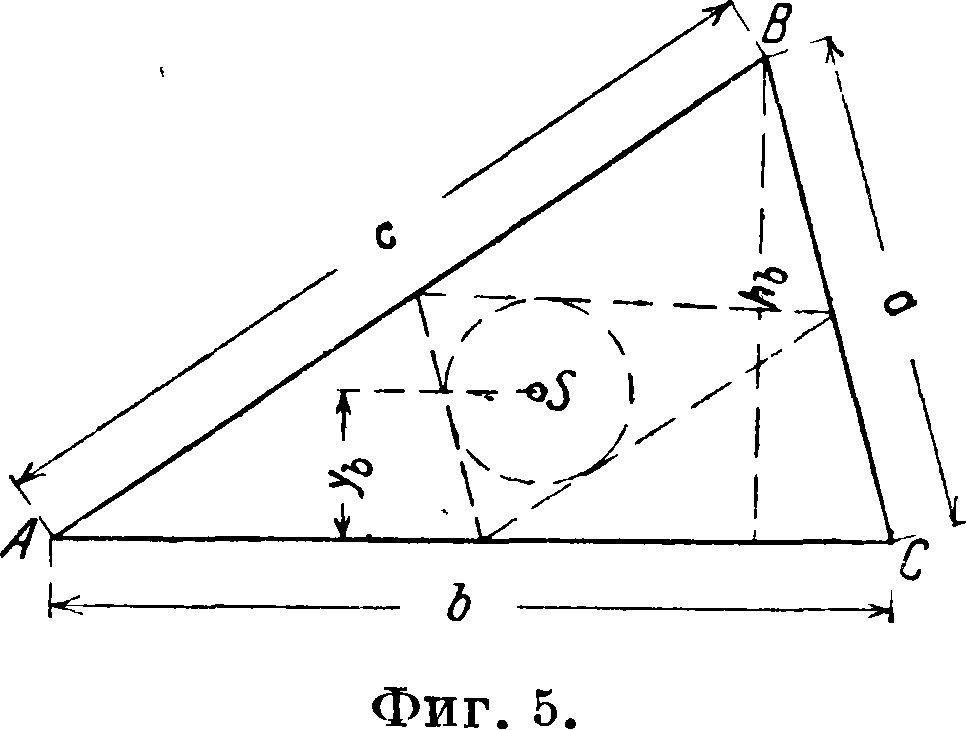
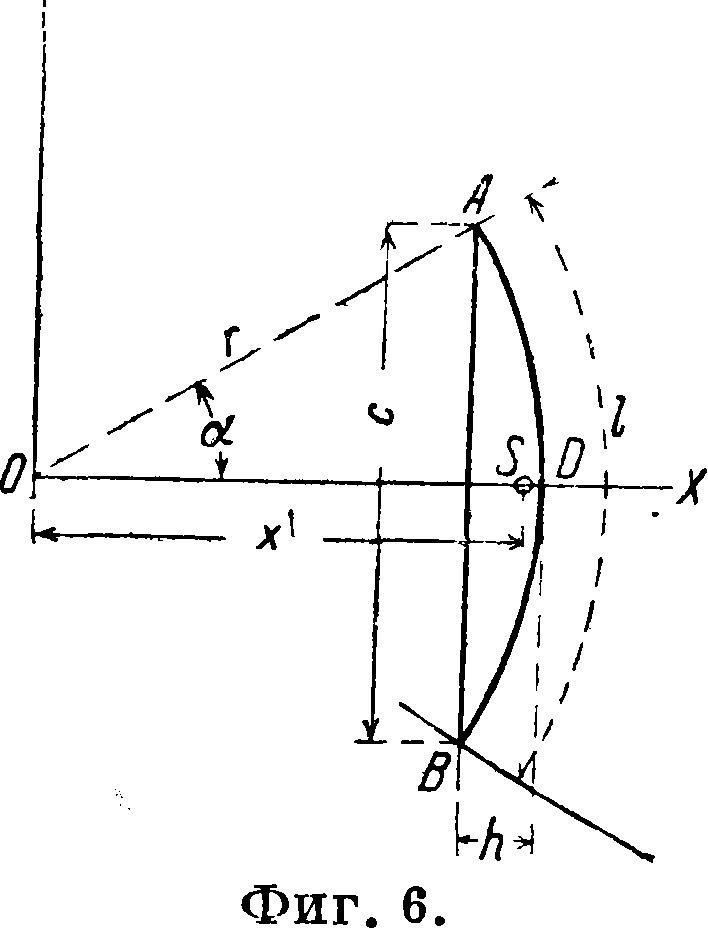
Ц. т. в центре круга, вписанного в тр-к, вершины которого лежат на серединах сторон данного тр-ка:
1. а + с
УЬ=Ткъ-^+ь—с г-с c(c2 + 4h2) ^ sina
= Т"= Ш ~ г * ” *
Для полуокружности
t=— п я=— ^0,6365г;
2 π
ДЛЯ окружности ггУг
X — -
-=0,9003г;
для произвольных плоских дуг
-4
Часть периметра правильного мн-ка ABCDE
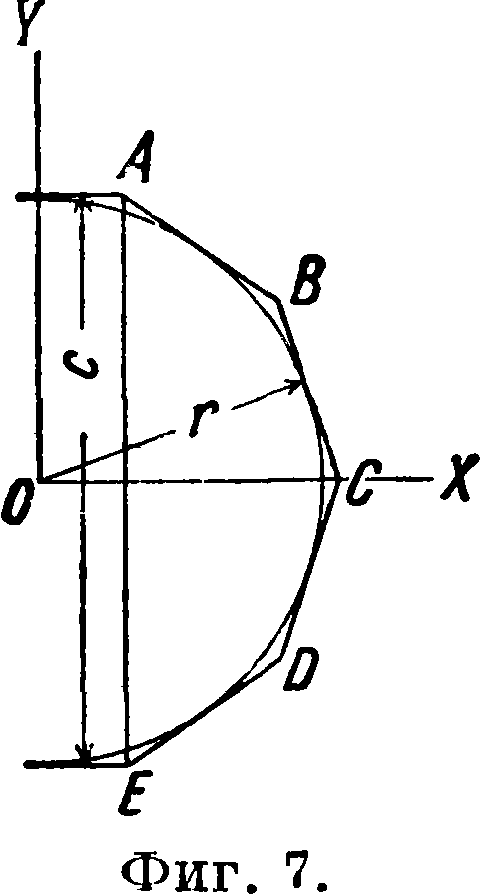
L г
где г—радиус вписанного круга, L—длина ломаной линии ABCDE
Площади
TP-к АВС
Ыг Ь л Г _ /а2 + Ь2-с2 2
-Ύ-tV а {-15--) :
s — Ур(р-а)(р-b)(р-с)
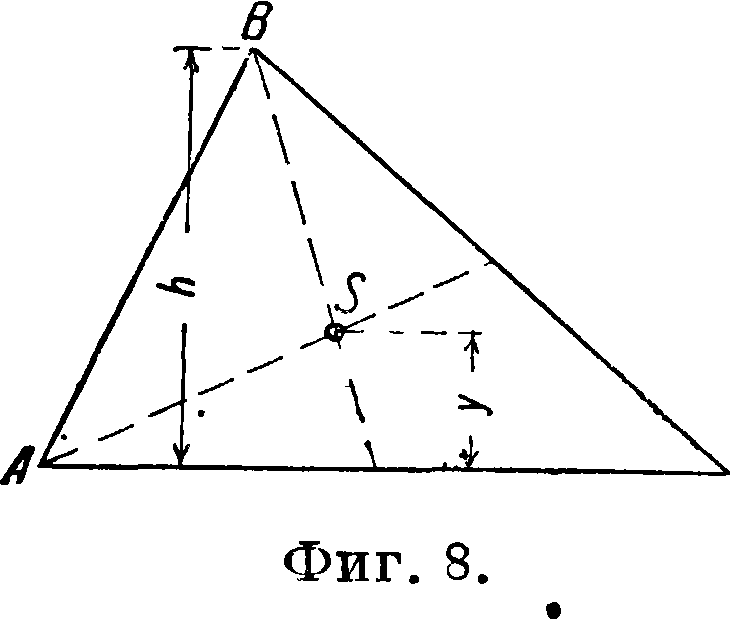
h
Ц. т. лежит на линии, соединяющей вершину с серединой противоположной стороны, на Ч3 высоты, считая от основания. Координаты S составляют среднее арифметическое координат вершин тр-ка, например
- Х1+Х2+Х3
X- 3
Трапеция ABCD (a- -b)h
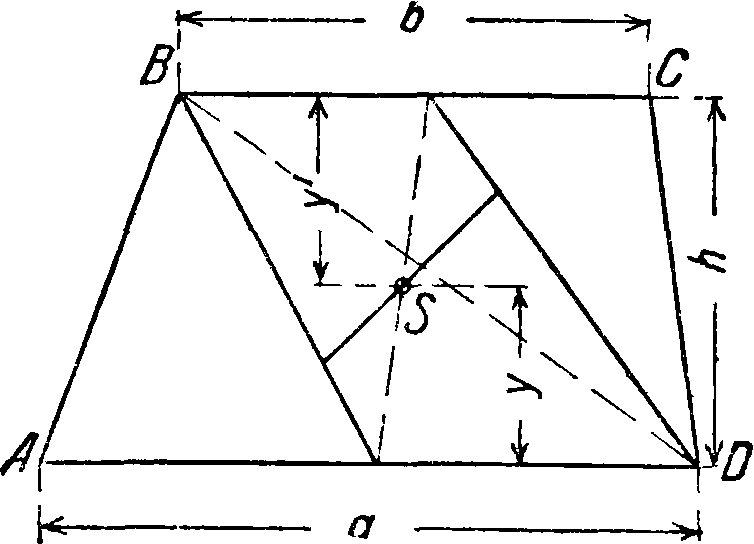
У=V -
h cl -j- 2b
з cl -f- b
h 2a + b 3 a 4“ b
‘ Фигура 9.
Название фигуры
Вид фигуры
Координаты Ц. т. фигуры
Круговой сектор OADB S=-i- т1=0,01745 аг2 (смотрите фигура 6)
Фигура 10.
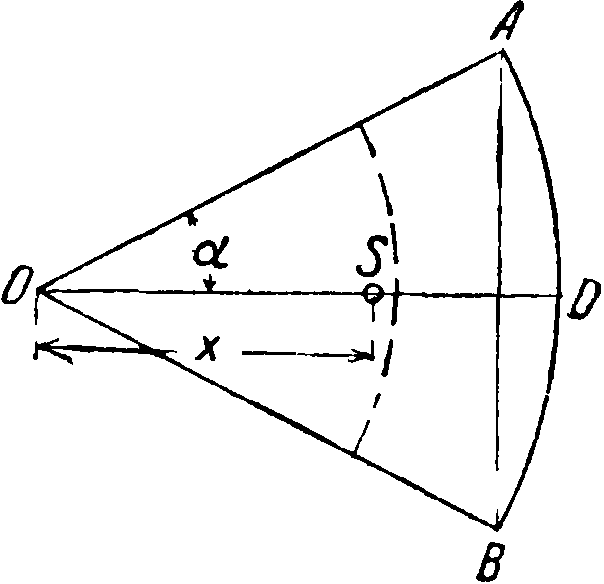
Круговой сегмент ADB *=i[rl-c(r-h)]
См. фигура 6.
Часть кругового кольца АВЕС
δ=π(Κ2-τ·2)
Фигура 11·.
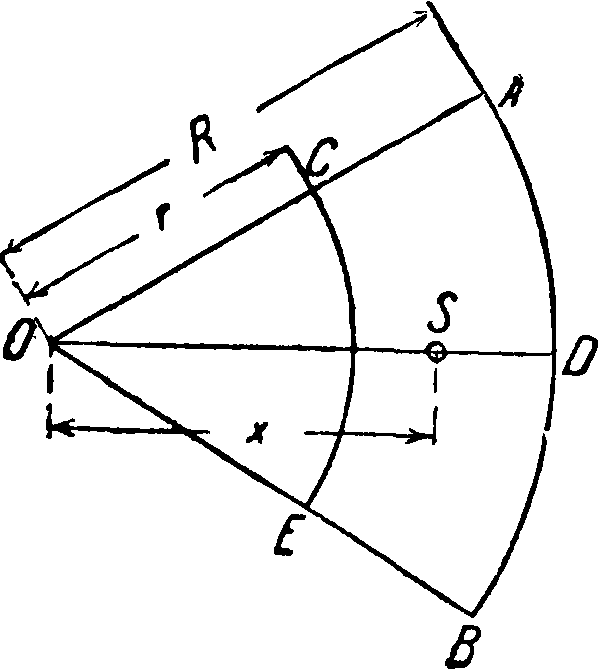
- 2 Sin а х=-^г·.--
о а
Для полукруга
— 4 г х=—^0,4244 г;
ол для четверти круга
— iV 2 · г я == _-^0,6002 г
- с3 2 г3 sin3 а X~l2s~T s *
~ = 2_ ^ Sin3 а
В α-sin a COS а
— _ 2 R3 — г3 sin а Х “ 3“ ‘ Я2_г2·α
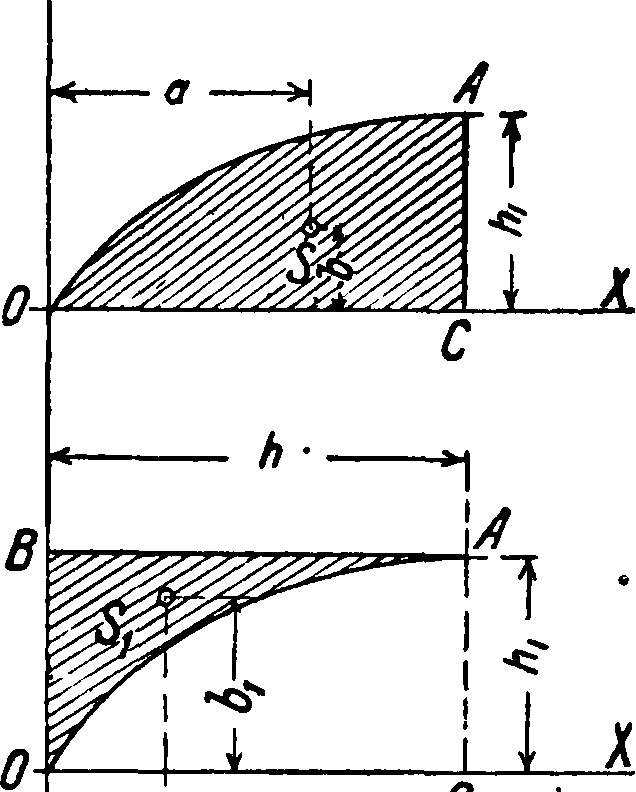
Парабола
s = Yxy
Фигура 12. u
Поверхности
Боковая поверхность прямой призмы 2 p-h
(2р—периметр основания)
| ;г-- | |С 1 | 1 |
| 1
1 |
Г 1
1 • 1 N | |
| i— |
Фигура 1В.
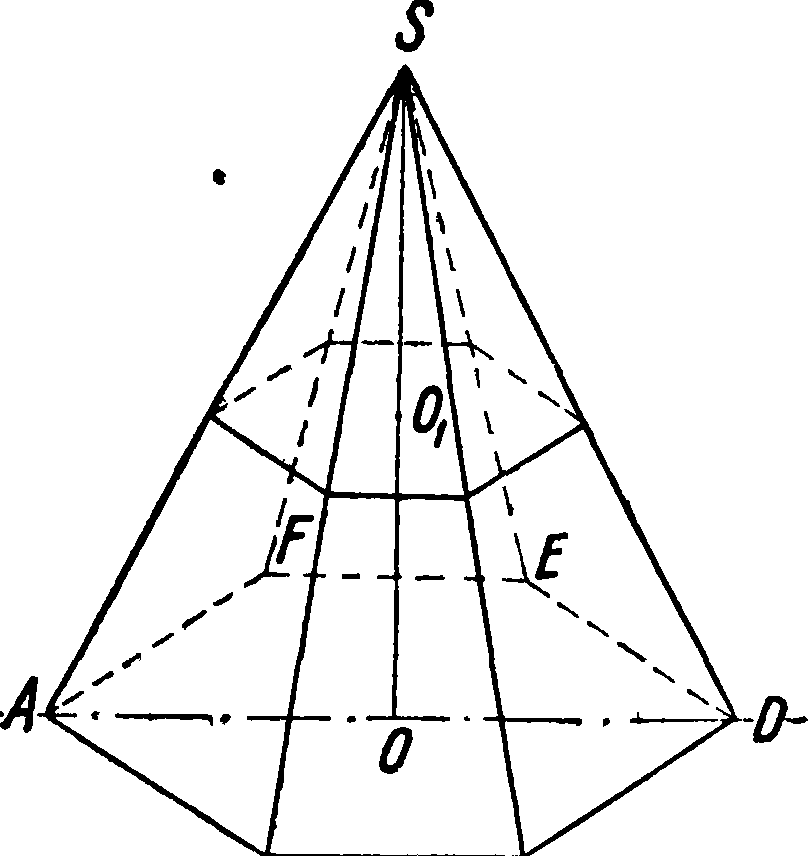
Боковая поверхность правильной пирамиды и прямого .кругового конуса
snup. — Phi
(р—полупериметр основания; hi— апофема пирамиды);
skoh. — nrI (i—образующая)
3 h, Sh! а — —. b ——:
5 ’ 8 ’
<4=0,2/ι, bг=0,75/1!
Ц. т. совпадает с Ц. т. периметра среднего перпендикулярного сечения
В С
Фигура 14.
Ц. т. совпадает с Ц. т. периметра сечения, проведенного перпендикулярно к высоте, на расстоянии i/3высоты, считая от основания
Название фигуры
Усеченная пирамида и усеченный конус
V=—(£ +6+/£Ь);
V =у-я(й2 + 7‘2 + Дг)
Вид фигуры
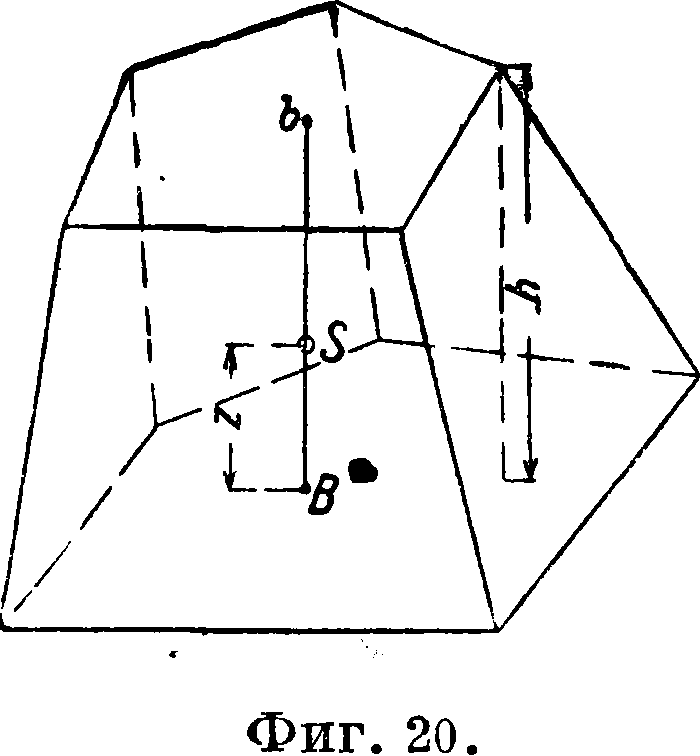
Координаты Ц. ϊ. фигуры
z = h(B + 2VBb+3b) #
цв+УШ+b)
h(R* + 2Rr + 3r)
4(Й2 _|_Rr~ ~r2)
Ц. т. — на прямой, соединяющей. Ц. т. оснований
Шаровой сектор
У=— лг“К=2,09Ur*h 3
См. фигура 10 и 15.
y=~(l + COs a)r=~(2r~h).
Для полушара 3
у=—г У 8
Шаровой сегмент V=*v(r-±)
л I*
= 61У ’
где I=АС,
См. фигура 15.
У =
Vi=DS =
3(2r-h)2 ЦЗг-h) *
h(ir-h)
4(3r— h)
Для полушара у=уг=— г
Полый полушар -|я(й3-г·3)
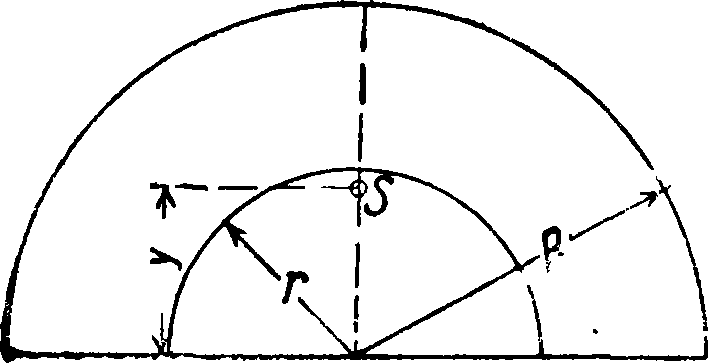
3 R*-r* 8 * R*-r*
Фигура 21.
V =
Клин (2a + c)bh
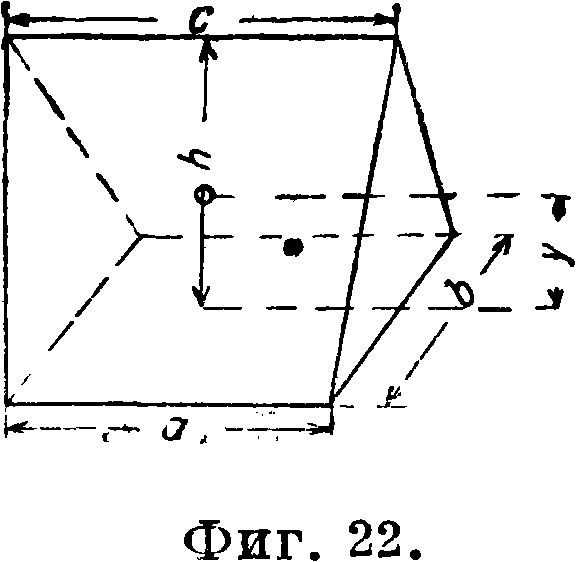
У =
h (а + с) 2(2а + с)·
Ц. т. — на прямой, соединяющей Ц. т. основания с серединой острия клина

х =
построен непосредственно (без построения нового мн-ка сил), т. к. стороны его должен быть перпендикулярны к соответствующим лучам мн-ка сил 1, 2, 3, 4.
Выше в таблице приведены координаты Ц. т. наиболее часто встречающихся фигур.
Лит.: см. Механика теоретическая. В. Никаноров.