Центроида

Центроида, полой да, геометрии, место мгновенных центров (полюсов) скоростей при всяком непоступетельном движении плоской фигуры. Мгновенным центром вращения для данного положения отрезка, движущегося в плоскости, является точка пересечения нормалей к траекториям, описываемым концами отрезка. Мгновенный центр, меняя свсе положение, образует траекторию как в неподвижной, так и в движущейся плоскости. Геометрии, место мгновенных центров на неподвижной плоскости называется неподвижной Ц. (по-лоидой), на самой фигуре—подвижной Ц. По теореме Пуансо непрерывное движение плоской фигуры в ее плоскости м. б. получено, если, построив две Ц. и соединив одну из них неизменяемо с плоской фигурой, катить без скольжения первую Ц. по второй (неподвижной). Меняя роли Ц., то есть делая подвижную Ц. неподвижной и неподвижную подвижной, получают движение, называемое обращенным по отношению к первоначальному (гм. Аксоиды. Мехатта теопетичр.ская). При каждом повороте подвижной системы одна определенная точка ее совпадает с полюсом, лежащим в неподвижной плоскости. Точка эта называется подвижным полюсом или подвижным центром вращения.

С понятием Ц. связан ряд вопросов прикладной кинематики (профилирование зубчатых колес, выбор очертаний в механизме катящихся рычагов и прочие). Изучение Ц. позволяет глубже исследовать движение: нередко выясняется, что движения, производимые совер

шенно различными с внешней стороны способами, оказываются кинематически вполне эквивалентными; выясняется смысл обращенного движения механизма и прочие (смотрите Механика прикладная). Пример. Рассмотрим механизм антипараллелограма (частный случай двухкривошипного механизме), противолежащие звенья которого АВ— СВ=2а; ВС~=АВ=2с (фигура 1), причем а>с. В плоском дви

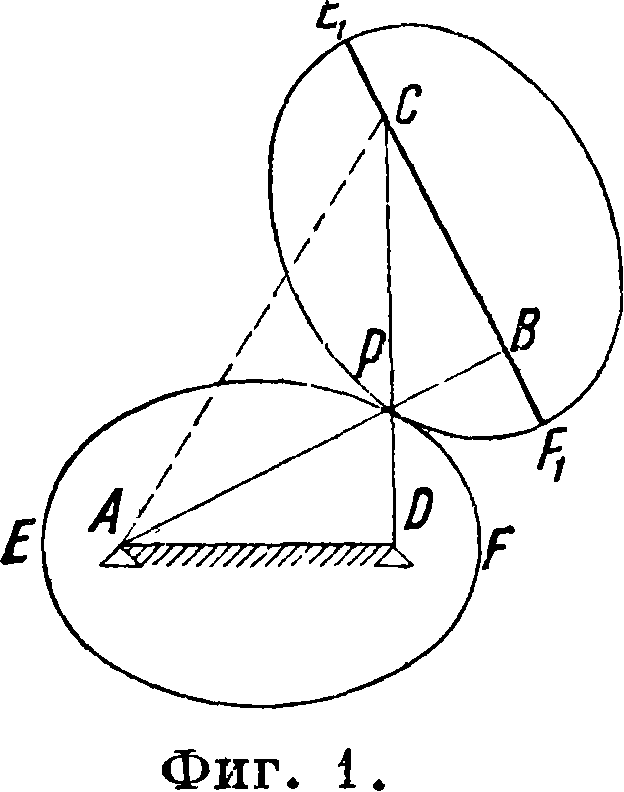
жении, совершаемом звеном ВС относительно звена АВ, называемого стойкой, траектории ртю точек В и С — окружности радиусов^.# и

ВС. Мгновенный центр лежит на пересечении нормалей к этим окружностям (или перпендикуляров к скоростям точек В и С), е. в точке Р. Из равенства тр-ков АВС и АВС следует, что /_АВС= /_АВС; т. о. ААРВ=АСРВ, откуда АР=РС; ВР=РВ и потому АР -f ВР=АР + РВ=2а.

Точно так же

СР + РВ=СР + РВ=2а.

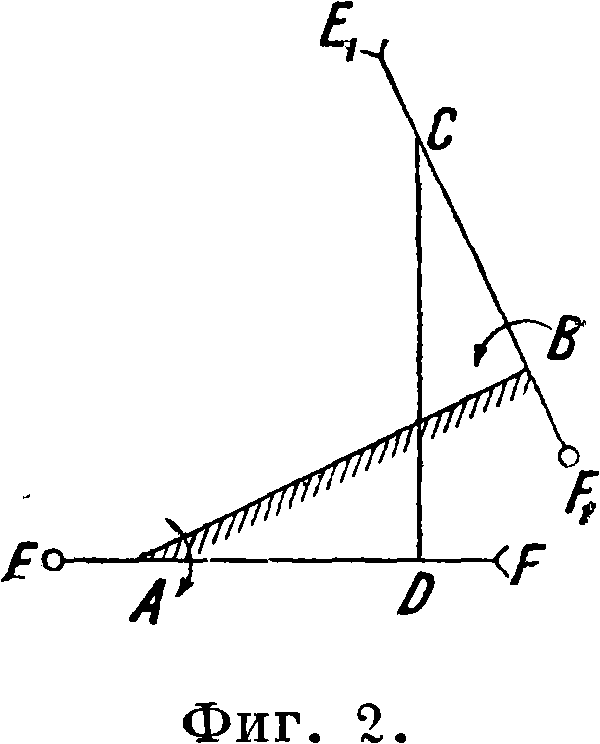
Итак, сумма расстояний мгновенного центра Р от двух неподвижных точек Ап В есть величина постоянная. Неподвижная Ц.—эллипс с фокусами в точках-И и В. с большой полуосью а и малой полуосью Ь=]/а^а — с^а · Аналогично подвижная Ц.—также эллипс с полуосями той же величины и с фокусами С и В. Т. о. движение, при котором второй эллине катится без скольжения по неподвижному эллипсу, кинематически эквивалентно движению звена ВС антипапяллелогоама относительно звена АВ. Движение этих звеньев друг относительно друга м. б. осуществлено например при помощи двух эллиптических зубчатых колес EFnE^x, из которых первое будет вращаться около оси, проходящей через фокус А, а второе—около оси, проходящей через фокус В. Подобным образом если закрепить звено А В и освсбодить звена А В (фигура 2). то движение звена СВ (противоположного стойке) будет кинематически эквивалентно движению двух Ц., представляющих собою гиперболы. В. Никаноров.

Лит.: см. Механика прикладная и Механика теорет-тическая.