Цепная линия

Цепная линия, трансцендентная кривая, форму которой принимает упругая нерастяжимая нить, подвешенная в двух точках и не сущая равномерно распределенную по длине нагрузку. Ур-ие Ц. л.:

X X

р^а - - е ее

У=? ( е^а + e ^a)=ach-,

^ OL

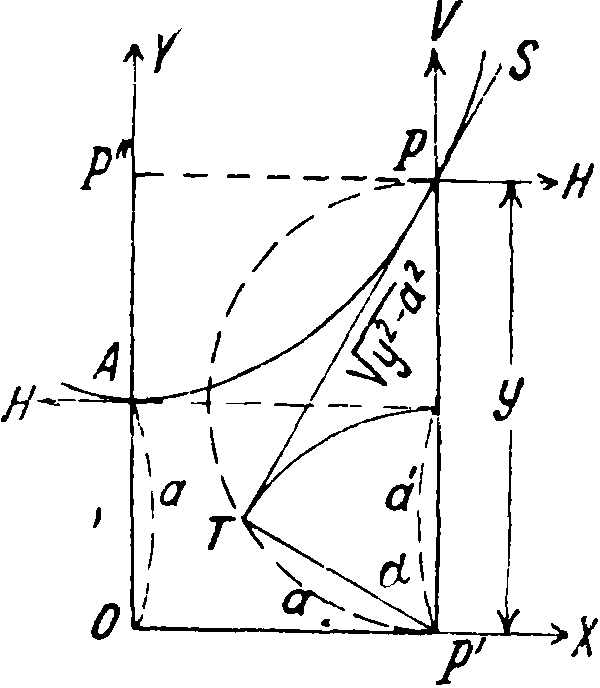
откуда видно, что Ц. л. симметрична по отношению к оси у-ов; ее вершина (низшая точка) имеет ординату а (фигура).

Уравнение касательной в точке Р»(Хо, 2/р)·· _

УД-«²_

У —У о

X-Xq

= tga =

dy dx ‘ *e

(*o _ ^xe

e ^a - e ^a ) =

Построение касательной. Строят на jРР полуокружность, откладывают от P хорду РТ, равную а; РТ—касательная (Т— точка эвольвенты Ц. л.).

Радиус кривизны (равен нормали цепной линии)

_ρ=Α

^с а

Длина дуги:

a sh - ·-- У у² - а²=РТ

Площадь ΟΛΡΡ (пропорциональна длине дуги АР)

F-

х х V

Да² ( е“ - ) =

= а · У у²— а²=2 Δ РРТ=а <

Параметрические уравнения. Если ввести в качестве параметра угол а наклона касательной к оси ж-ов, то предыдущие ур-ия примут вид:

а. · а у. х=аArsh(tga), у=-

COS²a COS a

tga=sh^; F=a² tga; s=a-tga.

Построение Ц. л. 1) Параметр а дан; наносят линию с помощью таблиц гиперболич. ф-ий. 2) Даны длина 2 L Ц. л. и расстояние 21 между двумя симметричными точками; на основании предыдущего

L=atga; х — I=а Ar sh (tg a)

и если tg a=sh v, то

L_ _ sh v

l ~ v

Из таблиц подбирают соответствующее значение v и отсюда tga и а. Тогда:

L L I. _ L

“ tg a Sh V V ’ У sin a

распо-

то

Есл и даны расстояние 21 симметрично ложенных точек и стрелка провеса f,

х=I=a Ar sh (tg a)=αν, γ=;

ΐ=·£^-α=α₍ΥΤ+Ί^-ί) =

= а (У 1 -f sh² v — 1)=a (ch v — 1); v, как и выше, определяют из таблиц; отсюда

I _{т 7} sh V

а — -, L=l---

V ⁷ V

Ц. л. как веревочная кривая—см. Веревочный многоугольник.

Если нагрузка равномерно распределена не по пролету, а по длине цепи (собственный вес и тому подобное.) и величина-нагрузки на единицу длины составляет # кг/м, то натяжение 8 в произ-

вольной точке цепи, горизонтальная и вертикальная составляющие его Н и V выразятся:

Я=q. α= q У у^г — s²; V=q · s: S=q · у,

где s—длина дуги Ц. л. (фигура); следовательно я параметр α= —.

Теория Ц. л. применяется при расчете силы натяжения и величины провеса в случае упругих опор (разгрузочные и угловые мачты воздушных проводов для сильных токов; висячие мосты и прочие). Коэф. а зависит от силы натяжения и от веса провода. В известных случаях (например подвесные дороги) он настолько велик, что дробь ^ мала и при очень больших значениях х. В этих случаях очень выгодно, разложив показательные ф-ии в ряд, взять только несколько первых членов ряда. Т. о. (смотрите Дифференциальное исчисление):

е а х х^{2 хг}, а 2 а^{2 1} 6 а³

а _ i _ ^х i ^χ2. а ~ 2 а²

х³6 а³

и ур-ие Ц. л. примет вид:

.×Хк

!=;(«“ + е~^а) =

Я²

к а х“

Для малых значений ^ наиболее простой формой Ц. л. является то есть парабола (известно, что Галилей отождествлял Ц. л. с параболой).

Пример. Определить форму провода, если расстояние между его опорами 80 метров и длина стрелки 1 м.—Перенеся начало координат в низшую точку провода," получаем уравнение провода в виде

χ²

У=2Ϊ-

Т. к. у=1 метров при х=40 м, то. 1=~ и α= 800, следовательно ур-ие провода будет:

_ х²

У ~ 1 600*

Ур-ие же Ц. л. при тех же условиях имеет вид

γ2 χ4 хб

У =—__I_____I______L

^у 2 - 800 ^п 24 · 800³ ~ 720 · 800⁵ ~

Разница между ординатами обеих кривых

2478003*

720^8005

В виду быстрого убывания членов ряда она м. б. принята равной приблизительно первому члену

404 _ 40 40 ³ 5 5

24 - 800^{3 —} 41 830 J ^— 24 000 ^М ~ 24 ^MM

Цепная линия может характеризовать функцию изменения расчетной нагрузки арочных мостов в зависимости от формы свода. См. Кривые, Металлические мосты, Висячие мосты, Транспорт подвесной, Гиперболические функции. в Никаноров.