Циркуляция

Циркуляция, интеграл по замкнутому контуру от скалярного произведения векторного поля на диференциал дуги контура. Ц. обозначают символом «Г»:

Г=j)Fdb=j)F · dr =(j) (X dx + Ydy + Zdz). ОС с

Здесь символ ф означает интеграл по замкну тому контуру С; F=iX + jY -f kZ — вектор, имеющий в каждой точке пространства (поля) свое определенное значение; i_t j и k — орты по осям координат (смотрите Векторный анализ); iX, /У, kZ — компоненты вектора F; dr=idx + -±jdy + kdz — диференциал радиуса вектора г, описывающего рассматриваемый контур; dS — элемент дуги контура как вектор или элемент касательной к контуру; х> у, г — координаты соответствующей точки контура. Выражение ь

А=JFdS=j {Xdx+Ydy + Zdz)

a a

μ. б. названо течением вектора F по контуру δ от точки а до b. В частном случае, когда вектор есть сила, выражение А представляет собой работу силы F на пути δ от а до 6. Течение, или работа, по замкнутому контуру есть Ц. Если векторное поле F имеет потенциал F== grad φили

γ — ^д<р V=^д<р 7 —

^Λ dx’ ду * dz ’

где φ — потенциальная ф-ия, то течение, или работа, вектора выразится так:

А=j FdS=J grad φ. dS =

a a

= f d<P=<Pt — Ψα> a

t. e. будет равна разности потенциалов для конечной и начальной точек. Ц. по замкнутому контуру для потенциального поля равна нулю:

= (j)grad

G с ибо в этом случае q>_b

φ · dS=щ — φ_α=0,=<Ρα·

При рассмотрении вопросов, связанных с Ц. по контуру в векторном поле, большое значение имеет связь Ц. с потоком вихря поля через поверхность, ограниченную данным замкнутым контуром. Эта связь дается теоремой Стокса

V · db

J*J* rot V · dS=2 ^ύ S

Я- ·^ds

и гласит: Ц. вектора v по замкнутому контужу С равна потоку вихрей этого вектора, пронизывающих произвольную поверхность S, ограниченную контуром С. Доказывается эта теорема непосредственным вычислением Ц. по замкнутому контуру. Возьмем элементарный контур АВС, построенный близ произвольной точки N_t взятой в поле вектора v_t в форме периметра наклонной грани тетраэдра, ребрами которого являются приращения координат в поле вектора v (фигура 1). Если v_xi v_y и v_z — компоненты век-

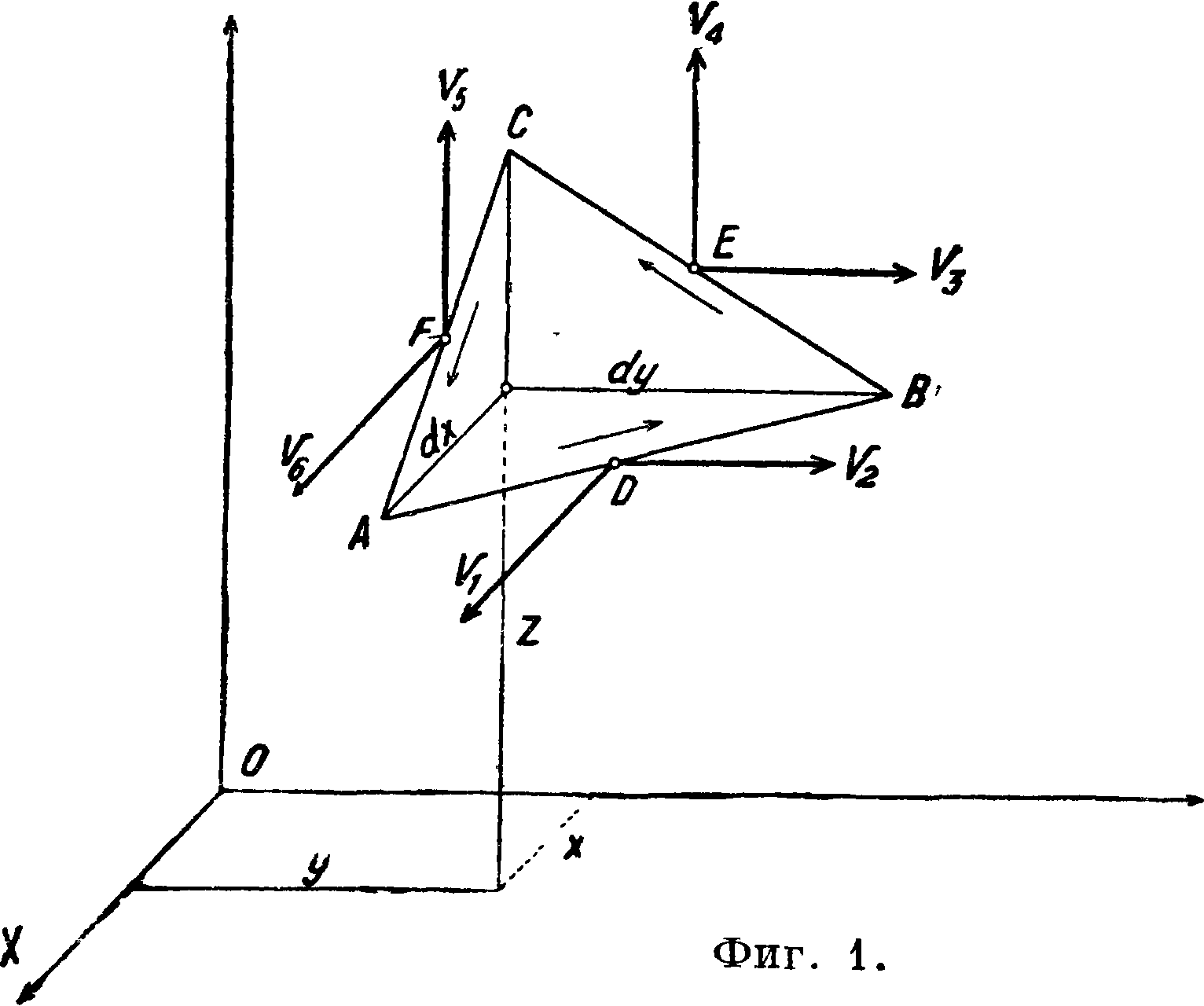
тора в точке iV, то с точностью до бесконечно малых первого порядка значения вектора v, имея в виду элементарно малую область NABC, в точках .D, Е и F будут следующие:

г₄:

^Vb ^:

= ^v* ΊΓ

*₊t

-ν_χ+γ

^t^dz+ τ

4^ + 4

dv_z

dvx

Элементарная Ц· по контуру ABC вычисляется так:

άΓ=[v_b — v_t) dx -f (v₂ — v₃) dy -f- (v₄ — v₅) dz =

- + τΗ5--^Η·"" +

- %) - [( W -1») ^cos ° +

+(t—%)·»/> + №-

— -") ^cos у] ^dlS=2 (ia>_x -¥j(o_y + kw_z). dS== rot v · dS;

здесь α, β и у—углы, составляемые нормалью к площади АВС с осями координат; dS — площадь Δ АВС; ω=ίω_χ + jco_y -f угловая скорость вращения частицы жидкой материи в точке А, если векторное поле v есть поле скоростей.

. ± (дУ_т __

2 дг

dv_z	— ^dvy	1.	СО s=
ду	dz _t	г	^wy
-V	=	1	-
г		2	V дх
L V	в токе	А	есть:

>я“ · "·

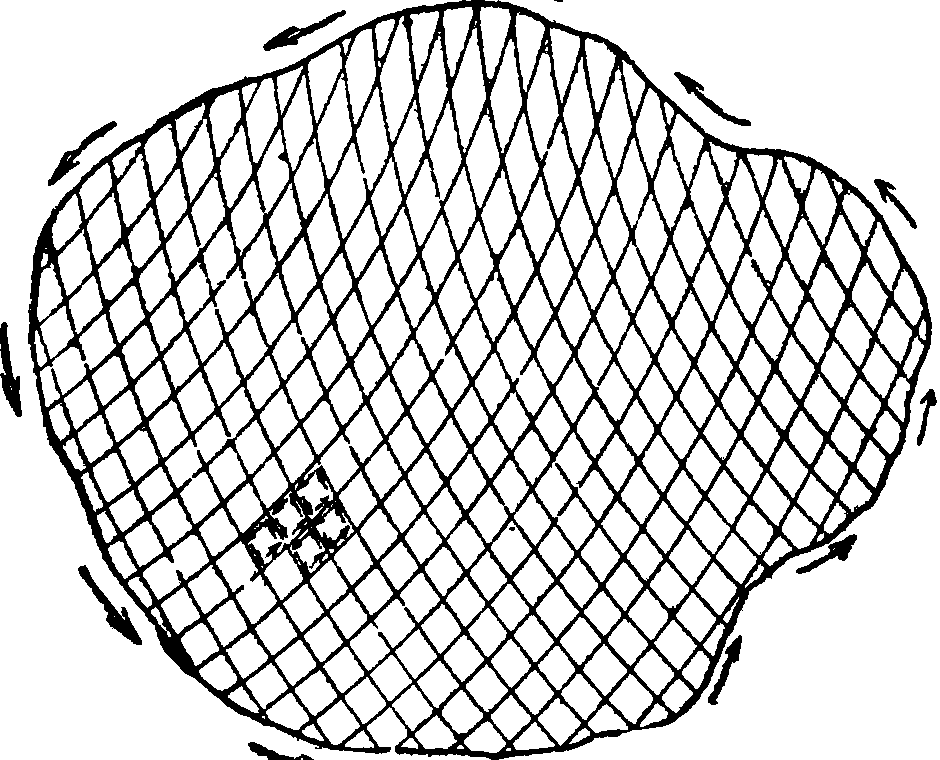
Вычисляя Ц. для произвольного конечного контура С, получим таковую суммированием по элементарным контурам, которые можно провести на поверхности S (фигура 2):

Г=(j) vdb=(j) [v_x dx 4- v_y dy + v_z dz)=о 0

~ j Jrotv. dS>

s s

Теорема Стокса позволяет преобразовывать интеграл по кривой в поверхностный интеграл.

Если рассматри-ваемое векторное поле есть поле скоростей внутри жидкости, сплошь заполняющей пространство и перемещающейся в нем, то понятие Ц. имеет особое значение для исследования движения жидкости. Здесь наряду Фигура 2. с теоремой Стокса имеет значение теорема Томсона, а также ряд теорем Гельмгольца, касающихся вихревого поля, имеющего место в поле скоростей, и составляющих основу вихревой теории (смотрите Вихревая теория).Теорема Томсона говорит, что движение совершенной жидкости, бывшее в некоторое мгновение времени безвихревым, остается и в дальнейшем безвихревым, если на частицы жидкости действуют те же объёмные силы, что и в первоначальный момент времени, и притом имеющие потенциал. Рассматривая изменение Ц. по некоторой кривой, проведенной внутри жидкости, в зависимости от времени имеем:

d dt

V · db

о Ь

db + V

<§4г№ ^s) =

(Λ)].

Согласно ур-ию Эйлера (смотрите Гидродинамика) у.grad p-K-«L,

где К=iX Λ-jY - -kZ — ускорение действующей объёмной силы; ρ — плотность жидкости;

р — гидромеханич. давление; --действитель ное ускорение движения материальной жидкой частицы. Т. к. объёмная сила имеет потенциал, то К *= grad Е7, где U — потенциальная ф-ия;

J?P_ JL i ^дР дх dy

t^L 4- ; <*LjLb ^дидх J ду dz

(пенятие о градиенте — см. Векторный анализ).

grad р=grad U :

Имеем:

· db=К · db — -i- grad ρ · db =

= grad U · db —i- grad ρ · db. Выражение

Έ W-d{£)=dv. ·

Тогда для изменения Ц. :.*меем

(_ν db)=grad U · db — ~ grad ρ · db -f v dv. Интегрируя, получаем

= (j) grad Udb — ^ i- grad p · dS +

т. к. grad pdb =dp и grad U db=dU. Выражение, стоящее в правой части ур-ия, для замкнутой кривой равно нулю; значит

1й фгм“8=0

или при наличии силового потенциала Ц. по любому замкнутому контуру с течением времени не изменяется; это и есть выражение теоремы Томсона. Исследование лобового сопротивления дви жения жидкости в каналах и трубах и другие важные вопросы гидродинамики получают более четкое освещение при помощи понятия о Ц. скорости

Лит.: Фиников С., Векторный анализ, 2 изд. М.—Л., 1932; Александров В., Техническая гид, родинамика, М., 1932; Forchheimer Ph., Hyd-raulik, В., 1930; Kaufmann W., Angewandte Hydro-mechanik, B., 1931; Prandtl L. u. Tietjens O-Hydro- und Aeromechanik, В. 1, B., 1929, B. 2, B., 1931;Pr4sil F., Technische Hydrodynamik, 2 Aufl., Berlin, 1926; Lamb H., Lehrbuch d. Hydrodynamik, Berlin, 1931. В. Брилинг.