> Техника, страница 92 > Шарнирные направляющие механизмы

Шарнирные направляющие механизмы

Шарнирные направляющие механизмы, механизмы, отдельные точки звеньев которых описывают траектории, являющиеся пря мыми или весьма близкими к прямым, без устройства специальной поступательной пары для обеспечения этого движения. Ш. н. м. делятся на две группы: первая—точные направляющие механизмы, то есть такие механизмы, у которых траекториями являются точные прямые, и вторая—приближенные направляющие механизмы, у которых траектории близки к прямым.

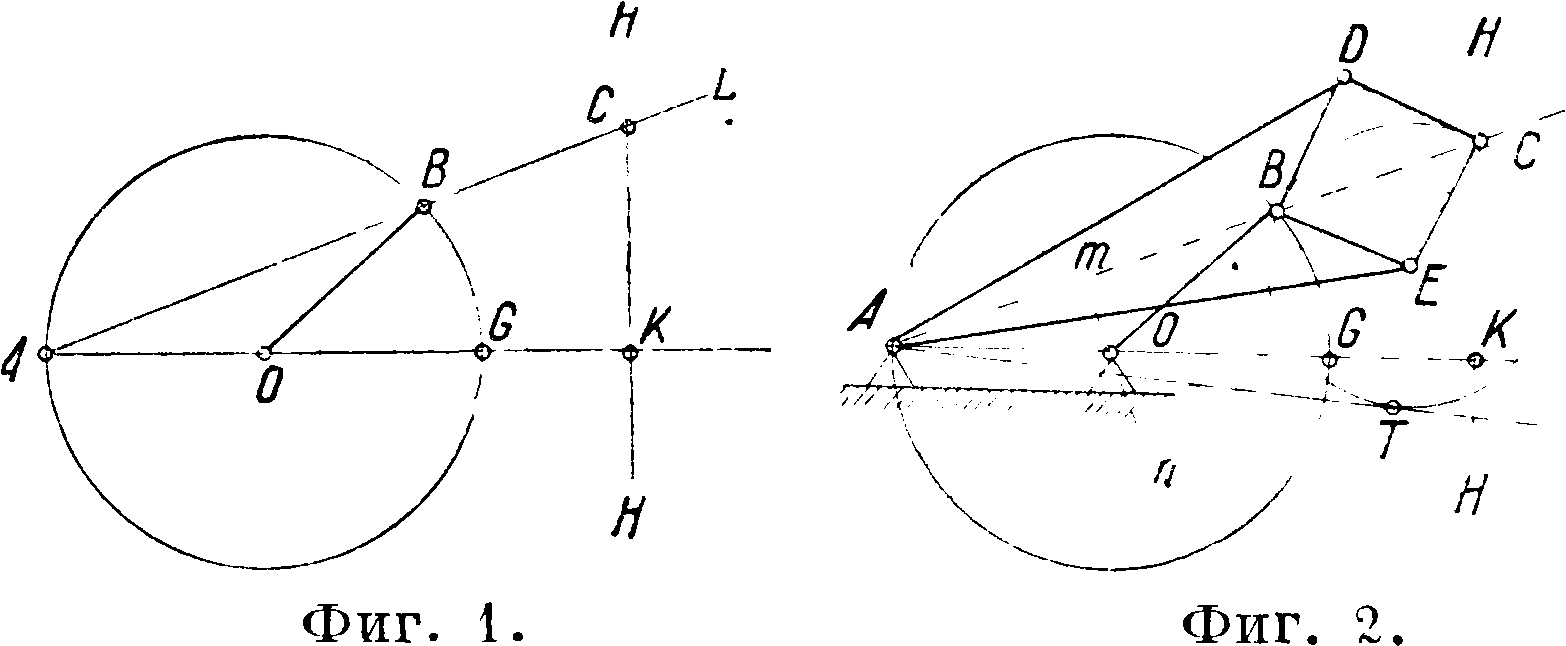
Первая группа III. н. м. весьма невелика и основана гл. обр. на использовании нек-рых геометрии. соотношений. Вторая группа Ш. н. м. бесконечно велика, т. к. в каждом механизме имеются точки, движущиеся по траекториям, б. или м. близко подходящим к прямой линии. Из точных Ш. н. м. необходимо отметить механизмы, построенные на использовании геометрии. свойства, называемого инверсией (смотрите Инверсия в математике), откуда вся группа этих механизмов получила свое название и н-версоров. Уравнение инверсий, используемое для построения механизмов, относится к случаю, изображенному на фигуре 1, когда одна

из окружностей обращается в прямую НН и удовлетворяется соотношением:

AB-AC=AG-AK=K².

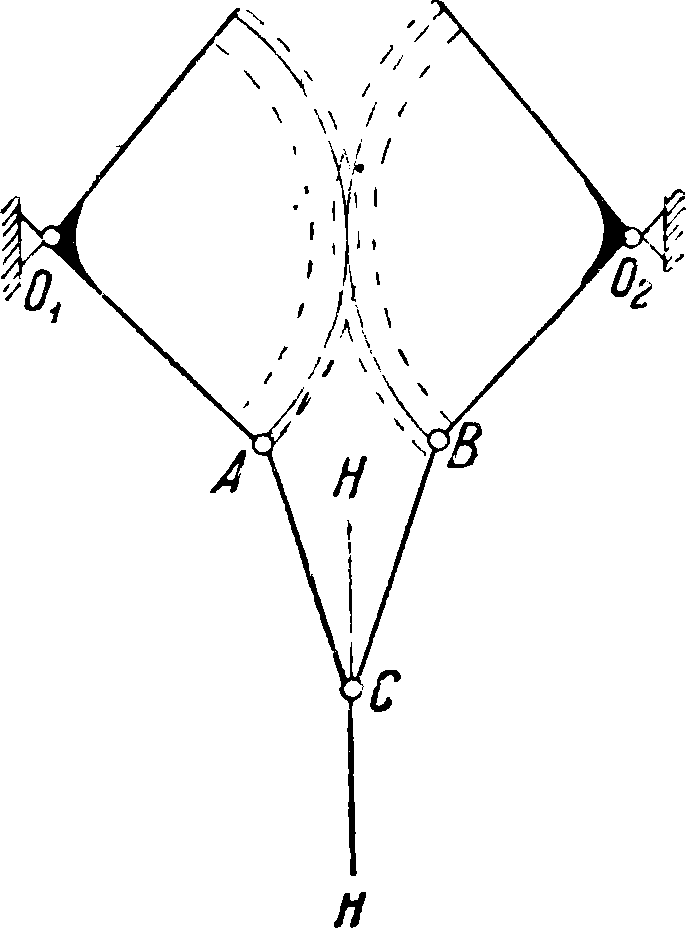
Прямая НН (фигура 1) и использована в механизме положительного инверсора Поселье-Липки-на (фигура 2), предложенного франц. инж. По-селье в 1864 г. и независимо от него русским ученым Липкиным в 1871 г. Этот механизм должен удовлетворять условию:

AD=АЕ BD=OC=EC=BE и АО=ВО.

При этих условиях точка С будет описывать прямую, перпендикулярную к 40. В самом деле, точка С всегда лежит на одной прямой с В и А, т. к. по свойству ромба диагональ ВС делит отрезок ΏΕ пополам и к нему перпендикулярна; высота равнобедренного тр-ка АНЕ делит DE пополам и к нему перпендикулярна. Следовательно диагональ СВ совпадает с высотой и значит проходит через точку А. Из точки Е опишем окружность радиусом ЕС, которая вследствие равенства ВЕ=ЕС пройдет через точку В. Проводим из точки А касательную АТ к описанной окружности. Тогда имеем:

АВ · АС=АТ² ----- Const,

т. к. радиус ЕС остается все время постоянным, а центр 12 находится на постоянном расстоянии

АЕ от точки А. При движении точки В по окружности, проходящей через точку А, центр этой окружности О будет лежать на перпенди-

В V

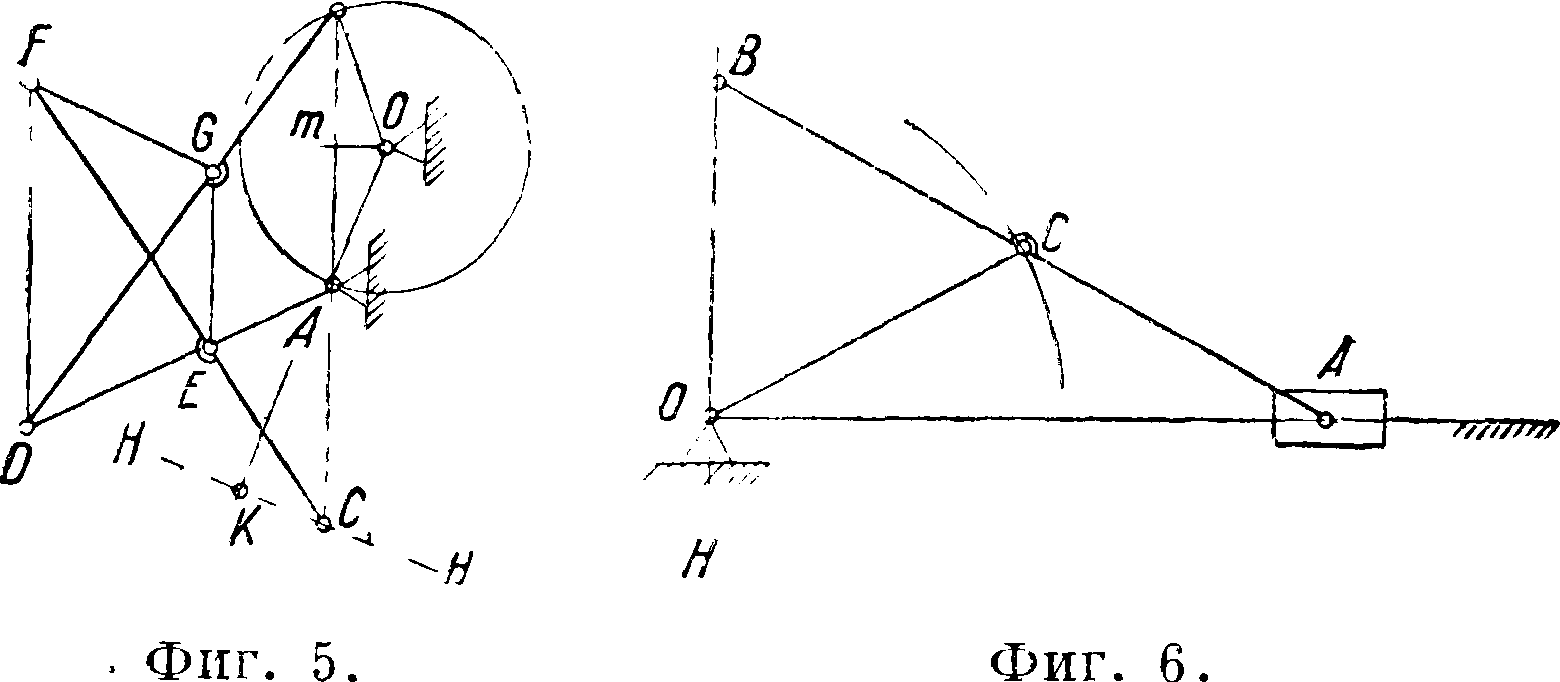
куляре тп, восстановленном "из середины отрезка АВ. Соединяя точку В. с точкой О с помощью звена ВО, получим при движении всего механизма AECDBO перемещение точки С по

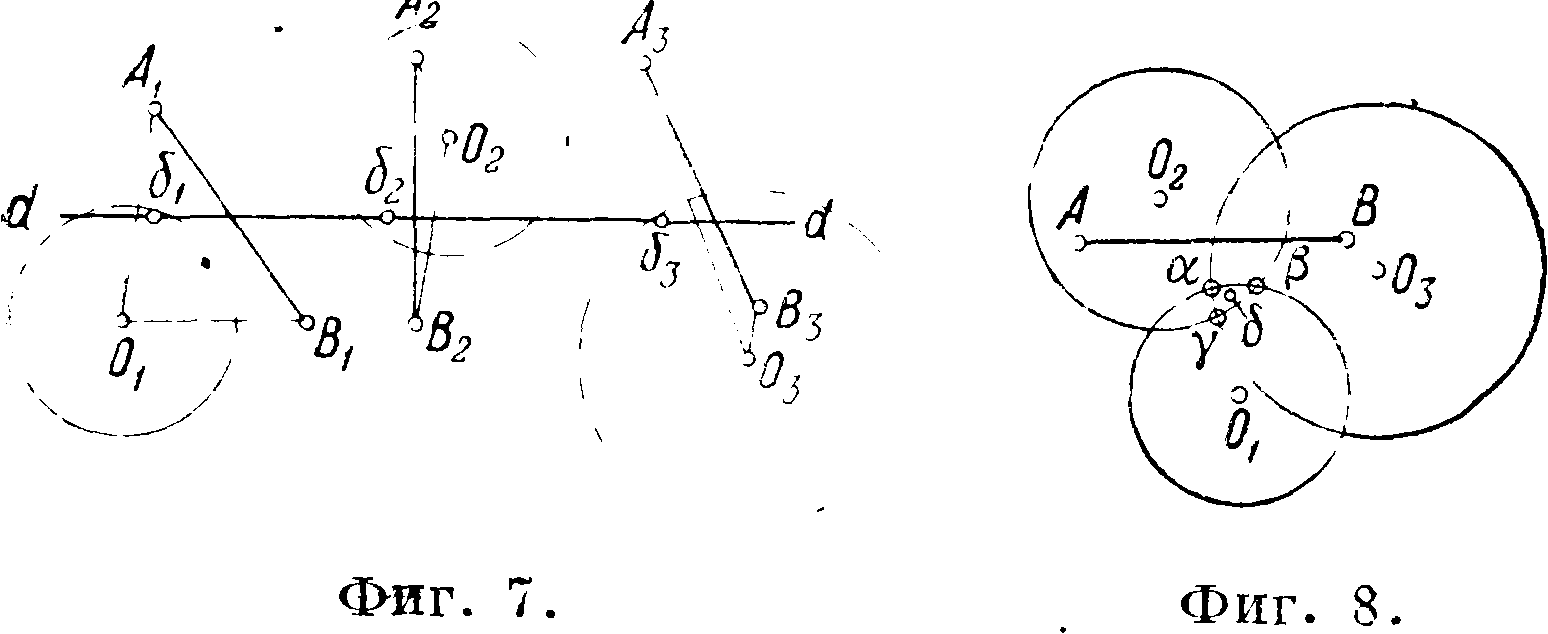
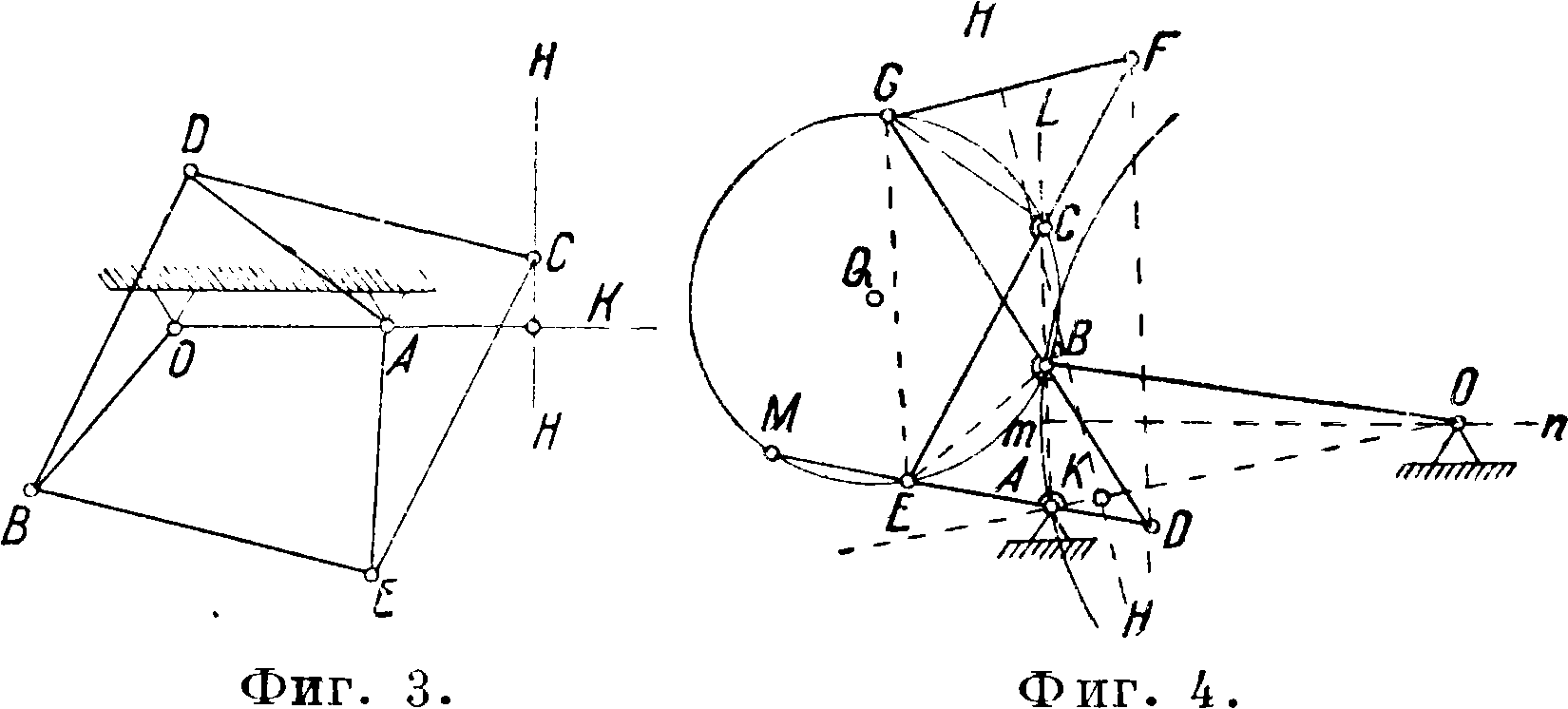
прямой НИ, перпендикулярной к АО. Подобное же движение м. б. выполнено механизмом отрицательного инверсора Поселье (фигура 3).

Аналитич. решение задачи об использовании инверсии в механизмах приводит к использованию метода комплексной переменной, дающему исчерпывающее решение этой задачи в общем виде (работы Лурье, Лойцянского и др.).

Точный Ш. н. м. сист. Гарта (фигура 4) должен удовлетворять условию DE=FG, DG=EF и О А=ОВ. В этом механизме точка С движется по прямой НИ, перпендикулярной к АО. Для воспроизведения этого движения точки С

I Решение задачи о приближенных III. н. метров. сводится к решению задачи о нахождении в I звене механизма точек, траектории которых j были бы близки к прямой линии. Т. к. точки

звена, лежащие в данный момент на окружности поворотного круга или близ него, имеют для этого момента радиусы кривизны своих траекторий равными бесконечности или близкими к ней, то нахождение точек, движущихся по приближенно прямолинейным траекториям, м. б. выполнено следующим графич. приемом. Пусть требуется найти подобную точку на зве-i не АВ, движущемся концами по своим траекто-! риям. Берем крайние положения А₁В₁к А₃В₃; (фигура 7) и какое-либо промежуточное A ₂В₂ зве-1 на АВ и строим для всех этих положений пово-! ротные круги с центрами О_х, 0₂ и 0₃. Точки j звена, которые за все эти положения двигаются приближенно прямолинейно, должны лежать

строим фигуру EFGD, удовлетворяющую вышеуказанным равенствам. На звене ED закрепляем произвольную точкуА,проводим AL DF, отмечаем точки В и С пересечения этой параллели со звеньями DG и EF и соединяем точку В с точкой О, лежащей на перпендикуляре тп. восстановленном из середины АВ. На фигуре 5 дано преобразование механизма Гарта для точки А, выбранной вне звена DE.

Точный Ш. н. м. сист. Эванса (фигура 6) должен удовлетворять условию:

ОС=АС=ВС=

В этом механизме точка В движется по прямой НИ. Данный механизм является направляющим, но не шарнирным, т. к. в нем имеется в точке А. поступательная пара, и указывается как имеющий практич. применение. или на построенных окружностях или вблизи них. Для определения этих точек совмещаем положения А₁В₁, А₂В₂ и А₃В₃ вместе с поворотными кругами так, чтобы совпали крайние точки звена (фигура 8). При этом выделится участок αβγ, одновременно принадлежащий трем поворотным кругам. Выбрав в этом тр-ке точку δ, равно отстоящую от всех поворотных кругов, и вычертив ее траекторию, получим, что эта траектория будет почти прямой, т. к. точка δ за все три положения весьма близко находится от окружностей поворотных кругов. Если тр-к αβγ оказался бы чрезмерно большим или если бы круги не пересеклись между собой,

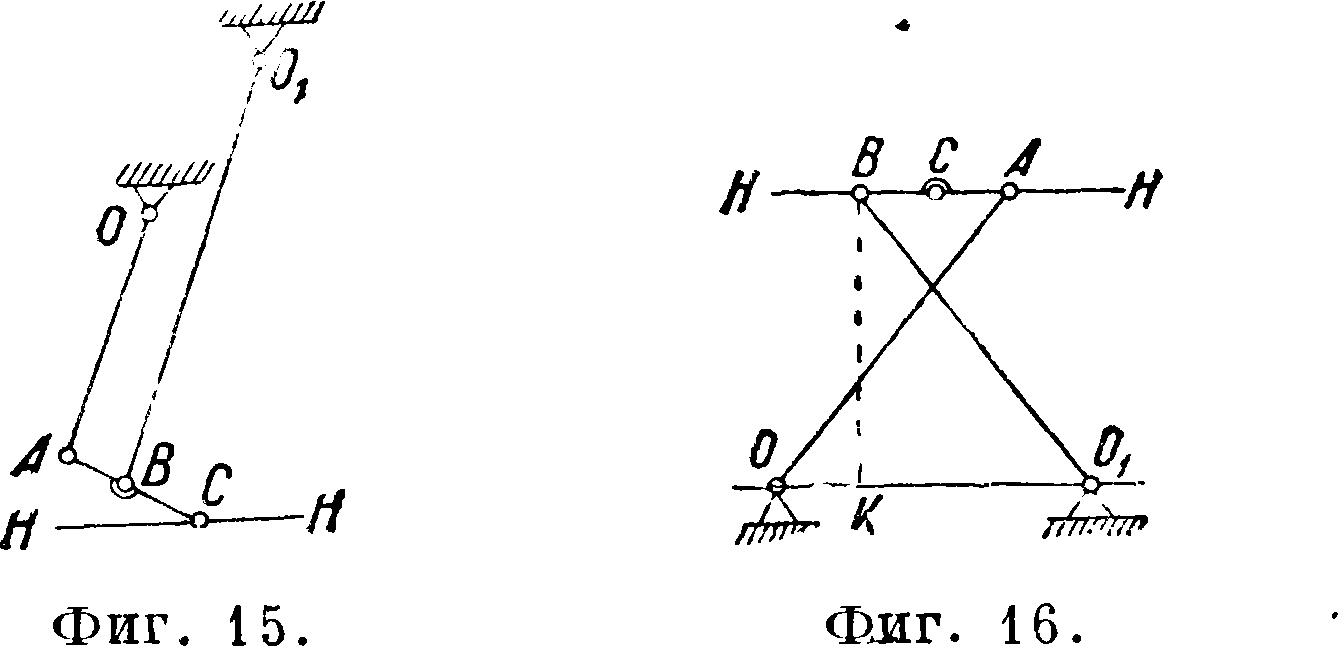
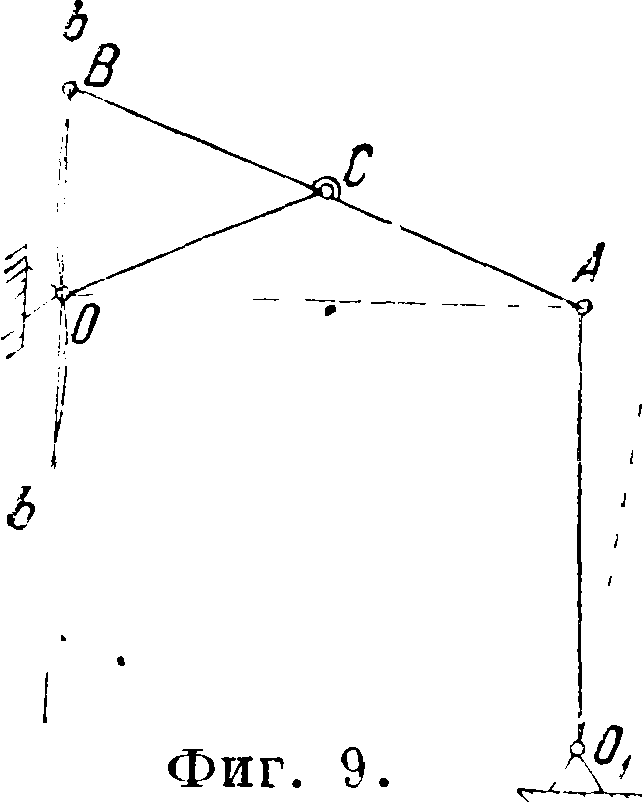
то необходимо было бы исследовать другие положения отрезка АВ. При выборе точки δ в точках а, β или γ получаем прямолинейное движение за два соответствующих момента. На фигуре 9 показан приближенный Ш. н. м. системы Эванса, полученный из точного (фигура 6)

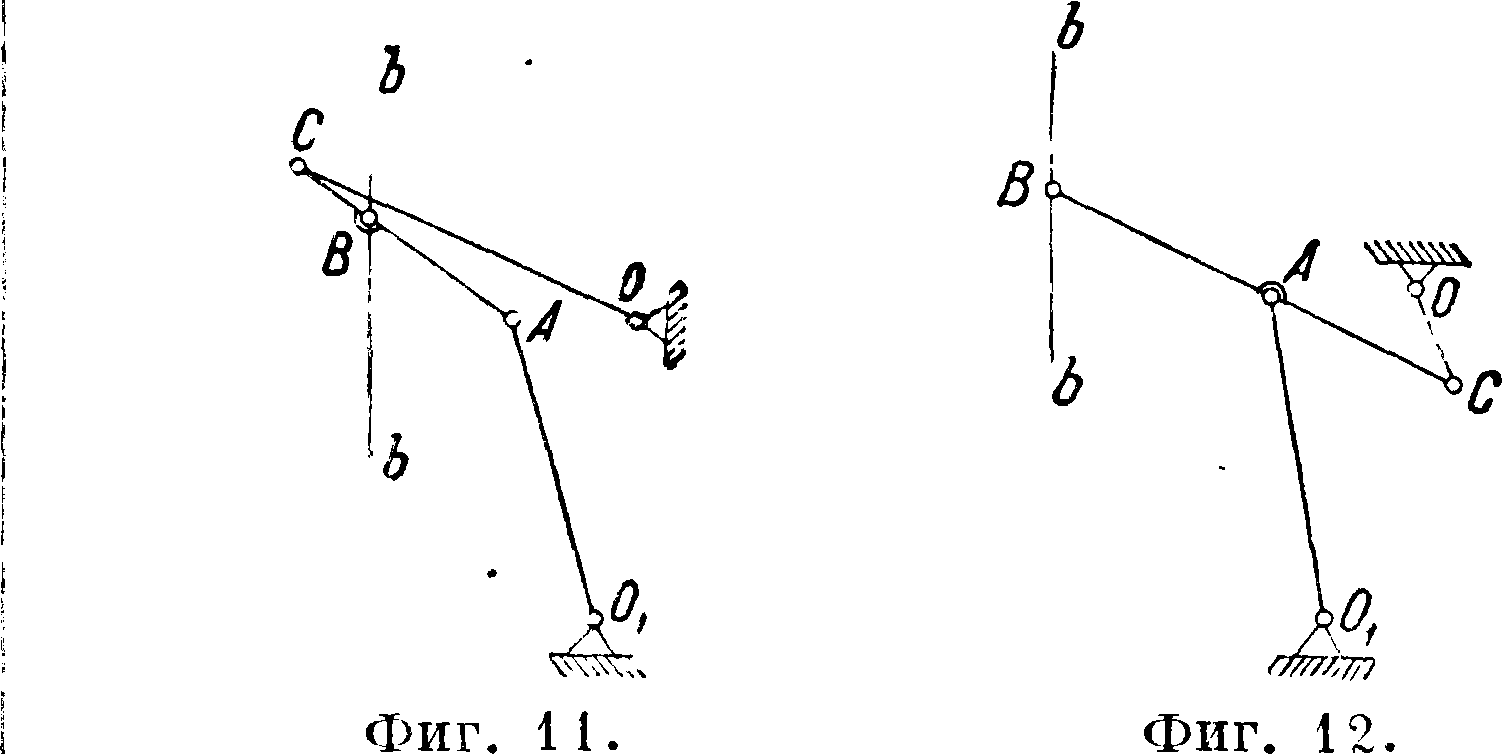
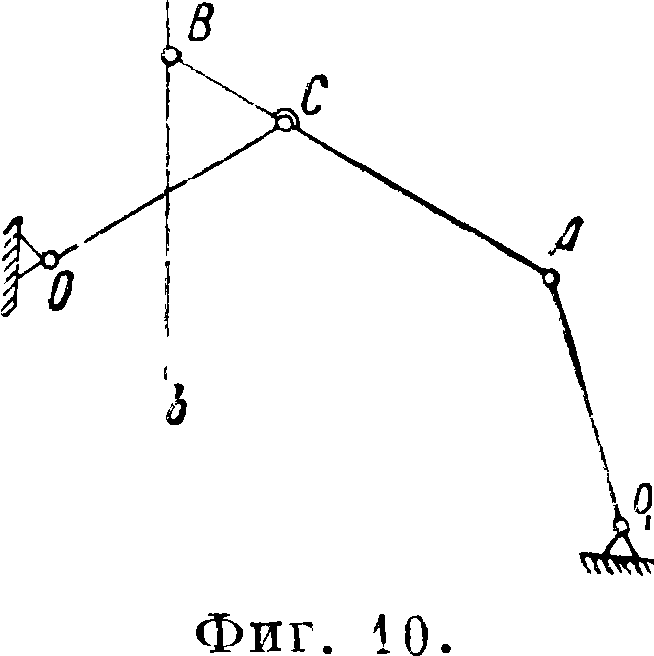
путем замены поступательн. пары парой вращательной в точке О_х и звеном О_гА, имеющим значительную длину. В этом механизме незначительные перемещения точки i от влево дают значительные перемещения точки В по траекториям, весьма близким к прямой. Этот механизм находит себе применение в различных самопишущих приборах. Ведущая точка С звена АВ Ш. н. м. сист. Эванса м. б. выбрана и не по середине звена АВ, а ближе к точке В (фигура 10), или же, как это показано на фигуре 11 и фигура 12, за точками А и В.

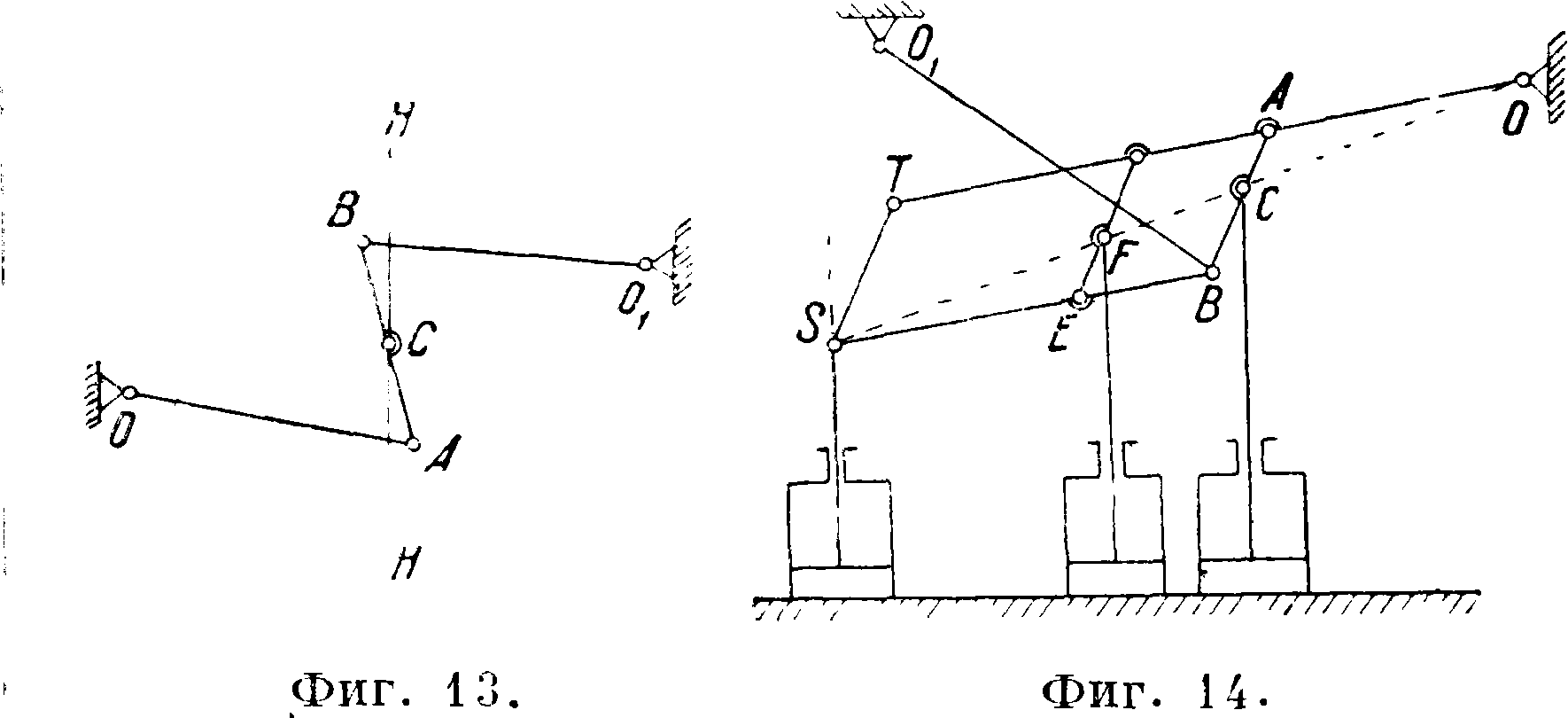
К приближенным Ш. н. м. принадлежат механизмы Уатта (фигура 13 и 14); см. Параллелограмм Уатта. Здесь по приближенным прямым двигаются точки C,F я S. На фигуре 15 дан ТТТ- н. м. сист. Уатта с центрами О и 0₁₉ лежащими по одну сторону от прямой НИ. В этом

Фигура 17.

механизме все соотношения остаются теми же, но точка С делит внешним образом отрезок АВ на части, обратно пропорциональные длинам рычагов. Механизмы Уатта часто носят название лемнискатных Ш. н. м., так как точки звена АВ имеют своими траекториями лемнискаты.

Акад. Чебышевым был предложен целый ряд механизмов, из которых нек-рые необходимо отметить. Перекрестный шарнирный направляющий механизм дан на фигуре 1G с наиболее удобными соотношениями звеньев:

ООг: ОА : О_гВ : АВ=4:5:5 : 2.

При движении механизма середина звена АВ точка С—описывает траекторию на большом протяжении, мало отличающуюся от прямой. Опустив из точки В на 001 перпендикуляр ВК, нетрудно убедиться, что стороны тр-ка ВКО_г. относятся между собой, как

КОг.ВК.ВОг^ 3:4:5.

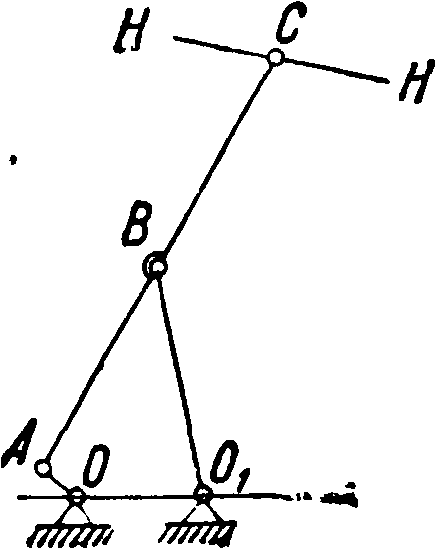
На фигуре 17 изображено т. н. прямило Чебышева. Точка С механизма движется по приближенной прямой ЯН при перемещении точки А по некоторой дуге. Наиболее удобным соотношением является следующее:

АВ=ВС=ВО г — 64; О А=11 и ОО_л=25.

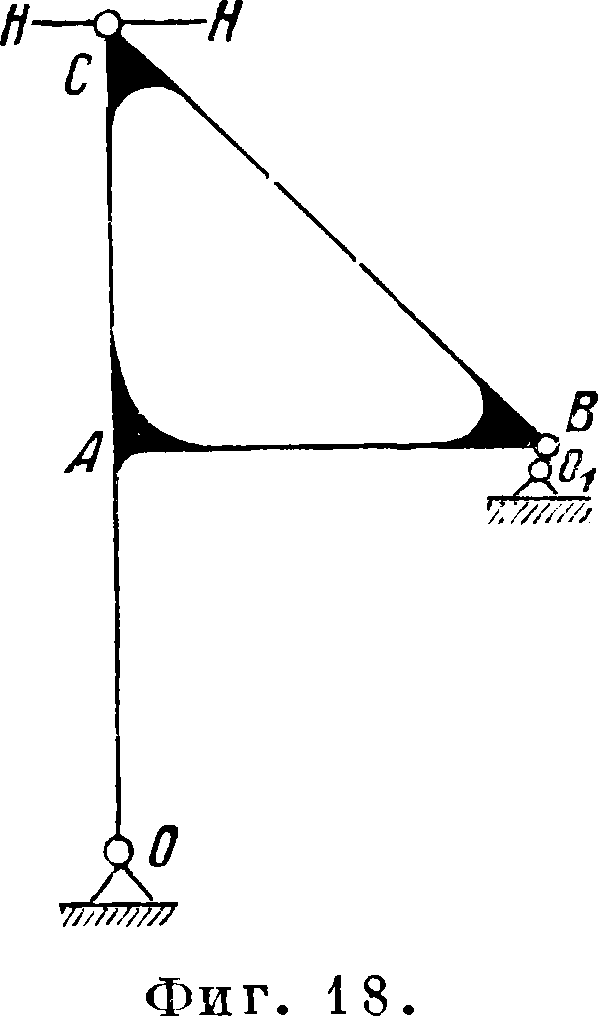
На фигуре 18 изображен непрерывный трансформатор Чебышева. Точка С механизма движется по прямой НН при перемещении точки В по целой окружности около точки О_г. Наиболее удобным соотношением является следующее:

ОА=АВ=АС=100; 00^141 и О_хВ^b.

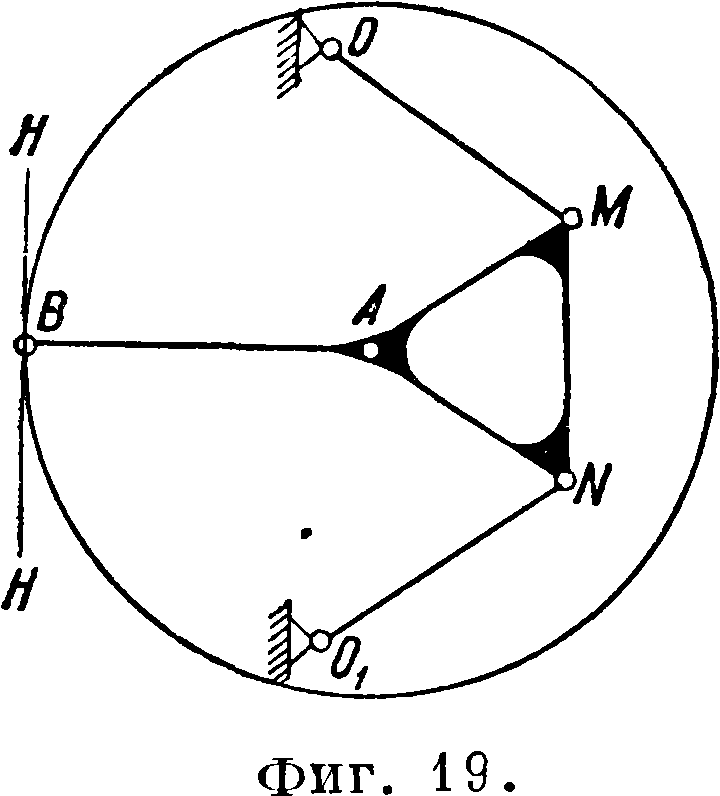
Тр-к АВС жесткий с прямым углом при точке А. На фигуре 19 показан механизм тр-ка

Робертса. Прямолинейную траекторию описывает точка В. Ведущими точками являются точки М и N, расположенные внутри малой окружности Кардана, симметрично относительно диам. ВА.

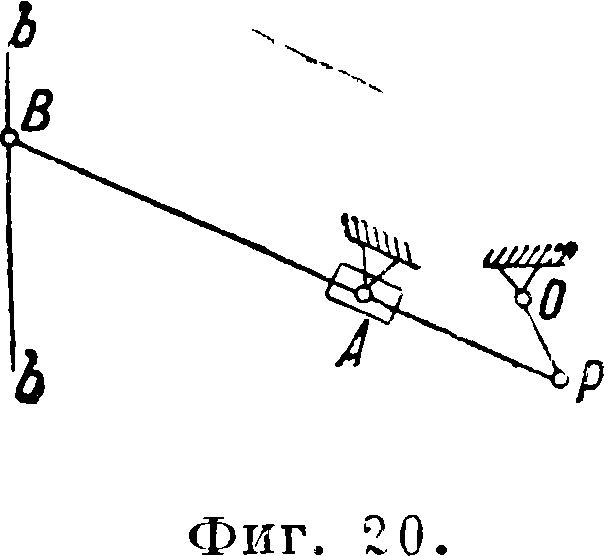
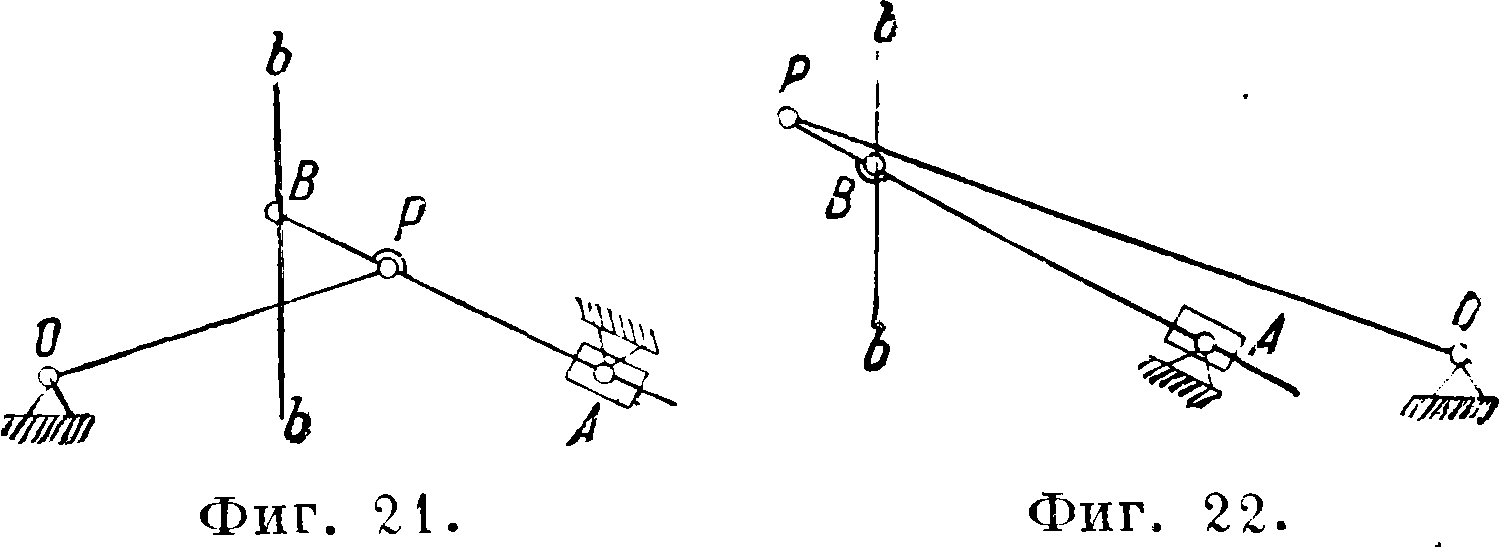
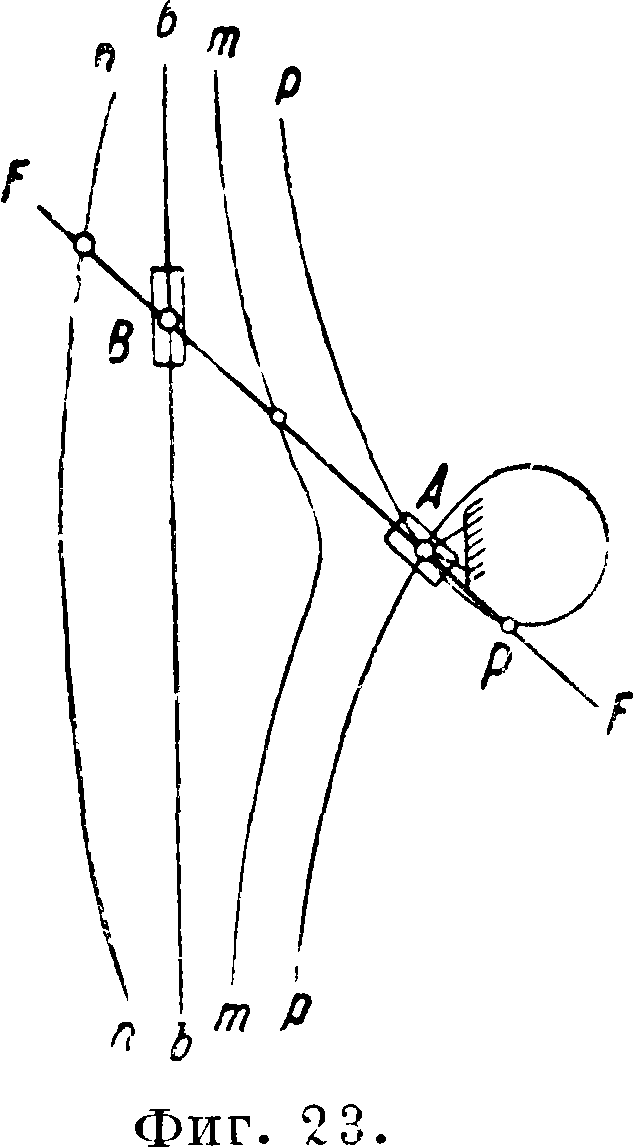
Необходимо отметить нек-рые направляющие механизмы, в которые кроме шарниров входят и пары поступательные. К числу этих механизмов относится группа конхоидальных направляющих механизмов (фигура 20, 21 и 22). Эти механизмы имеют прямолинейно движущимися точки В и основаны на том, что если звено FF (фигура 23) движется так, что проходит через неизменный центр A, a его точка В движется по некоторой прямой bb, то отдельные точки прямой FF описывают кривые тт, пп., рр, называемые конхоидами, имеющие различные очертания в зависимости от выбора точки на звене АВ. Если, обратно, заставить прямую FF проходить через точку А, а какую-либо точку, например Р, двигать по конхоиде рр, то точка В будет двигаться по прямой. Участки конхоид м". б. без больших погрешностей заменены дугами окружностей, тогда получаем ряд различных схем механизмов (фигура 20, 21, 22). Впервые эти механизмы были построены Рей-хенбахом. К числу направляющих механизмов, с введением одной высшей пары, относится механизм Картрайта (фигура 24). Здесь прямолинейное движение точки С осуществляется введением двух зубчатых секторов. В этом механизме 01/1=0₂В, АС=ВС и оба сектора равны между собой.

Обратными Ш.н.м. называются механизмы, полученные из Ш. н. м. путем обращения движения. Если в каком-либо механизме

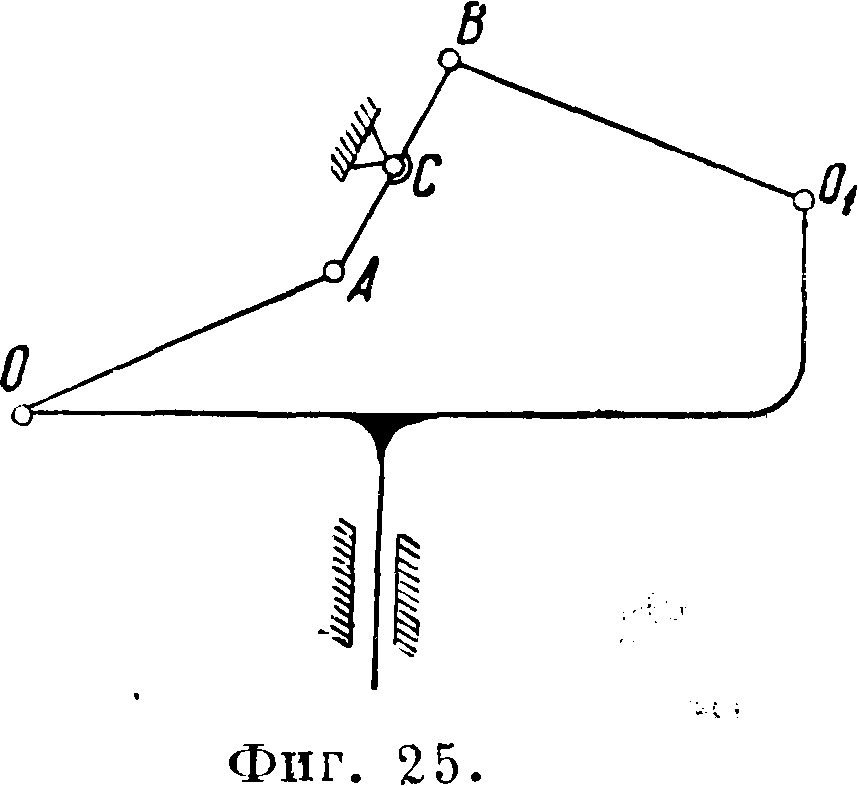
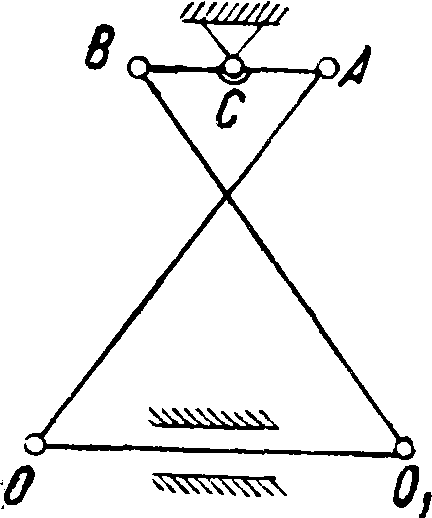
какая-либо точка движется прямолинейно-поступательно относительно неподвижного звена, то "можно, закрепив эту точку, получить прямолинейно-поступательное движение звена, ранее бывшего неподвижным. Таким образом были получены обратные Ш. н. м. систем Эванса, Картрайта, Чебышева и др. На фигуре 25 дан обратный механизм Уатта, а на фигуре 26 обратный механизм Чебышева.

Среди пространственных III. н. м, необходимо отметить сферические Ш. н. м. В этих механизмах отдельные точки двигаются не по прямым, а по дугам, лежащим в различных плоскостях, секущих сферич. поверхность. Теория их построения сводится к отысканию вышеуказанных ранее приемов точек плоского механизма, имеющих своими траекториями

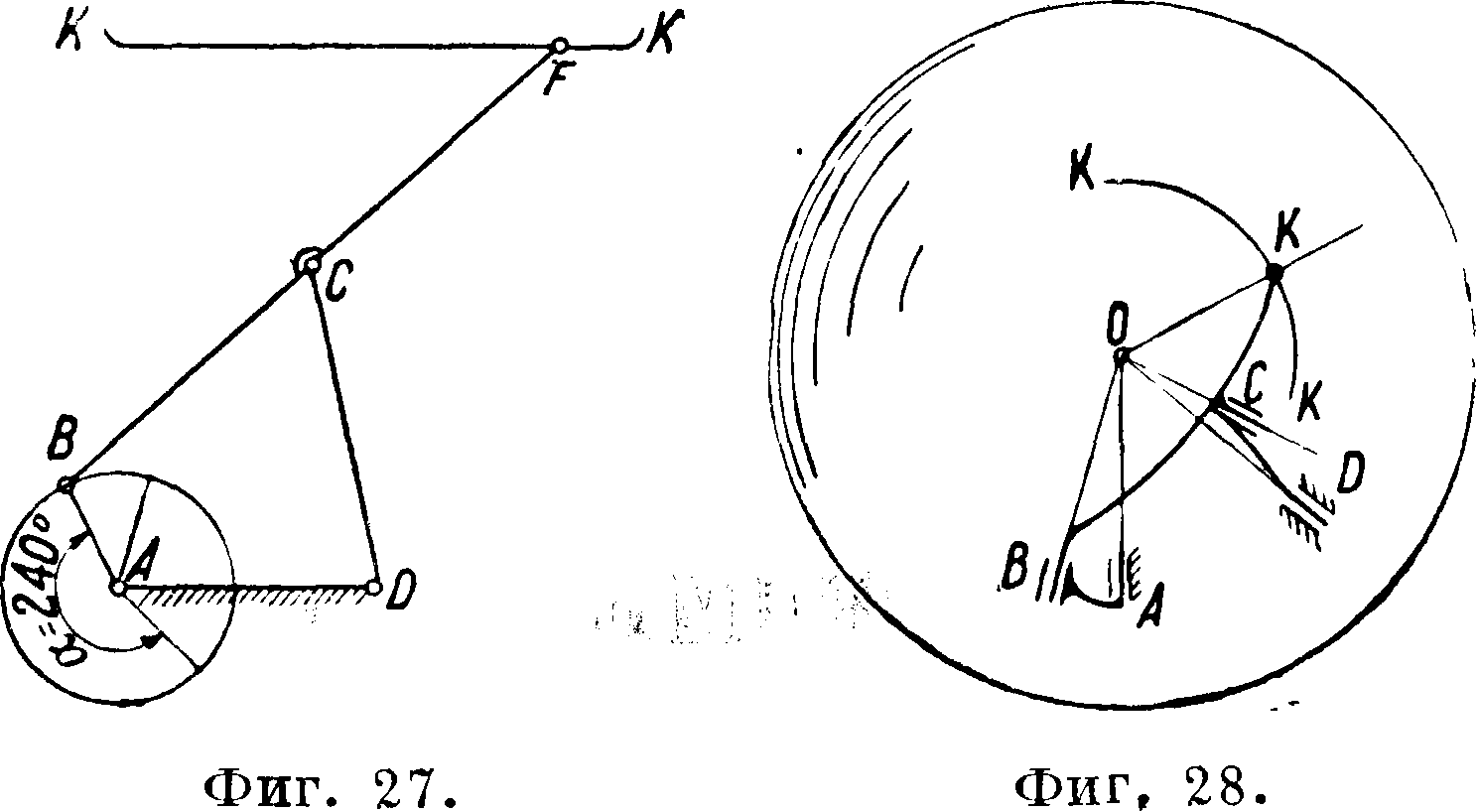
приближенные прямые, и к переносу полученных механизмов с сохранением выбранных соотношений на сферу. Все точки, которые в плоскости механизма двигались по прямой, в перенесенном на сферу механизме будут перемещаться по дугам окружностей сферы. Подобным образом м. б. построены сферические механизмы, аналогичные вышеуказанным плоским. Из числа сферич. Ш. н. м. можно указать механизм, предложенный И. Артоболевским. Этот механизм на плоскости (фигура 27) аналогичен прямилу Чебышева (фигура 17) и отличается от него соотношением звеньев AB : AD : ВС : : CD :=11 : 25 : 32 : 32 : 32, а также тем,

I что прямолинейная часть траектории точки F I параллельна неподвижному звену AD и соот-I ветствует повороту кривошипа АВ на 240°. На сфере этот механизм описывает дугу КК (фигура 28), имеющую различную величину в за-, висимости от выбранного радиуса сферы.

Из указанных Ш. н. м. практическую важность представляют только немногие, так как обилие шарниров делает эти механизмы легко расшатываемыми, что отзывается на точности их движения. Их применение ограничивается главным образом областью приборостроения и теми случаями, когда необходимо преобразовать вращательное движение в поступательное без применения поступательных кинематических пар.

Лит.: Мерцалов Н., Кинематика механизмов, М., 1916; Зернов Д., Прикладная механика, Л., 1925; Рузский Д., Кинематика машин, Киев, 1908; Чебышев П., «Изв. Петербургской академии наук», СПБ, 1881; Лурье А., К теории приближенных шарнирных направляющих механизмов, «Журн. прикладной физики», М.—Л., т. 2, вып. 3—4; Лойц янский Л., О нек-рых свойствах движения Watt’а, «Изв. Ленинградского поли-технич. ин-та», Л., 1927, т. 30; Артоболевский И., Синтез и кинематич. анализ сферич. механизмов, «Труды ин-та с.-х. машиностроения»,‘1933, вып. 1; D а г-Ь о и х G-., «Bull, des sciences matMmatiques», P., 1879, t. 3, p. 151. И. Артоболевский.