> Техника, страница 93 > Эйлера уравнения

Эйлера уравнения

Эйлера уравнения, ур-ия, встречающиеся в различных отделах математич. анализа, теоретической и прикладной механики, гидродинамики ит. п. и установленные впервые великим математиком Эйлером. Важнейшими из них являются нижеследующие ур-ия. В мате-

м а т и к e. 1) Диференциальное ур-ие следующего вида:

α_όχ

dⁿy

dxⁿ

-f- (ΧχΧ^η

dⁿ~)y dxⁿ~ i

+ a₂x^{n 2}

dⁿ~*y dxn~ 2

+

+. + a_n-i^x ^ + и_пУ — (1)

где α₀, α_χ, α₂, ., —нек-рые постоянные. Пусть имеется, с другой стороны, алгебраич. ур-ие: а_п + + «я-2^ (* - 1) +

+. + α₀ζ (ζ — 1) (ζ — 2). (ζ — η + 1)=0. (2) Если ζ_μ— какой-либо корень ур-ия (2), то частным интегралом ур-ия (1) будет

У μ=ΟμΧ~^ΖΡ (μ=1, 2,., η), где Сμ—произвольные постоянные. Если все корни ур-ия (2) различны, то общий интеграл ур-ия (1) будет _п

у=Ci®*¹ + C_ZX^Z* +. + C_nX^Zn=2 ΟμΧ^ΖΡ.

μ=1

Если из числа п корней ур-ия (2) ν корней равны между собой, т. ч.

ζ₁=ζ₂=.=ζ_ν=ζ,

а остальные корни различны, то общий интеграл ур-ия (1) будет равен у=[С₀ + С₁]пх-{-С₂(1пх)² +. + C_v(lnx)^v] x^z -f + C_v+l x^zv+1 +. + C_nx^Zn.

2) Равенства, или ф-лы, Эйлера соз х -f г sin х=е^гх ( cos х — г sin х=е~^2Х f

получаемые разложением

ный момент), то ω =

в ряды тригонометрии. и показательных ф-ий (смотрите Дифференциальное исчисление).

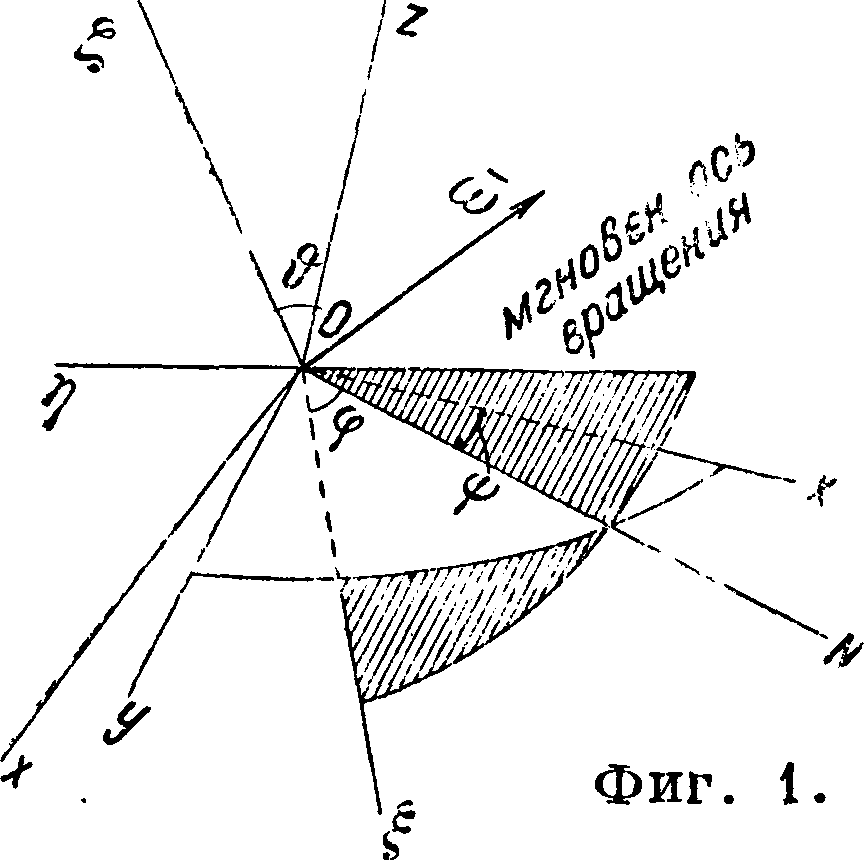
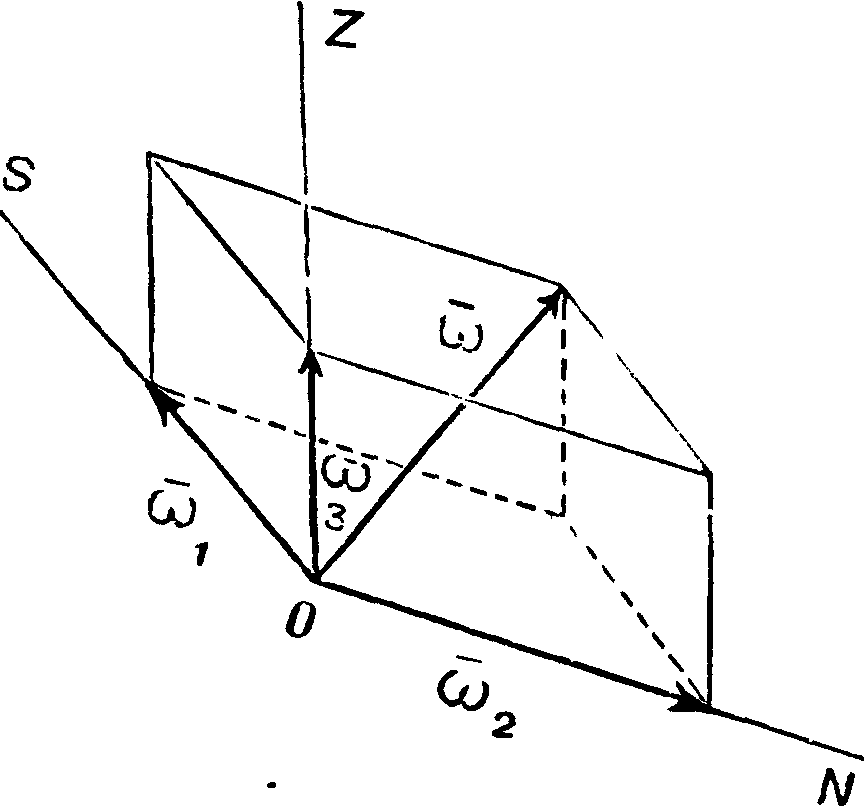
В теоретической механике. Если тело вращается вокруг неподвижной точки О с угловой скоростью, вектор которой равен со (линия действия вектора совпадает с мгновенной осью вращения вдан-*i + со₂ + (о₃, причем #. dy>

7’ ^ω·³ “ dt ’

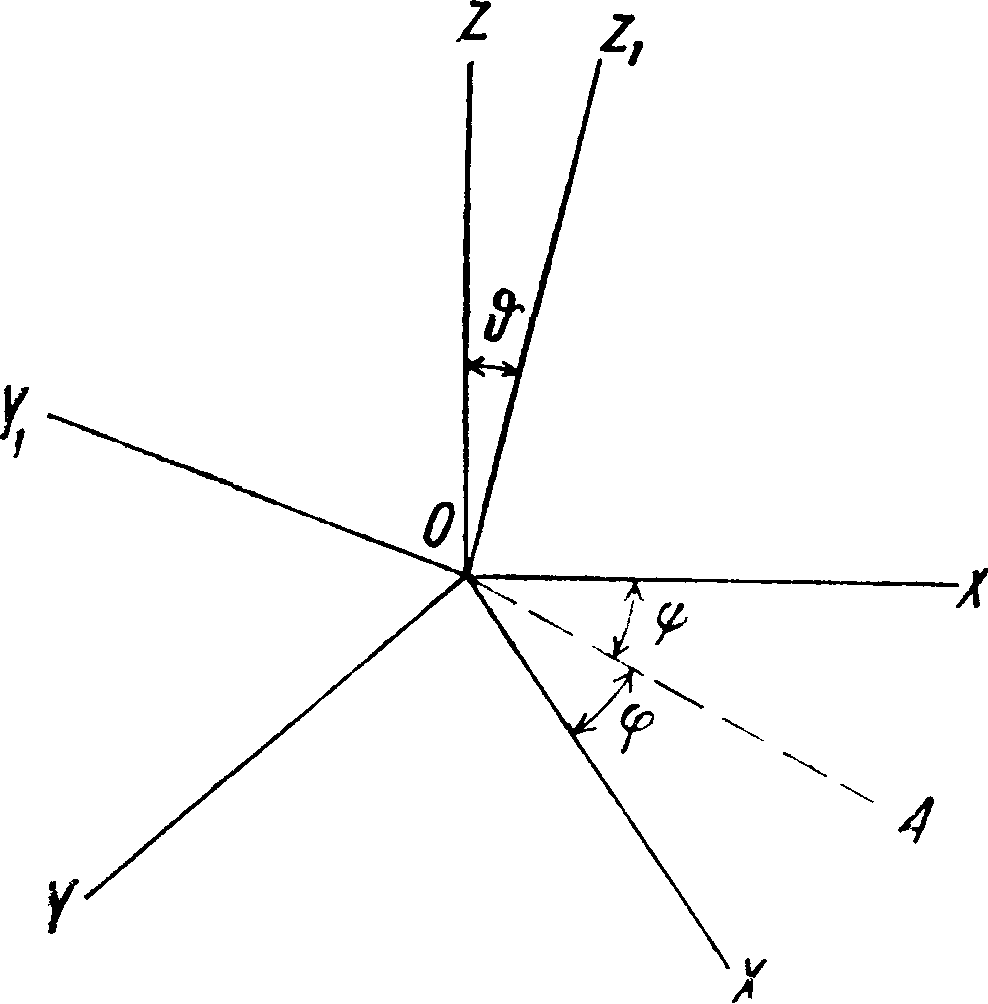
где ω_ΐ9 со₂, cog — компоненты по направлениям С, ΟΝ. z (фигура 1 и 2), а φ, гр и #—эйлеровы углы (смотрите). В свою очередь спроектируем векторы оо_ь со₂, со₃ на оси ξ, η, £, обозначив компоненты векторов по этим осям соответственно через р_и q_if r_x р₂, q₂, r₂ p_z, q₉, г₃; при Этом получаем непосредственно:

Ρι=0; 2ι= 0; 4 =

d9 d».. _n

p₂=^co$φ; g₃=-_ssmf, r₂=0.

Вектор же ω₃ разлагаем в свою очередь предварительно по направлению оси С и по перпендикулярному к этой оси направлению, то есть по направлению, перпендикулярному к прямой ON, после чего получаем:

P3=-^sin#sm9>; q₃=^ sin ϋ соз ψ. r₃=^cos&.

T. к. проекция равнодействующего вектора на какую-либо ось равняется сумме проекций со ставляющих вектора на ту же ось, то имеем, обозначая проекции ω на оси £, η, ζ через V, i, г:

P=Pi + Pi + Pi=™^C0S<P + ^ySin 0 sin φ,

2=2i + 2a + 2з=~^ sin Ψ + 37 sin ^{& cos} Ψ r=ri + r₃ + r₃=cos 0.

Это—кинематич. ур-ия вии с этим имеются еще ющие динамич. закон движения твердого тела около своей неподвижной точки. Допустим, что такое тело находится под воздействием внешних сил JFV F₂,F_i4., точки приложения которых определяются относительно точки О радиусами - векторами г_г, г,. Возьмем,

Эйлера. 3 ур-ия,

В соответст-устанавлива-

Фигура 2

какой-либо элемент тела, массак-рого равна dm_itк которому приложена внешняя сила и равнодействующая всех внутренних сил ^-.Применяя к этому элементу теорему моментов (смотрите Механика теоретическая), имеем, обозначая моменты сил Fj и Fi относительно О через Mi и Ж ·:

d · г

Mi + JM _t=[Fi · η·] + [Fi · г _{= _ж [dm/vpi]

где Vi—векторная скорость элемента. Т. к. сумма моментов всех внутренних сил относительно какой-либо точки равна нулю, то

М — 2 -М"е=f Jt l^dmi ^vi^rA - J где M—главный моментный вектор системы внешних сил относительно О; интеграл в правой части взят по всему объёму тела. Проектируя обе части последнего равенства на ось х и опуская индексы, имеем

M.-S Л™ уШ~^гжф

С другой стороны, имеем г? — [cor]

и следовательно:

ν_χ=-_άΤ=^ω2Ζ-ω*ν,

dv

ν_ν=_1ϊ=^ω3^χ-ω₁ζ,

dz

dt

-=co_xy — ω₂Χ.

Взяв вторые производные, получаем

М_х=J dm (у² -f z²) + ω₂ω₃ {у² — z²) 4-

+ 2^’ У^е> ^Ζχ^=ΊΓι J ^dm № ^{+ +}

+ ω₂ ω₃ J dm (У^г - z°-) + J dm У^{2 ΖΧ)}·

Так как

J dm (у² + .г²)=Ι_χ; J (?/² - ^·²)=~ ly*

где I_x, Iу и I_z—моменты инерции тела относительно осей х_у у, ζ, то м,=14?+ е.

+ J* dm 2 _г (^ХУ> У⁰9

Если за неподвижрше оси взять мгновенное положение главных осей инерции тела относите ль-

но точки О, то последний член равенства, как представляющий сумму центробежных моментов инерции тела относительно главных осей, будет равен 0 (смотрите Моменты инерции). Применяя при этом прежние обозначения для про-екций угловой скорости, имеем:

I_x^ + (I_e-I_y)qr=M_X!

I_tJ^ + (I_x-L·) rp=M_y,

^% + {ΐ_υ~^Ι,)να=Μ_ι.

Это—динамич. ур-ия Эйлера (смотрите Прецессия).

В гидродинамике ур-ия Эйлера определяют аналитич. условия движения жидкости и в частности условия ее равновесия.

Помимо вышеприведенных Э. у. имеется еще целый ряд ур-ий, которые были впервые выведены другими лицами, исходившими из тех или иных положений, установленных Эйлером, например уравнение Эйлера-Пуассона, Эйлера-Са-

Вари И Т. Д. М. Серебренников.

Лит.: см. Механика теоретическая и Гидродинамика.