Эксцесс

Эксцесс, сферический избыток, ε, превышение суммы углов сферического тр-ка над 180°:

_е=А + Б + 180°,

где А, В, С—углы сферич. тр-ка (смотрите Тригонометрия). Если известна площадь Р сферич. тр-ка, то Э., выраженный в ск. дуги, найдется по ф-ле р"=^Р

ti*smi" ’

где R—радиус сферы.

Э. находит себе большое практич. применение в геодезии при решении тр-ков триангуляционной сети высших классов. Если длины сторон тр-ков меньше 10 км (триангуляция 3, 4 и 5 классов), то тр-ки могут считаться плоскими и Э. их не вычисляется. При длинах сторон, бблыних 10 км, уже приходится иметь дело со сферич. тр-ками. Решение сферич. тр-ков в практике СССР производится обычно по теореме Лежандра, устанавливающей, что сферич. тр-ки с малыми относительно радиуса шара сторонами можно с совершенно достаточной точностью вычислять как плоские; необходимо лишь все углы А, В, С данного сферич. тр-ка заменить приведенными плоскими углами А_х, В_1} С_г по ф-ле:

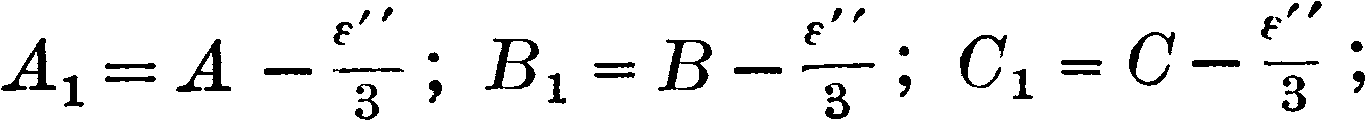
причем при обычных размерах сторон 12—60км (триангуляции 1 и 2 классов) величина Э. вычисляется по ф-ле

_ b · с · sin А ⁸ ~~~ 2R²sin 1" ’

где b и с—длины сторон измеренного сферич. угла А. При длинах сторон 60—250 км величина Э. вычисляется по ф-ле

b· с· sin Αχ /X т² ~2К² sin 1" * ^{l +} 8R² j ’

где

α² + b² + с²

m²=—^{τ τ} ·

При длинах сторон, бблыних 250 км, приходится иметь дело уже со сфероидич. тр-ками, и перевод углов и вычисление Э. производятся по другим усложненным ф-лам. В триангуляции 1 и 2 классов Э. вычисляется по четырехзначным логарифмам, и величина _г, бе рется по аргументу широты места из специальных геодезич. таблиц (Шарнгорста или Ур-маева). Для равностороннего тр-ка Э. имеет следующие примерно величины (в ск. дуги): при длине стороны Ь=30 км ε"^2", при b== 60 км e"s=8", при δ =111 км ε"^24".

Лит.: Красовский Ф., Высшая геодезия,

ч. 2, Л., 1932; У р м а е в Н., Руководство по обработке триангуляций, М., 1932; Филоненко А., Практическое руководство для производства триангуляции 3, 4 и 5 классов, вып. 1, М., 1927; Витковский В., Практическая геодезия, 2 изд., СПБ, 1911; Цингер Н., Курс высшей геодезии, СПБ, 1898; Лавров В., Сферическая тригонометрия, М., 1915; Дитц О., Сферическая тригонометрия, М., 1925. Н. Веселовский.