> Техника, страница 97 > Электрические фильтры

Электрические фильтры

Электрические фильтры, устройства, состоящие из ряда электрических цепей, включенных в определенном порядке и позволяющие разделять, выделять или удалять по определенным законам токи различных частот. Действие Э. ф. основано на изменении свойств электрических цепей, из которых они состоят, в смысле пропуска ими токов различных частот или частотных полос, лежащих в различных участках частотного спектра. Э. -ф. пропускают токи определенных частот с малым затуханием или даже без изменения их первоначальной силы и практически не пропускают, поглощая совершенно токи других частот. Схематически Э. ф. состоят из ряда емкостный или индуктивных сопротивлений, включенных частью параллельно, частью же последовательно. Свойства Э. ф. и определяются поведением этих сопротивлений при различных частотах. Самый простейший Э. ф. состоит обязательно хотя бы из одного последовательного и одного параллельного сопротивления. Такой простейший Э. ф. называется ячейкой, звеном или секцией. Обычно Э. ф., применяемые на практике, имеют ряд этих ячеек и называются ячеечными (или многоячеечными). Э. ф. обыкновенно включаются между ка-ким-йибо источником тока и приемником этих токов; т. о. в этом отношении они представляют собой обычный четырехполюсник (смотрите Телефонная передача) (фигура 1). Действие Э. ф, во многих отношениях аналогично действию избирательных резонансных контуров, которые состоят из индуктивности и емкости. Мало того, действие многих Э. ф. базируется на свойствах резонансных контуров. Однако между одиночными резонансными контурами и Э. ф. имеются и существенные различия, выявляющие особенности Э. ф. Кривая потерь в зависимости от частоты для резонансного контура (или ряда слабо связанных контуров) имеет V-образный характер. Минимальные потери контур дает при резонансной частоте для последовательного включения в линию передачи при последовательном соединении емкости и индуктивности и для параллельного включения относительно линий при параллельном соединении емкости и индуктивности. Характер

V-образности кривой контура выявлен тем резче, чем ниже частота. Наклон боковых сторон кривой зависит исключительно от так называемым «множителя напряжения» катушек, примененных в контуре, определяемого отношением coL/R.

В Э. ф. зависимость потерь от частоты выражается обычно U-кри-вой (фигура 2), при этом Нс&ЛОН боковых сторон зависит от вида Э. ф. (его схемы) и источит Фильтр го—_

Фигура 1.

приемник

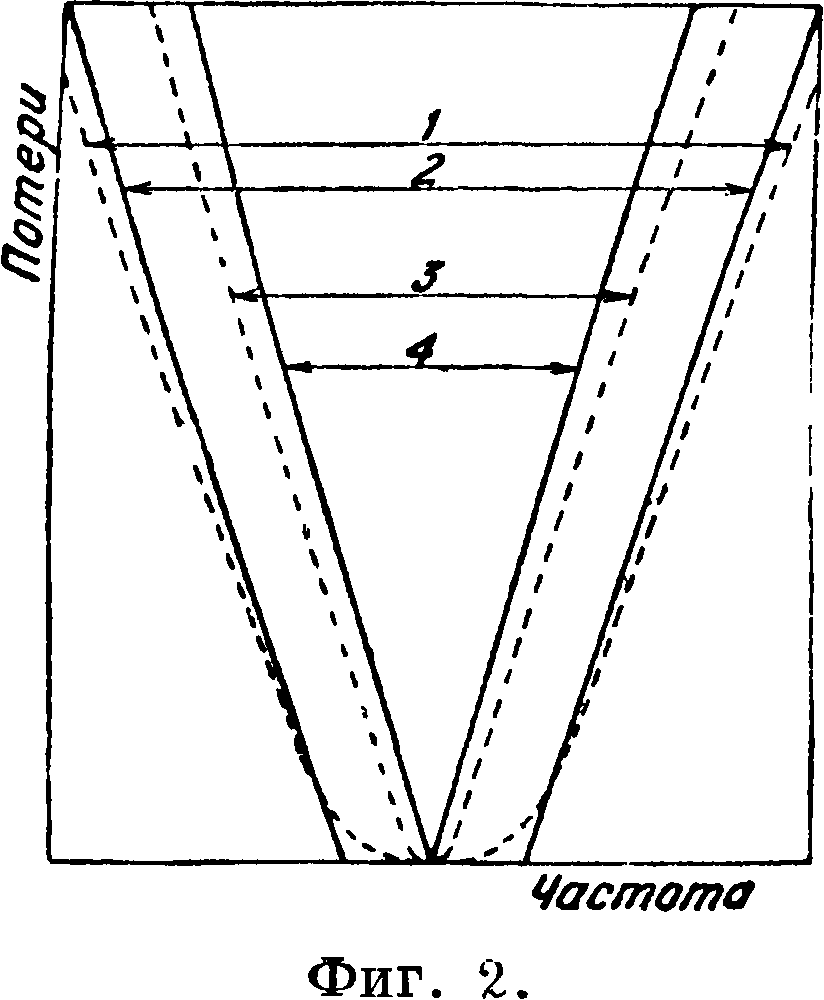
числд ячеек в нем. Характер нижнего участка U-кривой (его ширина и прямолинейность) зависит от «множителей напряжения» катушек и конденсаторов, примененных в Э. ф., то есть от отношений coL/R для катушек и ^ для конденсаторов. Эти типичные различия контуров и Э. ф. в наглядной форме показаны на фигуре 2, где 1 — Э. ф. с омич, сопротивлением, 2 — Э. ф. без омич, сопротивления, 3 — контур с омич, сопротивлением, 4 — контур без омич, сопротивления. В соответствии с этими основными свойствами резонансных контуров и Э. ф. области их возможного применения разграничиваются следующим образом. Э. ф. применяются обычно до частот порядка 500 000 Hz, при частотах более высоких их конструирование наталкивается на очень большие практические трудности. Поэтому на высоких частотах для избирательных целей применяются гл. обр. самостоятельные резонансные контуры или ряд контуров, включенных каскадом и связанных соответствующим образом друг с другом. Однако делаются попытки, с одной стороны, распространить применение Э. ф. в их настоящем виде в область самых высоких частот, а с другой,—применить контуры на низких частотах, в особенности для получения узких частотных полос пропускаемое™. В настоящее время удается уже путем нек-рого видоизменения обычных форм Э. ф. конструировать ячеечные Э. ф. для очень высоких частот порядка нескольких 10⁶ Hz (смотрите ниже). Теоретически во многих случаях практического применения резонансные контуры очень удобно могут рассматриваться как частный случай Э. ф.

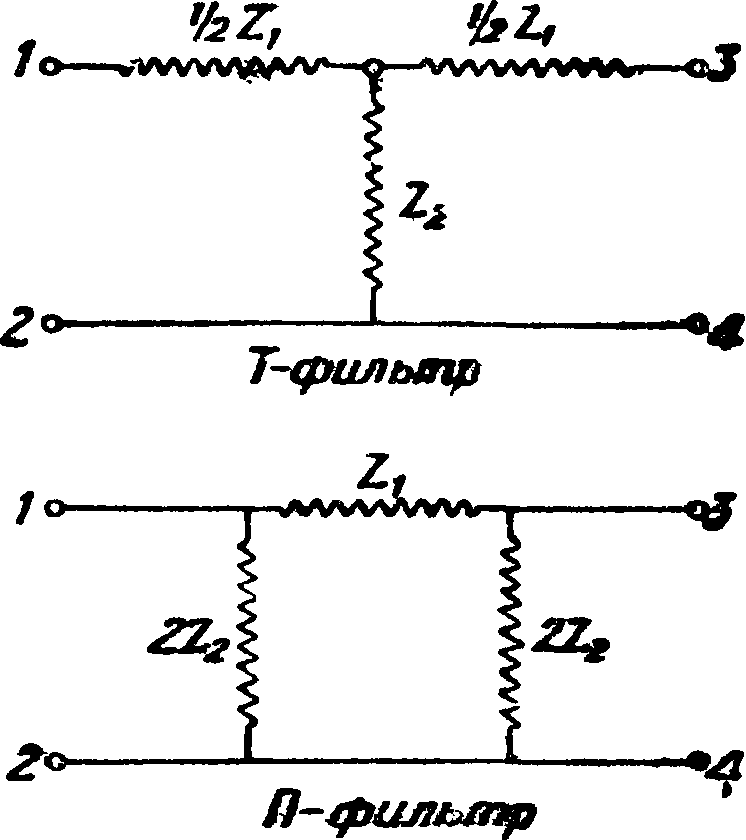
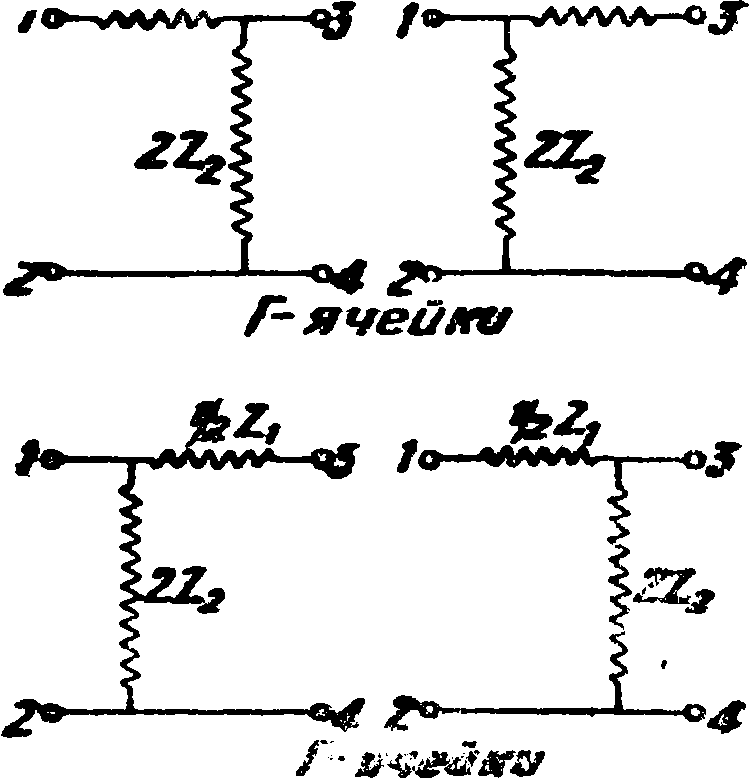
Э. ф. различаются в зависимости от 1) схемы ячейки и 2) пропускаемости токов различных частот. По виду схем ячеек в настоящее время конструируются след, системы Э. ф. (фигура 3):

1) Г-образные, 2) Т-образные, 3) П-образные,

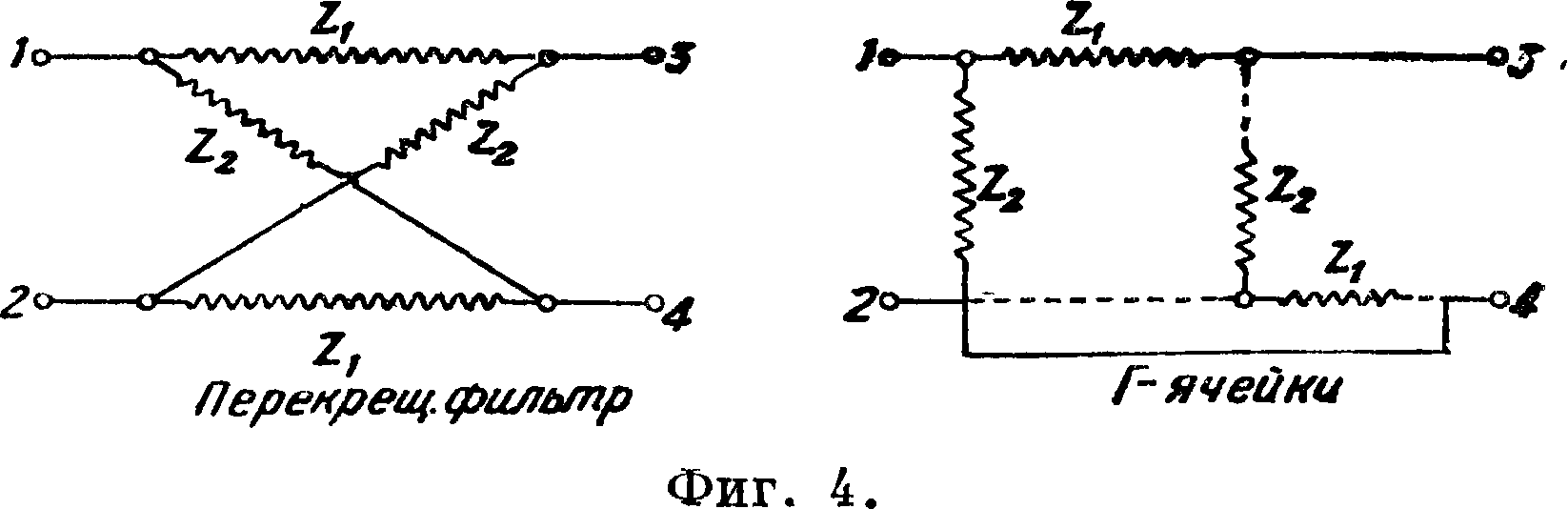
4) перекрещенные Э. ф. двух видов—Т- и П-ббразные, 5) мостиковые Т-образные. Последние применяются в тех случаях, когда величины составных элементов ячеек для других Э. ф. получаются практически неосуществимыми. Основной схемой ячейки, из которой составляются все ячейки прочих Э. ф., является Г-образная схема. На фигуре 4 показано образование Т- и П-яче-ек, а также и ячейки перекрещенного фильтра из Г-ячеек. Однако несмотря на это теоретически оказывается гораздо более рациональным изучать основные Т- и П-ячейки, тем более что и практически они наиболее распространены, тогда как ячейки Г самостоятельно практически почти не используются. С этой точки зрения ячейка Г должна рассматриваться как полуячейка. По частотной пропускаемости различаются следующие основные виды Э. ф.: 1) Э. ф., которые пропускают низкие частоты, — реактивные Э. ф.; 2) Э. ф.,

пропускающие высокие частоты, — конденсаторные Э. ф.; 3) полосные, или резонансные Э. ф., пропускающие определенную ограниченную полосу частот; 4) режек-торные Э. ф.; задерживающие определенную полосу частот. Эти виды Э. ф. могут по определенным правилам комбинироваться, образуя т. н. составные, или сложные, системы Э. ф“

Э. ф. в настоящее время нашли очень широкое и разнообразное распространение во всех областях электротехники. Наибольшее распространение они нашли в многократной телеграфии и телефонии по проводам. Здесь Э. ф. являются основой всех аппаратов. Они применяются также в этой области в телефонных трансляциях, для разделения сигналов Морзе от телефонной

/о- WW&VW* г ¹ О JT

I Ua

2о-

-04

Г- фильтр

τ-фильтр

~о₄

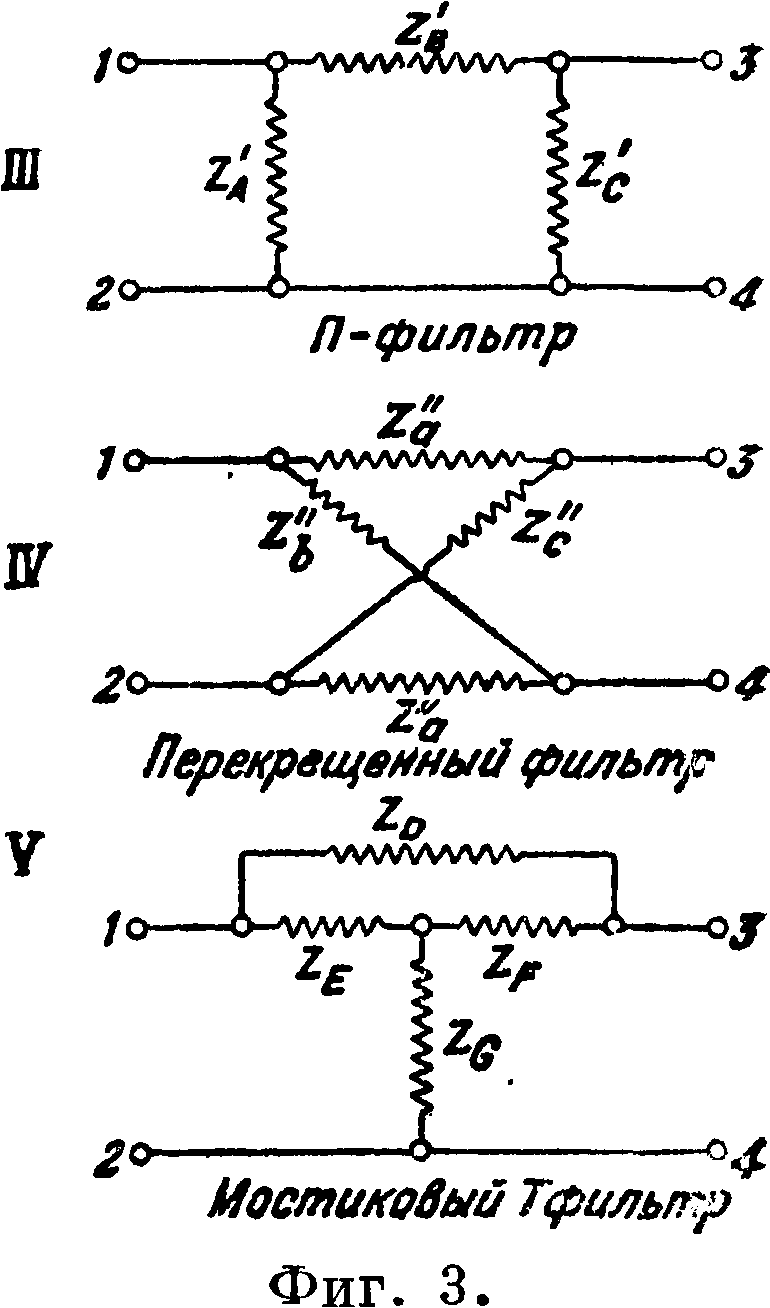
передачи и т. д. В радиотехнике применяются для связи отдельных каскадов усиления, для селекции, защиты или дросселирования отдельных цепей от токов нежелаемых частот, для коррекции искажений в радиотелефонии без несущей частоты и т. д. В измерительной технике Э. ф. позволяют разложить и анализировать сложные явления: они дают здесь настолько хорошие результаты, что часто бывает целесообразным преобразовать механические колебания в элейтрич. ток для дальнейшего их изучения с помощью Э. ф.; это относится к человеческому голосу, музыке, всевозможного рода шумам и т. д. Наконец в общей электротехнике они применяются для разделения различных токов, защиты цепей, для выявления или ликвидации гармоник. Э. ф. с успехом могут заменить дроссельные катушки, конденсаторы для защиты цепей, а также для устранения коммутационных пульсаций от машин постоянного тока и составляющих переменного тока в выпрямленном токе и т. д.

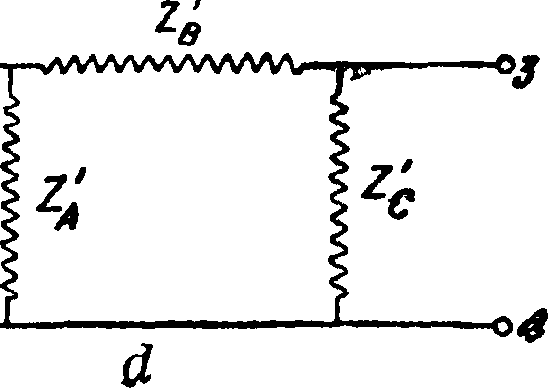
Общая теория Э. ф. Для уяснения принципов действия ячеечных Э. ф. в том виде, в котором они применяются на практике, необходимо сначала изучить основные свойства отдельных ячеек, из которых составляются Э. ф. Разбор всех различных видов ячеек Э. ф. может быть значительно упрощен, если все эти разнообразнейшие схемы электрич. фильтров свести к основной простейшей схеме или хотя бы к нескольким схемам; для этого необходимо найти законы эквивалентности различных схемЭ. ф. Найдем прежде всего условия для эквивалентного перехода в основных схемах, то есть от П-ячейки к Т-ячейке и обратно. Из теории пассивных цепей, то есть цепей, не имеющих внутреннего источника тока, известно, что для получения этих условий применительно к схемам Т- и П-ячеек нужно, чтобы сопротивления на выходе и входе ячеек оставались одними и теми же. Применяя для токов и сопротивлений обозна

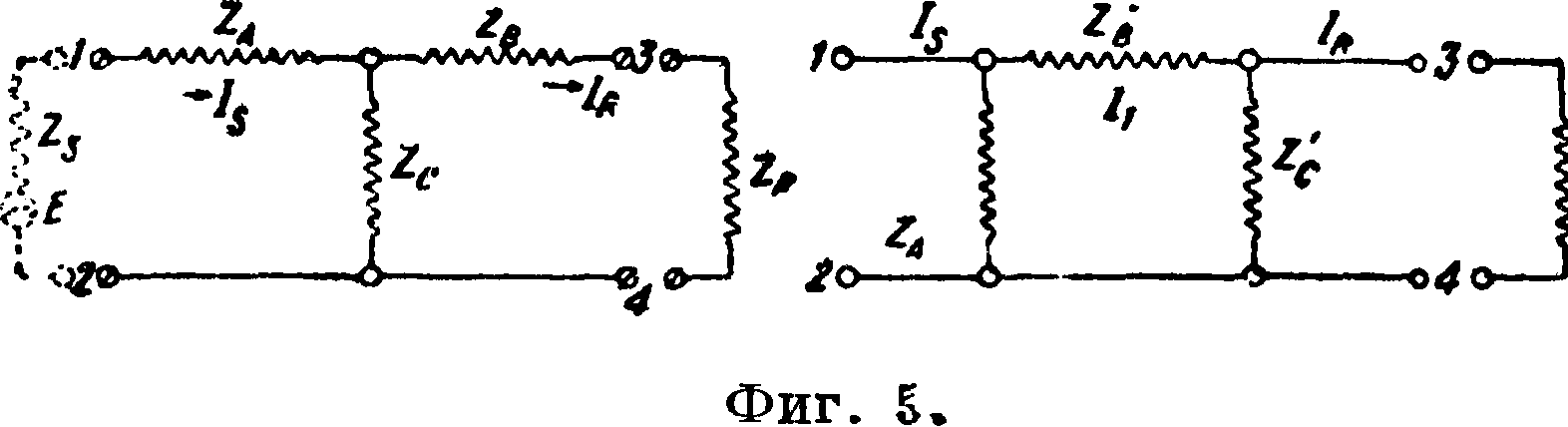
чения, данные на фигуре 5, и полагая, что к обеим схемам приложено одно и то же напряжение Е, пишем следующие ур-ия: для Т-ячейки

E ⁼ №а + Z_c) h — Z_c · Ir> /,

О=(Z_B Z_c- - Z_R) I_R — Z_CI_s f и для П-ячейки

E^ZJs-ZJ, ]

o=(Z_A + Z_B + Z’_c) 1_г — Z_Ah — Z_CI_R 1. (2)

О=(Zc + Z_R) I_R — Z_CI_X j

Из систем ур-ий (1) и (2) находим отношения E/I_s, для обеих схем: для Т-ячейки

Е_ ₌ Z_A {Z_B + Z_C) + Z_BZ_C + Z_R (Z_A + Z_C) iov Ig Z_B + Zg + Z_R

и для П-ячейки

,,

^zm^a+^zb+^z’c> + ^z’c^a + ^zb> ^{( )}

Для получения условий эквивалентности прежде всего должен быть равны правые части ур-ий (3) и (4). Затем, чтобы это новое уравнение было спра ведливо для всех значений Z_R, приравниваем коэф-ты одинаковых степеней Z_R обеих частей уравнения. После приравнивания этих коэф-тов и производства над ними ряда преобразований находим следующие условия эквивалентности: эквивалент Т для П

Za — -	zazb	λ
	za + zb + zc
Zn —	zbzc
	Za + ZB + Zc
Zn == -	zlza
6	ZA + ZB+Zc	I

эквивалент П для Т

У _ Z_AZg + Z_AZ_B + Z_BZ_C

z_A —

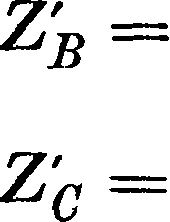
Z_AZc + Z_AZ_B + ZgZ_B

Zc

Z_AZc + Z_AZ_R -f Z_RZc Z_A

(6)

Таким же образом можно найти условия эквивалентности и для других видов ячеек фильтров. Для перекрещенного фильтра имеем: эквивалент Т

z_A=z_B=Z

г z_bz_c-zi

^С 2Z_a + Z_b + Z_f ’

эквивалент Π

у _ rj_t _ Z_a (Z_b -f- Zq) + 2ZjZ^

^A~ ^C ~ 2Z_a + Z_b + Z,

,, Z (Z_b + Z_c) + 2Z_aZ_bZ_c

^ZB- z_bz_c-z%

Для ячейки мостикового Т-фильтра имеем:

эквивалент Т

7 _ у _ Z_DZ_E

Z_A — Zj_R- _{Zi) + 2Z}^,

у _ 7

ZC + z_D + <iz_E эквивалент Π

Ζ_Α ⁼ Z_c=Ζ_Ε + 2 Z_G,

^Ζβ —

ΖρΖ_Ε (Ζ_Ε+ 2Zg) Ζ_Ε(Ζ_Ε+ %Zg) -f- ZpZg.

Для получения полной эквивалентности ячеек, имеющей физич. реальность, недостаточно только эквивалентности внешнего действия ячеек; необходимо, чтобы эквивалентные полные сопротивления, из которых состоят ячейки, имели одинаковый закон изменения с частотой, а также чтобы их фазовые углы и относительные величины были теми же самыми. Эквивалентные ячейки получаются легко, если они состоят только из емкостей или только индуктивностей. Часто для получения одинакового закона изменения с частотой на широком диапазоне отдельные полные сопротивления нужно заменять для получения эквивалентности некоторыми физически реализуемыми комбинациями их. При этом для получения положительных полных сопротивлений можно пользоваться эффектом отрицательных индуктивных емкостных и омич, сопротивлений. В качестве примера рассмотрим Т-ячейку, представляющую Э. ф. с пропусканием низких частот, у которой Z_A=Z_B (фигура 6). Ей эквивалентная П-ячейка м. б. составлена на основании следующих ур-ий:

Z_A — Z_c — Z_A+ 2 Z_G — —~ — j

y> _ Z_A у 9 K*A -r & A

Z_B - _Zc ( Z_A + LZ_C) ¹ Z_A- (Z_A + 2 Z₀)

(ZA±2Zc)Z_A

Т. о» здесь Z_A представлен полным сопротивле-

(L С

—, —I, a Z_B состоит из 2 полных сопротивлений в параллель: 2Z_Aи —2 (Z_A + 2Z_c) или 2Z_A и —2Z_A.

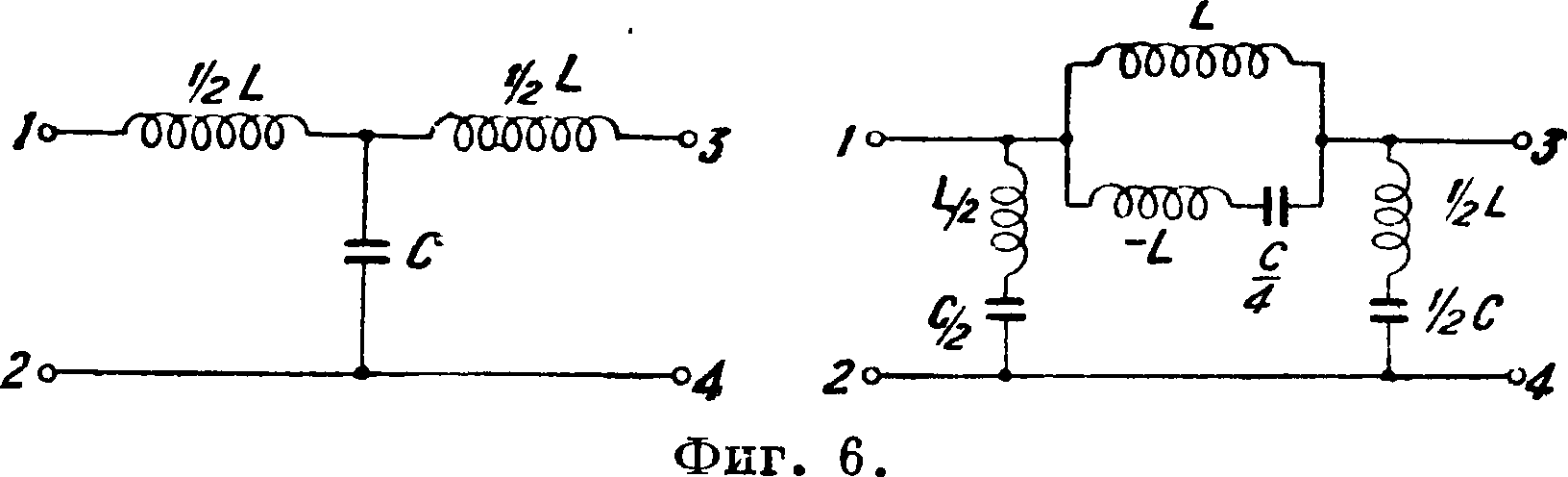
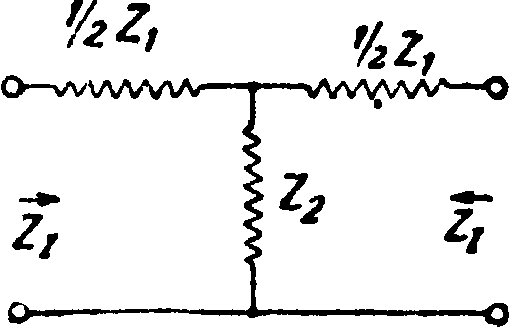
Симметричные ячейки. Все схемы ячеек, показанные на фигуре 3, называются несимметричными ячейками. В большинстве случаев практики пользуются ячейками, у которых имеется только 2 различных по величине полных сопротивления: одно в последовательном включении, другое—в параллельном. В Т-ячейке берут тогда Z_A=Z_B, в П-ячейке Z_A — Z_c. Обозначаем в таких ячейках

Z_A + ^ΖΒ — Ζ_χ, %С — ^Ζ2и

Z_A — Z_c=2Z₂ и Z_b=Z_x.

Такие ячейки носят название симметричных (фйг. 4 для Т и П). На фигуре 7 показаны симметричные перекрещенные ячейки Т и П.

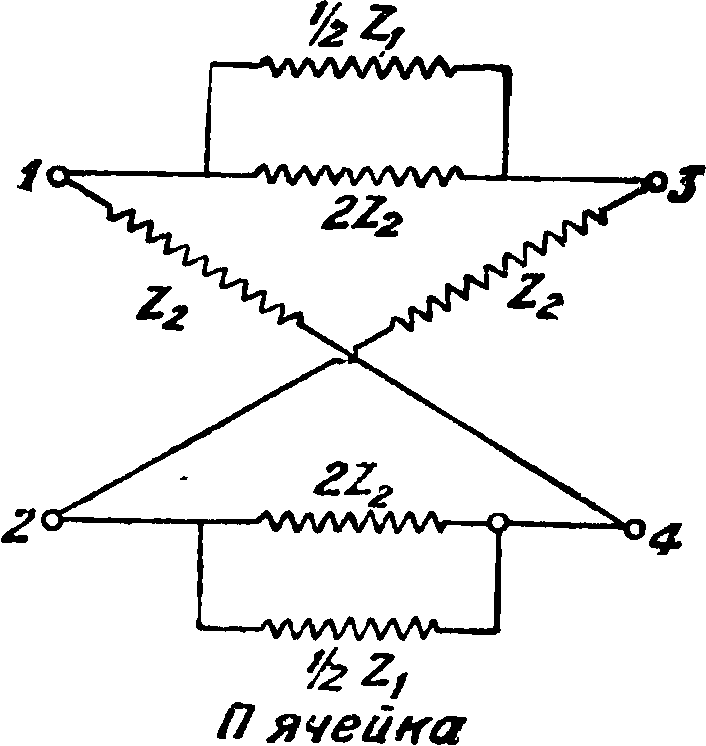
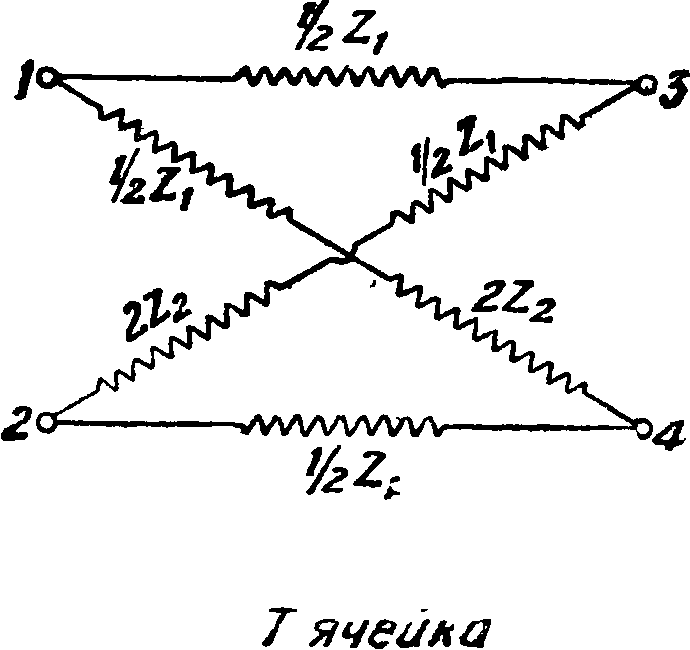
Фигура 7.

Характеристика сопротивления Э. ф. Чрезвычайно существенную роль в работе Э. ф. играют величина сопротивлений Э. ф. со стороны его входа и выхода, правильный подбор сопротивления нагрузки, на которое работает Э. ф. своим выходом, а также внутреннее рабочее сопротивление источника тока или генератора, который действует на входе Э. ф. Если посмотреть на Э. ф. со стороны входа, то его сопротивление Z,₂, получающееся между зажимами 1 ж 2 (обозначим через Z_KJ, при сопротивлении нагрузки на выходе Z_R

^Z4 ^{= Z}4 ^{= Za} + Г—~~1.· (⁷)

Z_c + Zjt

Соответственно сопротивление со стороны выхода Zg₄ на зажимах 3 и 4 (обозначим его через Z_k2) при сопротивлении источника Z_s

^ZH=Ζ*₂=Ζ_Β Η--1-—ι-, (8)

Z₍ ^ A "4 Z_s

где Z_s — сопротивление источника. Для обеспечения эффективной работы Э. ф. существует два различных принципа в выборе сопротивлений Э. ф. на входе и выходе и внешних сопротивлений нагрузки на входе и выходе. Первый принцип — повторяющихся полных сопротивлений. Для реализации этого принципа устанавливают равенство

Zjc_x ^{= Z}R “ %к₂ — Zs- (9)

Схема ячейки Т, работающей на этом принципе, показана на фигуре 8. Подставляя равенства (9) в ур-ия (7) и (8), получаем след, ур-ия, устанавливающие зависимость между величинами повторяющихся полных сопротивлений и составляющих полных сопротивлений ячейки для

^1 ⁼⁼ γ (У [Z_A + Z_B) (Z_A + Z_B + 4Z_c) +

+ Z_A- Z_B)

и для J. (10)

^zh=i (V&a + Zb) (z_A+z_B + kz₀) -1

“ z_A + Z_B)

Сопротивления Z_k и ^Zk₂

)

и называются повто-

ряющимися полными сопротивлениями.

Этот принцип имеет большое значение при составлении многоячеечных Э. ф. Второй принцип — зеркальных полных сопротивлений — заключается в том, что берется

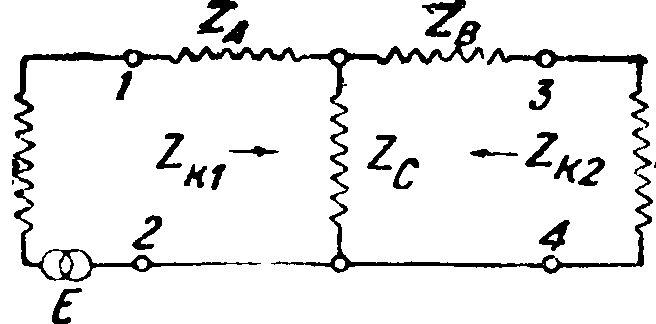
Фигура 8.

Zi_a=Z₈ И Z_R=Zg₄. (И)

В целях отличия в дальнейшем этого метода от только что разобранного обозначаем сопротивление Э. ф. на входе через Zi_lf на выходе Ζι₂; тогда сопротивление источника Z* должен быть равно Zij, а сопротивление нагрузки Ζι₂. Сопротивление Э. ф. на входе между зажимами 1 ж 2 изобразится по аналогии с уравнением (7) след, ур-ием:

7 _ -7, Z° (Zb + Zh) z4 z* + zc + zs + zh	= ZV	(12)
на выходе между зажимами
^. ZtfJbi + Zj,) 31 В+ ZC + ZA + Zh	= Ζι2.	(13)

Решая эту систему ур-ий для Z _x и Ζι₂, находим <7 _ 1Г (Z_a + Z_c) (Z_AZ_B + z_Az_t7 + Z_BZ_C) u,

^Δχ! ~ У ZF+Z~c- ⁽¹⁴>

и

^ _ 1 r z_B + Zc) <z_Az_B + z_Az_c + Z_BZ_C)

- V Zj+z^ · (¹⁵>

Следовательно Э. ф. с зеркальными полными сопротивлениями характерны тем, что у них на входе и выходе (линии АА_± и ВВ_г на фигуре 9) сопротивления в обе стороны равны. На фигуре 9 изображена схема Э. ф., построенного по этому принципу. Величины сопротивлений Э. ф. на входе и выходе, т. e. Z _x и Ζι₂, могут быть также установлены при помощи другого, очень удобного с точки зрения практики уравнения, которое дает зависимость этих сопротивлений от так называв-· мых полных сопротивлений для короткозамкнутых и разомкнутых концов Э. ф. Если измерить сопротивление Т-образной ячейки между зажимами 1—2 при разомкнутых зажимах 3—4, то это сопротивление разомкнутого конца (обозначим его через Z_oc) определится из ур-ия Z_oc — Z_A + Z_c. Сопротивления между зажимами 1—2 для замкнутых накоротко зажимов 3—4

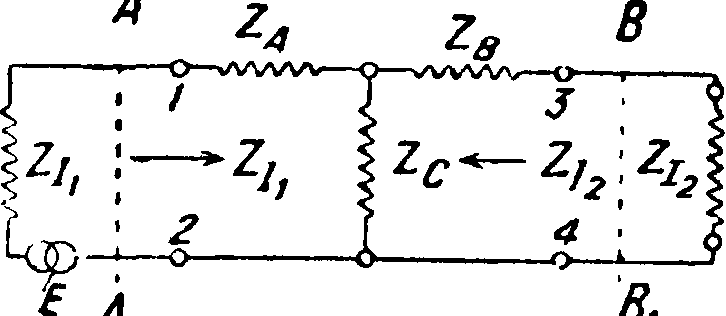
^Zsc — Z_A +

z_Bz_c

Zb + Zc

Подобным же образом найдем аналогичные сопротивления Zoc и Zsc между зажимами 3—4

для разомкнутых и замкнутых зажимов 1—2: Zoc=Ζβ + Zqг и

Zs_c — +

Za+Zc

Решая эти 4 ур-ия для Z_A, Z_B и Z_c, находим: z_G=уZo_C{ z_oc - Z_sc)=yzjz^z^), (16)

— %oc ~~~ У Zoc [Z_oc — Z_sc) =

- % - /, <¹⁷)

Z₅=Z_oe — V Z0c (Z_ot, — Z_sc) =

⁼ Z_oc ~ i Z_oc ( Zqc — Z_sc) · (16)

Подставляя ур-ия (16), (17), (18) в ур-ия (14) и (15) для Z_A, Z_B и Z_c> найдем

^Zli ⁼ Т^ЛГ, ¹⁹⁾

Z_l2=Zос Zsc · (20)

В симметричных Э. ф., то есть при равенстве Z_A=— Z_Bi повторяющиеся и зеркальные полные сопротивления становятся равными друг другу, то есть мы получаем следующее равенство:

^Zh — ^Zk-i — Zli — Z_u — Zi —

= VZ_A (Z_A + 2Z_c).

(21)

Z_k—в о л новое сопротивление Э.ф., аналогичное волновому сопротивлению длинных электрич. линий.

Распространение тока через Э.ф. Для Э.ф., работающих на базисе повторяющихся полных сопротивлений, постоянная распространения у — натуральный логарифм отношения тока на входе 1_г Э. ф. к току на выходе /₂> ^т* ^е*

У=In 4-. (22)

/₂

причем отношение — здесь соответствует потерям в Э. ф. Ток на входе Э. ф. 1_г— это тот ток, который потечет через сопротивление нагрузки, если Э. ф. удалить; ум. б. выражена в зависимости от полного сопротивления Э. ф. В самом деле, для у можно написать:

y=ln-4=In

(Ζ₄+Ζ₄)(Ζβ+ z_c+ z₄) _

Ζ _Χ + Zfc₂ EZc

Z_B + Zc +

= ln-

(22)

Для того чтобы выразить у в зависимости только от Ζ_Α, Z_B и Z_c, подставляем ур-ие (14) в (22); после ряда преобразований получаем

,._lnJ±St^₊

+ V( ^{ZA +} 2Z_c^t?-^ZC)²-ⁱ · И

Это ур-ие м. б. выражено в более удобном виде, если вспомнить, что In (a -fУ а² — 1)=Arch а,

у=Arch -^ΖΑ+ ξν + ^27с. (24)

Т. к. токи на входе и выходе Э. ф., построенного на повторяющемся базисе, остаются одними и теми же при распространении в любом направлении, то у здесь не зависит от выбранного направления. В многоячеечных Э. ф., построенных по этому принципу (фигура 10) с одинаковыми или различными постоянными распространения, отдельные ячейки оказываются соединенными с последующими по тому же принципу, что одна самостоятельная ячейка, а следовательно такой многоячеечный Э. ф. оказывается совершенно эквивалентным одной ячейке. Если постоянные распространения отдельных ячеек многоячеечного Э. ф. — у_х, у₂ и т. д., то его общая постоянная распространения равна сумме постоянных отдельных ячеек. В случае Э. ф., построенного на «зеркальном» базисе (т. к. полные сопротивления на входе и выходе его неравны), для представления о передаваемой через Э. ф. энергии необходимо уже постоянную распростране-

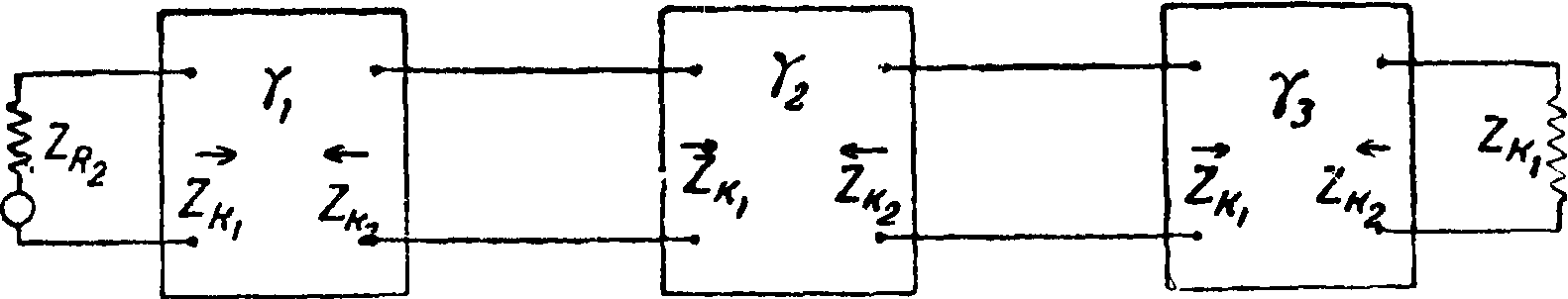
Фигура ю. ния (обозначим ее здесь через Г) выразить через ΥΑ на входе и выходе Э. ф. или ячейки. Т. о.

Г =

т^1п

ViA.

Vzh

(25)

где V₁ и 1_Х — напряжение и ток на зажимах 1—2_Уa V₂ и 1₂ на зажимах 3—4. Т. к. У_г= I_±Z_U и У г=h^z4,

Г =

±1п

2

I lZij

⁷¥ч

= 1п

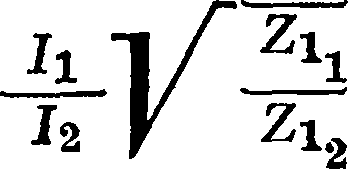
(26>

Если распространение происходит в обратном направлении, то соответственно

<²⁷>

где Г₂—ток на зажимах 3—4 Э. ф., 1[—на зажимах 1—2. Пользуясь теоремой взаимности _гможно показать, что ур-ия (26) и (27) дают одну и туже величину Г. Складывая ур-ия (26) и (27), h К

получаем 2Г=-у- · -у- или

^/,=^ΐη/4·γ* ^{28>

Т. о. постоянная распространения здесь — логарифм среднего геометрического из отношения токов входа и выхода для передачи в двух направлениях. Принцип зеркальных полных сопротивлений оказывается чрезвычайно рациональным при составлении сложных многоячеечных Э. ф.’, состоящих из целых ячеек и их половин (Г-ячеи-ки). Ячейки, соединяемые по этому принципу, м. б. совершенно непохожими друг на друга, однако Э. ф., составленный из них, будет правильно работать при условии, если зеркальные полные сопротивления в точке соединения их точно пригнаны в смысле их полного равенства. На фигуре 11 изображен многоячеечный

Фигура И.

Э. ф. с ячейками, соединенными на зеркальном базисе. Общая постоянная распространения такого Э. ф. равна также сумме Г₁₉ Г₂, Г₃ отдельных ячеек. Постоянные распространения Г_иГ₂, — ^в общем комплексные величины: Г_г =

= α_χ + ]βι Г2= а₂+/^2 и т. д. Γ=α+]β, где а— постоянная поглощения Э. ф., β — фазовая постоянная, причем α= + а₂ +. и /3=+

-р /?₂ -Р. В симметричных ячейках у=Г, так как отношение Z_Ii/Zj₂, входя в ур-ие (26), для Г становится равным 1. Действительные и мнимые части постоянной распространения тоже становятся равными.

Отражения в Э. ф. Основное преимущество Э. ф., построенных по принципу зеркальных и повторяющихся полных сопротивлений, заключается в том, что в них полные сопротивления на входе и выходе находятся в определенных соотношениях с составляющими полными сопротивлениями Э. ф. Отклонения в соотношениях полных сопротивлений приводят к снижению эффекта, даваемого Э. ф. на выходе. Однако получить сохранение этих соотношений на широком диапазоне частот не удается, так как Z_k (уравнение 21) изменяется с частотой и по характеру и по величине. Поэтому обычно величины полных сопротивлений нагрузки выбирают для какой-нибудь одной частоты (или для ряда различных частот) в пределах спектра, пропускаемого Э. ф. Пели сопротивление Z_kна выходе не равно сопротивлению Э. ф. Z_s, то сила тока на выходе м. б. значительно снижена, т. к. часть тока отражается от конца подобно тому, как это бывает в линиях. Вспомнив уравнение (26), можно установить следующее отношение тока /₂ на выходе при выключенном Э. ф.

^когда /₂=_z ^ j и 1₂ при включенном идеальном Э. ф. с Г=0 и при Ζ_κφΖ_α

h ί/* 4 z₈z_r

r₂ ~~ V z_s + z_R

(29)

Это соотношение называется фактором отражения полных сопротивлений Z₈ и Z_R Э. ф. Оно называется так потому, что неравенство полных сопротивлений Z₈ и Z_R создает здесь явления отражения и в случае систем, обладающих малыми искажениями, может привести к резко выраженным отражениям. Величина, обратная фактору отражения, является мерой эффективности передачи в месте соединения Z₈ и Z_R без Э. ф. по сравнению с передачей, получающейся при включении идеального Э. ф. с нулевой постоянной распространения. Эта величина соответствует обычно потерям при передаче. Эти потери называются потерями от отражений. Во многих случаях, в частности в рассматриваемых Э. ф., однако она соответствует в действительности увеличению токов. Потери от отражений N между какими-либо двумя полными сопротивлениями, выраженные в децибелах,

N=20 lg

к

h

= 20 lg

_Z_±+ZR_ У iZ_s + Zjt

(30)

При обычном Э. ф., имеющем Гф 0, неравенство зеркальных полных сопротивлений вызовет сложные явления. Для определения тока на выходе при любом Э. ф., соединяющем Z_s и Z^, поступают след, обр.: определяют 1) ток на выходе при равенстве сопротивлений на концах Э. ф. и 2) эффект, обязанный изменению сопротивления нагрузки от величины Z_s к величине Ζχ. Ток на входе Э. ф., построенного на «зеркальном базисе»,

I

^Ао 2Ζι_χ »

ток на выходе

- V

*-Z_s

V kz₄z_s

(31)

: εΛ (32)

Предположим теперь, что сопротивление нагруз-ки изменилось с Z_s до Z_R. Т. к. эдс, действу ющая на выходе, равна 2/₂ Z_si то при новых условиях ток на выходе

2Z_S

^гч=* < ³³>

Изменившееся сопротивление на выходе на величину Z_R— Z₃ создает на выходе дополнительную эдс

*ί=-Ιί₉{Ζχ-Ζ). (34)

Эта эдс создает на входе ток

* ε-Γ =

егЛ (35)

Ч ^{V 4Zl}i^Zs

Подставляя ур-ия (33) в (34) и (34) и (32) в (35), получаем

Δ7,=- г гд-Zs

^{18 2}° z_R + z_s

Zr-

2Z,

к

V 4Ζι Z«

ε-*Γ.

: ε~^Γ =

(36)

Zr + Z_s

Для полного тока на входе имеем

-л,+»л„«-)·(«!

Сопротивление на входе Э. ф., когда сопротивление нагрузки на другом конце Э. ф. не равно «зеркальному полному сопротивлению», м. б. представлено в следующем виде:

Е 1. _

h_a *

JL-7

Zr — z$ Zr -f Z_s

p-2 Г ¹

1

Z_R-

-2Г

(38)

откуда

^{Z = Z}h

Zr + Z_s2

1 —

1 +-

Zr Z_sZr + Z_sZr - Z_s

= Ζ_λ

Zr + Z_s

1 Zr — Z_s

1 —

Выражение

Zr + Z_s

ZR-Zg

-гг I	1
-bГ
-гг	(39)
	(39)

ZR + Zg

называется коэф-том отражения; обозначим его через ρ_χ, тогда

Ζι =

^J2

откуда

“2г -

„ 1 + Zh 1 _ ’	(40)
Ζΐ·--Ζΐι =е. Zh+Zh	(40)

_Ql8-

ρ — коэф. отражения на входе при коэфициен-те на выходе ρ_χ. Если сопротивления нагрузки на обоих концах не соответствуют зеркальным полным сопротивлениям, то явления еще больше усложняются. Отношение токов на выходе при Э. ф. и без него в этом случае ф-=х · eiet^trr<r, (И)

где к соответственно ур-ию (29) -

VTz^Zr

величина, обратная фактору отражения, обязанного неравенству Z_s. и Z_R для тока /₂; о_г =

= ^ ~φ~Ζι — Ф^актоР отражения благодаря нера-

У 4Zi?Zi

венству Z_s и Z₄ и ρ₂=_Zj? + ζ_χ ~ Ф^актоР отражения благодаря неравенству Z_R и Ζ_ΐ2; ε“^Γ выражает эффект постоянного затухания и фазовой постоянной Э. ф. Наконец σ — фактор взаимодействия, обязанный повторным отражениям, показывающий, что отношение токов при не-выверенном Э. ф. зависит не только от простых по эффекту факторов единичного отражения и постоянной распространения, но также и от повторных отражений от концов Э. ф. в более сложной форме:

-ΚΙ ¹⁴²¹

σ играет второстепенную роль и может стать значительным только на частотах среза, на других же частотах σ обычно незначительно. Отношению токов уравнения (41) соответствуют общие потери, представляемые суммой индивидуальных потерь, соответствующих различным факторам. Общие потери в децибелах выражаются суммой

£= — 20 1g_2O(A)+201g_lo(4-_i) +

, + 20 ]g₁₀ (γ) + а + 20 )g₁₀ j.

Общее изменение фазы выражается суммой фазовых углов опаздывания тока, соответственно слагаемым потерь. в=+ углу к — углу Л_х - углу к₂ + β +

+ углу σ.

Условия для обеспечения работы Э. ф. Идеальный Э. ф. характеризуется следующими данными: 1) Постоянная затухания в полосе пропускаемости Э. ф. должна быть равна нулю: энергия не должна расходоваться внутри Э. ф. 2) Сопротивления нагрузки должен быть в "этой полосе активными сопротивлениями и не должны зависеть от частоты. 3) В поглощаемых полосах частот постоянная затухания должен быть по возможности наибольшей, сопротивления нагрузки должен быть или очень высокими или очень низкими для того, чтобы они вызывали большие потери от отражений на входе и выходе Э. ф., но не были причиной увеличения тока от отражений. Конечно ни одно из этих условий не м. б. полностью практически реализовано. Однако эти положения в стремлении приблизиться практически к данньпм идеального Э. ф. приводят к следующим требованиям в отношении конструирования действительных Э. ф.: 1) Э. ф. должны состоять исключительно из реактивных сопротивлений. 2) Зеркальные полные сопротивления, образуемые реактивными сопротивлениями Э. ф., должны быть или действительны- ми величинами (чисто активными сопротивлениями) или же мцимыми количествами (чисто реактивными сопротивлениями): а) если зеркальное полное сопротивление есть активное сопротивление, Э. ф. затухания не имеет, а потому свободно пропускает токи соответственных частот, при которых это условие выполняется; б) если зеркальное полное сопротивление — реактивное сопротивление, Э. ф. имеет большое затухание и не пропускает токи (не имеет «прозрачности»). Реактивные сопротивления не способны поглощать энергию, поэтому они, запасая энергию в течение одного полупериода тока, в течение другого полупериода отдают ее обратно источнику, почему Э. ф. не пропускает токи к приемнику. Зеркальные полные сопротивления любого Э. ф. согласно уравнению (20) м. б. опреде лены как среднее геометрическое из Z_oc и Z_sc. Если Z_oc и Z_cs — чисто реактивные сопротивления, то есть Х_ос и Х_ЬС9 каковыми они и должен быть в Э. ф., составленных из реактивных сопротивлений, зеркальные полные сопротивления Z₁ могут иметь три возможные величины в зависимости от знака реактивных сопротивлений. 1) Если Z_oc и Z_scпротивоположны по знакам,

з_х=VWJxJWJxj=(43)

2) и 3) Если Z_oc и Z_bC оба положительные или оба отрицательные,

^ - V(±7*J (± jx₈c)=± ί^χι- (“)

Подобным же образом Ζ также м. б. равным или R[ или i jX. Если Z^fx и Z_x— оба реактивные сопротивления, они м. б. противоположными по знаку. Зависимость затухания Э. ф. от характера зеркальных полных сопротивлений м. б. показана из следующих уже известных нам ур-ий: коэф. отражения (уравнение 39) Э. ф. при условии короткого замыкания его, то есть при Z_R=0, ρ равен —1; при размыкании его, то есть при Z_R=со, q=1. Если теперь действительное сопротивление на входе между зажимами 1 vi 2 равно Z_8C (ур-ие 40), коэф. отражения на входе

z;,+zz,	(45)
Если же оно Z0C9 то
Iм=(1) ε-*Γ-, %ОС + Zi 7	(46)

Из ур-ий (45) и (46) видно, что если Z_x—реактивное сопротивление (Z_sc и Z_oc имеют тот же знак), коэф. отражения на входе не м. б. равен 1 для конечных значений Z_sc> Z_oc и Z_1}откуда

I _ε-2Γ I — β-2_α <1 _и α > 0. (47)

Э. φ. прозрачности не имеет. Но если Ζ_χ чисто омич, сопротивление, коэф. отражения на входе должен иметь величину, равную единице, для всех конечных значений Z_8C9 Ζ_0ΰ и Ζ_χ. При этих условиях

ε~²Γ=e^-2а. ε~²β=1ε~²β и α= 0. (48)

Э. ф. дает пропускаемость при отсутствии затухания. Здесь следует отметить, что когда Э. ф. имеет затухание, коэф-ты отражения на входе и выходе из"ур-ий (45) и (46) имеют числовые значения. Т. о. для Г-ячейки фазовая постоянная β=± ηπ или

/»=±т“, (49)

где п — целое число; для Т- и Г-ячеек симметричного ряда

β=i -γ ⁷¹ — i ¹⁷¹⁷¹ > (50)

где п — уже четное число. Эти ур-ия конечно не обозначают, что фазовая постоянная в полосе непрозрачности обязательно не зависит от частоты, но они показывают, что если она изменяется, то это происходит скачками на величину целых чисел квадрантов или их половину.

Пограничные частоты пропускаемости и поглощение Э. ф. в зависимости от соотношения Z_x и Z₂, из которых состоит Э. ф., могут быть определены по соотношению Z₀JZ_S0. Для симметричной Т-ячейки, для обоих

концов	ZOS=-γΖ 1 + ^2,	(51)
	1 ΎΖιΖ2 Ζ„= 8 Ζ,+ * γΖχ + Ζ,	(52)

Т. Э. Доп. га.

35

откуда

_(*+¥)·

Zoe ₌ (Zl/2 + Zg)» _

Z$£ ZJ, 4 + ΖχΖ₂ 4 i 4Z₂Ζχ

(53)

(54)

Нетрудно убедиться, что для симметричной П-ячей-ки ZocIZsc получает то же выражение, что и для Т-ячейки (ур-ие 53). Для Г-ячейки

Zoe _ л i 4Z₂

Ζ«?“ Ζχ

для обоих ее концов. Отношение Z_0C/Z_8C для всех видов Э. ф. положительно или отрицательно [ср. ур-ия (43) и (44)] в зависимости от того,

положительно 1 + или отрицательно. Т. о. 4Z₂ ¹

выражение “,

1 4- служит критерием для оп-

ре деления пропускаемости Э. ф. Пограничные частоты между зонами пропускаемости и затухания Э. ф., называемые срезываемыми частотами, или частотами среза, имеют место, когда

1 +

или когда 1 +

4Z₂

= 0 или

Zi

4Z₂

-

(55)

Ζχ

= со (при условии, что Z₁ или знак при этой частоте), откуда

Z₂ изменяет Ζχ=0, но

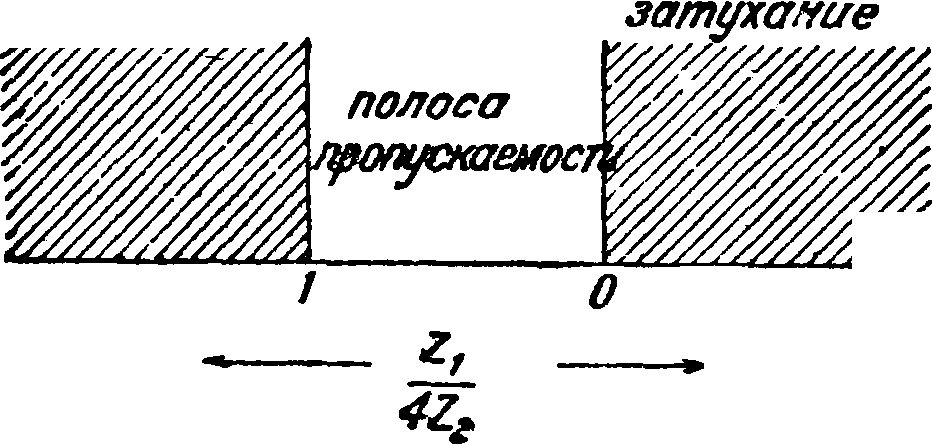
Z₂ ф 0 или Z₂=00, Ζ,φ оо. Следовательно в пропускаемой зоне

0>

J3

4 z₂

>

1,

в зоне затухания ^ > 0 или

< - 1.

Ζχ

4Ζ₂

(56)

(57)

(58)

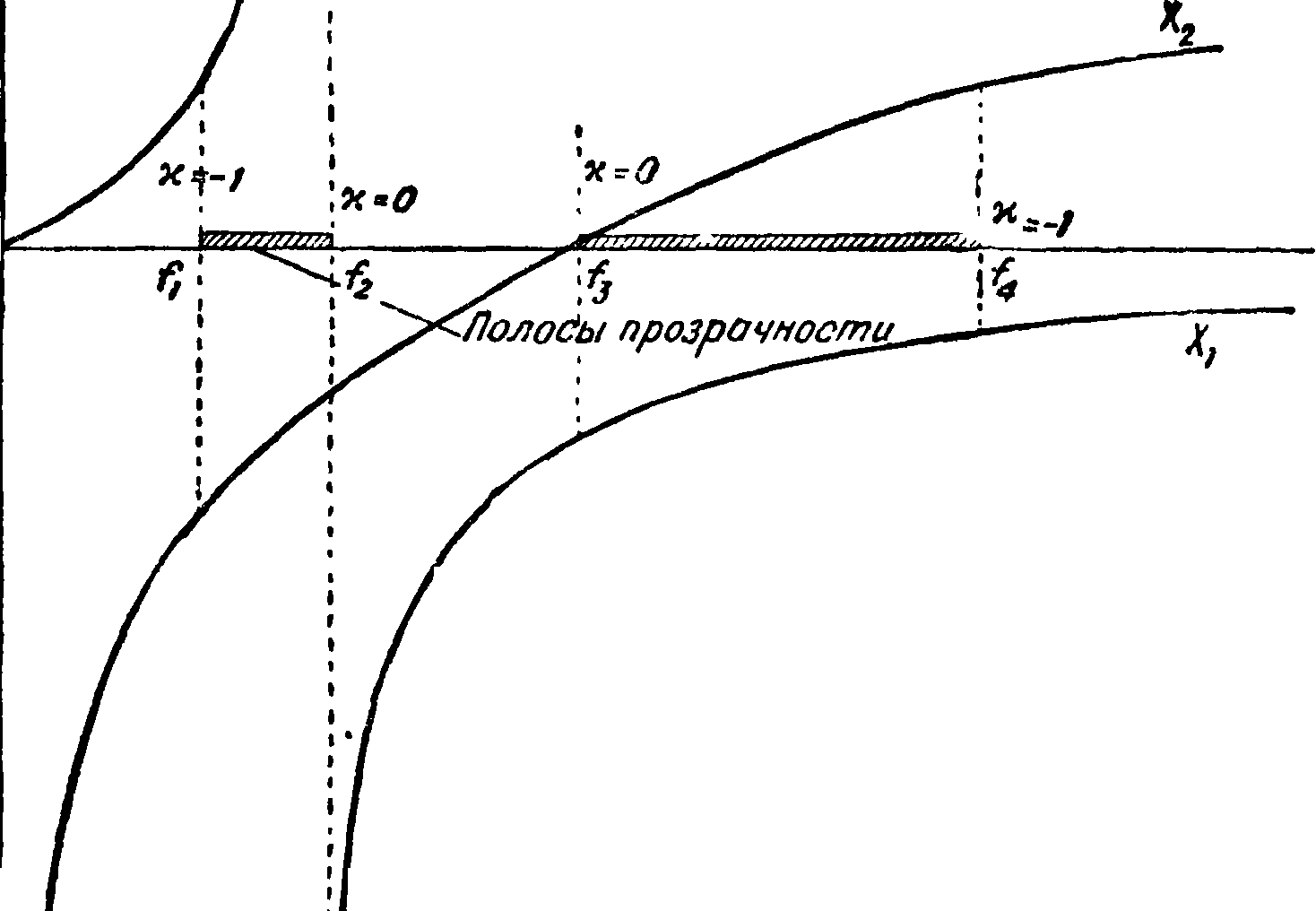
Эти результаты в схематич. форме показаны на фигуре 12.

Зеркальное полное сопротивление для симметричной Т-ячейки определится из уравнения (19), если для Z_oc и Z_sc подставить выражения из ур-ий (51) и (52):

Z₁=y^rZ₁Z₂ (l + /^). (59)

Таким же образом для П-ячейки найдем

ΖιΖ₂

+

Ζχ 4 Za

(60)

затухание

Для Г-ячейки со стороны входа зеркальное полное сопротивление —Zj, со стороны выхода —

Ζ_Γ На фигуре 13 показаны Э. ф., составленные из различных симметричных Ш ячеек, работающих на зеркальном базисе. Иногда бывает удобно пользоваться Фигура 12. вместо зеркальных полных сопротивлений соответствующими им зеркальными полными проводимостями Yj и Yj, выраженными в зависимости от полных проводимостей последовательной Y_x и параллельной Υ₂, образующих ячейки Э. ф.:

γ ₌ _L

¹ Zj;

Υι Υ₂

+

ζ₂

4Υχ

1

Vw (· + «)

(61)

(62)

Ζ₁ и У_г называются зеркальными полными сопротивлениями и проводимостями в середине последовательных полных сопротивлений Э. ф.,

I Т-ячейка

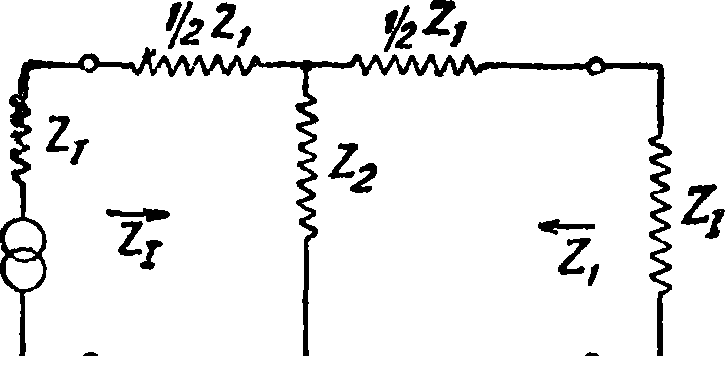
II Г-полу ячейка

2Z₂

	i
τ% т ^	1-ΛΛΛΛΛΛΛΛ— l·—^λλλ/vww— [ ^ LjL-

$

- i^z

*7 i

III П-ячейка

Фигура 13.

IV Г-полуячейка паправл. распространения обратное

Ζι, и проводимость Yj то же в середине параллельных полных сопротивлений Э. ф. Из приведенных уравнений вытекают следующие важные положения:

^=^=¹ + + ⁽⁶³>

(64)

(65)

(66)

V Z₁z₂=|/z₁ Zi,

PCX=ужж

V ΖχΖ₂

VYiY₂.

Υι

V ΖχΖ₂

У Υ1Υ2

Условие пропускаемости Э. ф., определяемое ур-ием (57), м. б. удовлетворено одним из 4 способов, показанных в таблице 1.

Таблица 1.—Условия пропускаемости Э. ф.

Ζλ_ 4 Ζ2	Ζχ	Ζ2	Зеркальные полные сопротивления
			Zi	zi
0	0	конечное	0	0
0	конечное	сю	со	00
0	0	оо	конечное	конечное
-1	конечное	конечное	0	оо

В поглощаемых участках Zj и Z — чистые реактивные сопротивления, принимающие первое знак Ζχ, второе знак Ζ₂; Ζ_τ в поглощаемой полосе — отрицательное реактивное сопротивление, тогда как Zj выше пропускаемых частот—реактивное сопротивление положительное, ниже — отрицательное. Для определения постоянной распространения, подставляя в ур-ие (45) выражение из ур-ия (19), получаем ур-ие

-2 Г

1

4- l/"^Z€£

^ V z_ac

(67)

Это ур-ие м. б. представлено также в гиперболической форме

(68)

Г — Arcth λί~,

г Zap

так как

У1-

» Zqc

1 — ε"

г2Г

εΓ-_ε-Γ

1 +

+ «

-г

th Λ

сти. T. о. полось1 частот, в которой затухание везде равно 0, не существует. Э. ф. всегда ослабляет ток, даже и в полосе прозрачности, что впрочем очевидно и a priori, так как сопротивление катушек поглощает энергию. Эффект сопротивлений в Э. ф. выражается в том, что они дают затухание там, где ток должен проходить свободно и уменьшают затухание там, где оно должен быть по возможности наибольшим. Постоянная затухания и фазовая постоянная при наличии омич, сопротивлений в Э. ф. могут быть определены след. обр. На основе ур-ия (75) имеем

|Z,/4Z_a|=VTp+v².

Далее, если предположить фазовый угол

IZ./4ZJ равным а?, имеем cos φ=—^U — или ^{1 Г} Vu 2 + V2

Y V² + F² cos φ — U.

Подставляя ур-ие (75) в (72), имеем:

Г=Arch (1 + 2С7 + /2F). ^ (79)

На основании ур-ия

Arch (А + jB)=Arch ~ [YВ² + (1 + 2J² +

+ Υ& + (1 _ А)² +

+ arccos -i- [/В*+ (1+А)² — у В² + (1 — А)Ц имеем для Г:

Г= Arch у [У4F² + (2 + 2t7)²+jAF² + (2 — 2U)·] +

+ arccos у- [ylV* + (2 + 2ΐγ+ΥF²+(2-2 t/)²].

Если через κ обозначить абсолютное значение Ζ-,/4 Ζο, тогда

Г=Arth у ++=arcsin у · (74)

Т. о. постоянная распространения для Г-ячейки в 2 раза меньше, чем для целой ячейки Т и П.

Влияние сопротивлений на действие Э. ф. До сих пор мы предполагали, что элементы, составляющие Э. ф., представляют собой реактивные сопротивления при отсутствии омич, сопротивления. Практически такой Э. ф. реализовать конечно нельзя. Обычно и катушки и конденсаторы, применяемые в Э. ф., особенно первые, обладают омич, сопротивлением. В этом случае Z_x и Z₂ — уже не только чисто мнимые количества, они -имеют и действительную часть. Следовательно ZJkZ^ больше уже не действительно, а состоит из действительной части U и мнимой части jV.

k-^u + i^v· ‘⁷⁵>

Ур-ие (72) получает вид:

ch Г =(1 + 217)+/2 Г. (76)

Т. к. кроме того ch Г=ch (а + //?), то мы можем написать

ch a cos β + ch a sin β=(1+2 Ζ7) + 2F, откуда, отделяя действительные и мнимые части, имеем 2 равенства

ch a cos β=1 + 2 U Ί sh α sin β=2V J ⁽⁷⁷⁾

ИЛИ

th α · tg /?=· (78)

Это уравнение показывает совершенно наглядно, что а никогда не м. б. равно 0 за исключением отдельных частот, когда tg β равно бесконечно-

*=|Ζ₂/4Ζ₂| =Υυ*+ F² и и=У V² + V² cos φ=κ COS φ.

Подставляя эти выражения в ур-ие для Г и. преобразуя его, имеем окончательно:

Г — Arch У {κ —I)² + 4 κ cos² φ/2 + κ + a

+ cos"¹ У (κ — l)² 4 + κ cos² φ 2 — κ. (80)

На фигуре 14 и 15 показаны кривые для а и β в зависимости от Z_t/4Z₂ для различных значений угла φ. Для пользования этими кривыми

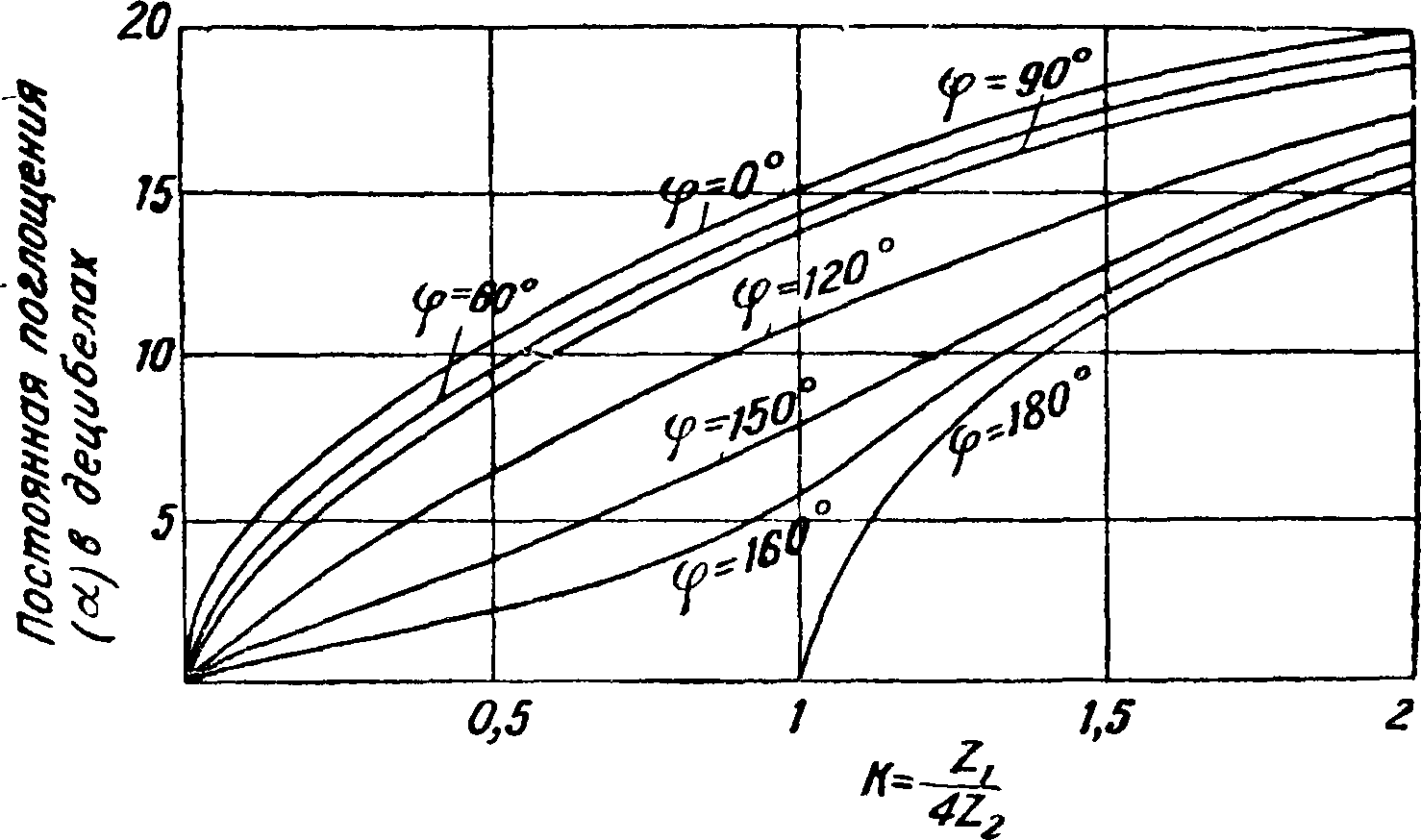
Фигура 14.

необходимо выразить Ζ₁/4Ζ₂ в полярных координатах. Модуль и аргумент дадут тогда соответственные значения κ и д?, например: если Z_xlkZ₂— действительная и положительная величина, то κ — Z_xlkZ₂ и φ — 0°. Если Z_xjkZ₂—действительная и отрицательная величина, κ=Ζ_χβ*Ζ₂ и φ=180°; если Ζ_ΧΙ^Ζ₂ комплексно, тогда

Пз ур-ия (19)

‘ + F:

-Tin-

1

-V:

_ 1 l_n Zor ~b F Z_nrZ_sc (p.Q

2 ¹¹¹ 7 _ 1Г₇~ 7 ~ * ^

Подставляя в ур-ие (68) ур-ие (53), получим

/z lk + z_xz_%

Г Arth у _(Zim_H._Z2)2для несимметричных Э. ф.,

Г_ Arfhl/" ^{ZaZb + Z}B^Zc + ^ZcZa

~ У (Z_A + Z_C) (Z_B + Zc)

при симметричных Э. ф. Г=у. Полагая

1 + Zj/2Z₂=х,

= Arch х

Г=Arth

ch г=*=а+^г+_е-^г],

.г — 1 2

4-С-* + *-^г)

(70)

(71)

(72)

]/-7-=т(^бГ/2-^^г/2)=^^².

откуда

Г=2Arsh j/"Z_t/4Zj. (73)

T. о. мы снова устанавливаем положение, что работа Э. ф. зависит от отношения Z,/4Z₂. Для Г-ячейки, представляющей полуячейки Т и П, аналогичным образом из ур-ия (68) найдем, что его можно выразить в виде г0 и κ=г и φ — Θ. На фигуре 14 две крайние кривые для φ — 0° и 180° — идентичны, но кривая для φ=180° смещена вдоль оси 2^/4 Ζ₂ на величину 1. Для больших величин |Zj^ZJ эти кривые сливаются; все кривые с промежуточными величинами углов лежат между ними, таким образом затухание для больших величин I Zj/4Z₂1 не зависит от фазового угла Z₁/^Z₂. Вблизи Zj/4Z₂=1, которая соответствует одной из частот среза, относительно малые изменения углов Z_t или Z₂вызывают большие изменения в затухании, а также в фазе (фигура 15). Однако здесь Z_t и Z₂обычно индивидуально не большие и не малые величины, почему мало эффективное сопротивление элементов в электрическом фильтре, состоящем по преимуществу из реактивных сопротивлений, вызывает малые изменения в φ тогда как вблизи |Ζ₁/4Ζ₂|=0 другие условия для ча

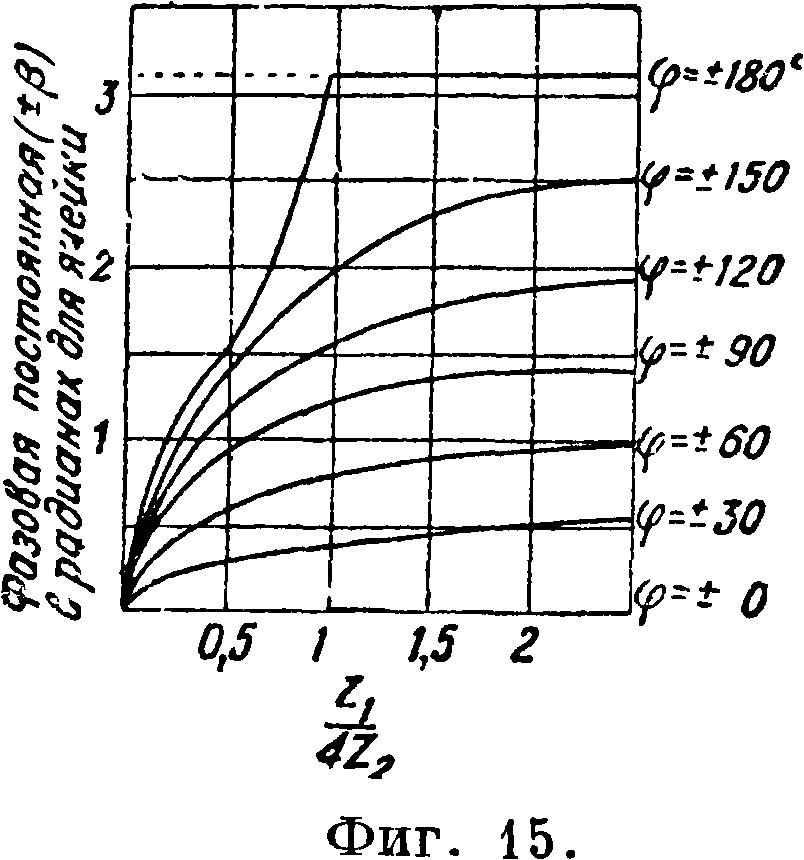
стот среза: или Ζ_χ=0 или Ζ₂=со (табл. 1). Поэтому сопротивление элементов может вызвать большие изменения в φ. Так. обр. для обеих частот среза сопротивление в реактивных элементах вызывает приблизительно равные изменения в затухании и в фазе. Для кривой с φ —=180° β может иметь в полосе прозрачности любой угол от — π до + π радиан, в полосе затухания β=0 или ± π у оставаясь постоянным, если Zi/4Z₂ не изменяет знака. Для больших Z_t/4Z₂ β становится равным φ, если они выражены в тех же единицах, то есть β=φ/π.

Полные потери в Э. ф. Пользуясь ур-ием (71), а также ур-иями (14) и (15), мы можем вывести общее ур-ие для полных потерь в Э. ф. с учетом отражений при неправильном подборе сопротивления нагрузки. Из этих ур-ий мы определяем следующие зависимости для несимметричных Э. ф.:

Ζα=Z_hjth Г - j/Z^/sh г Z_B=Zi₂/thr-l/Z^₂/shr

z_c=y^z^jshr.

(81)

Фигура 16.

Для Э. ф. (фигура 5) по законам Киргхофа можно показать, что ток т ___________^EZc_____ (82

(Z^-f-Z^) {Zr- -Zc)- ~Zr {Z_A -Zc)- -ZRZcA_rZsZR

Подставляя в это ур-ие выражения для Z_Ai Z_Bи Z_r из (81) имеем

Е V ΖΪΤΪ7

^R (Zi^, + zsza Sh Г + (ζ_τιζ_κ + Z_hZs) ch Г

T. К.

M’=4(_в^Г-_в-Ч=4<Г^Г(в“^Г-1) ch Г=е-^г(е“^г +1),

TO

J ___Д ΤΛζ^ζI₂·^ ₌

^Л (Ζϊ,Ζί,+ΖίΖΛ) (e^-D+fZ^Zfi+Z^Zs) («*^г+1)

_ E Zg+Z_J? |/~ 47^2,5· jAz^Zg __r

Zs+Zr V bZgZR Ζγ_χ + Zs Ζγ₂+ Zr

’ Ζχ₂ Zr Z_U-Z s — 2~T~‘ ^(41,)

Zj₂ + Zr Zj_i -}- Zs

Это ур-ие соответствует ур-ию (41), смысл которого был объяснен выше.

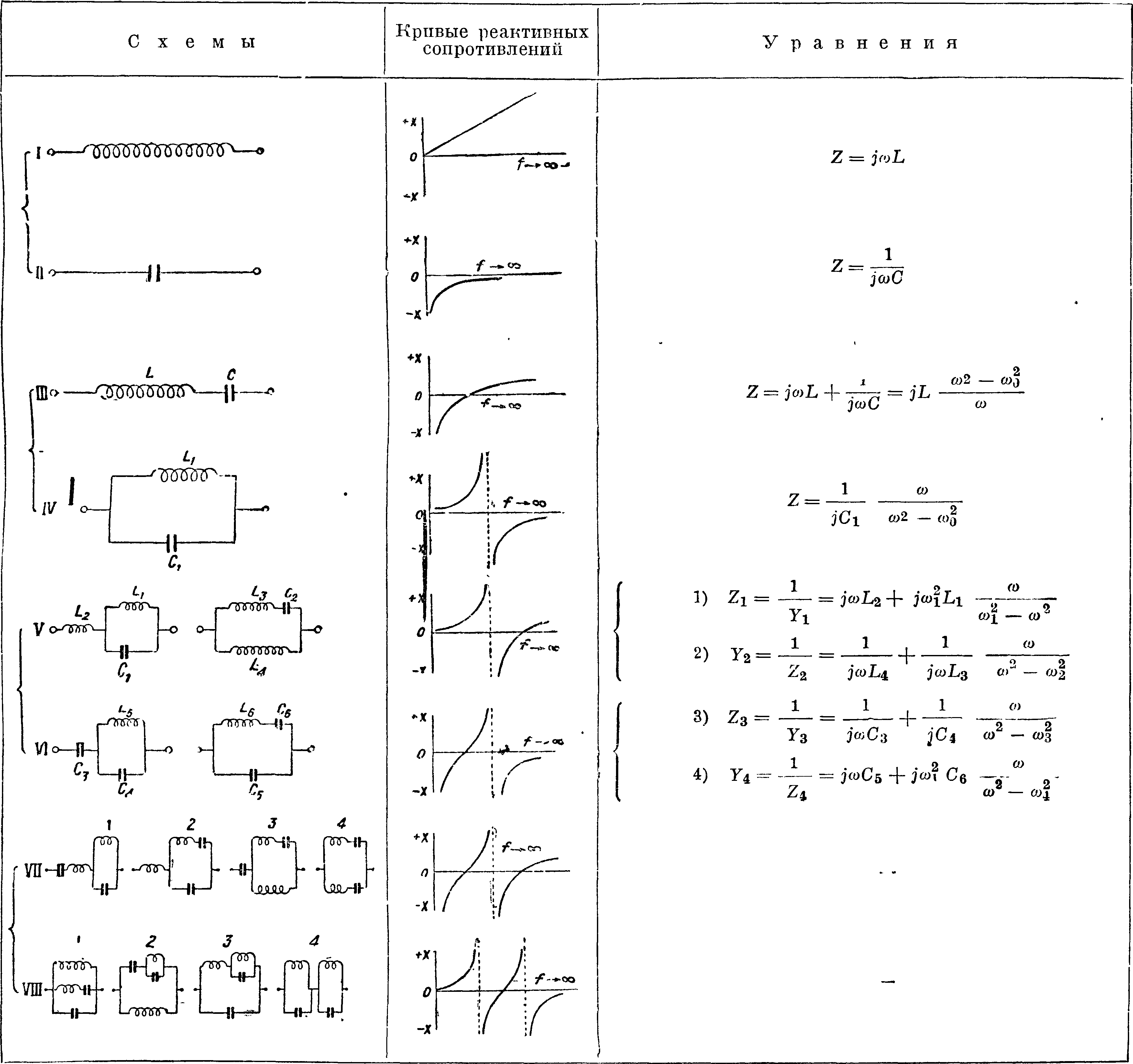
Виды реактивных сопротивлений, применяемых в Э. ф. В фильтрах, используемых для практических целей в качестве полных сопротивлений Z_x последовательных ветвей и Z₂ параллельных ветвей, находят применение чрезвычайно разнообразные виды реактивных сопротивлений. Число этих видов почти неограниченно, однако практически используются реактивные сопротивления с числом элементов не более 4—5. Значительное уменьшение числа элементов достигается применением многоячеечных Э. ф., составленных из различных видов простых ячеек. Наиболее употребительные виды двухполюсных схем реактивных сопротивлений, применяемых при конструировании Э. ф., показаны на фигуре 16. Все схемы реактивных сопротивлений распределены по па-

ЛЬ

-^/ТШЯЯГ—<

рам, отмеченным скобками. Эти пары представляют потенциально обратные реактивные схемы, то есть такие, у которых 1) полное сопротивление Z одной изменяется с частотою так же, как реактивная проводимость Y, и 2) произведения полных сопротивлений или реактивных проводимостей обоих дают постоянные величины. На фигуре _J__{_}

16 в правой части показаны кривые ^Фиг* ^17а*

изменения реактивных сопротивлений этих схем с частотой, а также характеризующие их уравнения для Z. Если одну из этих схем применить в последовательных ветвях, а другую — в параллельных, то можно соста-, вить ячейки любых ви-£** дов. При некоторых час-

£=nktc тотах отношение Zj/4Z_a! ^{J s} этих схем будет прини

мать величины между 0 и —1. Токи этих частот будут пропускаться Э. ф., токи же других частот будут или сильно ослаблены или совершенно не пройдут через Э. ф. Определение по-I >| лос прозрачности Э. ф. с этими схемами часто лучше всего по-

Фигура 176. лучается с помощью кривых ре активных сопротивлений для этих схем, показанных на фигуре 16. В качестве примера на фигуре 17а и 176 показаны кривые реактивных сопротивлений

Таблица 2.—Пропускаемые полосы.

		Zi последовательных ветвей
Z2 параллельных ветвей		1	2	3	4	5	6
	1	нет	в. ч. К-тип	р. п.	в. ч. М из 1,2	р. п.	в. ч. р. п.
	2	н. ч. К-тип	нет	р. п.	н. ч. М из 1,2	н. ч. р. п.	р. п.
	3	н. ч. М из 1,2	в. ч. М из 2,1	р. п. L±Ci L2C2	н. ч. в. ч. К-тип при ЬХС1=L2C2	р. п. н. ч. если Zi=0 при Z2=0	в. ч. при Zi=0, если Ζι~ 0 р. п.
	4	р. п.	р. п.	2 р. п. 1 р. п. при LiCi=L2C2 К-тип	р. п. когда LiCiSs L2C2	2 р п. 1 р. п. если Z |=оо при Z2=со	2 р. п. 1 р. п. если Zi=00 при Z2=00
	5	р. п.	в. ч. р. п.	2 р. п. 1 р. п. если Ζλ=0 при Ζ2=00	р. п. в ч. если Zi=00 при Z2=ОО	2 р. п. 1 р. и. 1) если Zi=со при Z2=оо 2) если Zi=0 при Z2=0	2 р. п. и в ч. р. п. и в ч. если Ζι=οο при Z2—0 если Ζι=0 при Z2=oo
	6	II. ч. р. и.	в ч. р. п.	2 р. п. 1 р. п. если Z i=0 при Zo=0	н. ч. р. п. если Z=00 при Z2=00	н. ч. и 2 р. п. II. ч. и 1 р. п. при Zi=0, если Z2=со при Zx=00, если Z2=0	2 р. п. 1 р. п. при Zi=со, когда Z2=со при Zi=0, когда Z2=0

для Т-ячейки, составленной из схем фигура 16 для Ζ_λ — схема III и для Ζ₂— схема IV. Частоты /₂ и f з — резонансные частоты Z₂ и Ζ_λ соответственно. При некоторой частоте /_х отношение κ= Ζχ/4Ζ₂==XJXi, где Ζχ и Х₂— реактивные сопротивления схемы III и IV фигура 16 — принимают значение — 1; при частоте /₂ κ=0; для всех же частот между /₄ и /₂ 0 > κ > —1; /i и /_а — частоты среза полосы пропускаемо-сти Э. ф. Точно так же при /₃ κ=0 и /₄κ=—1; для частот между /₃ и /₄ 0 > κ > —1. Таким образом /₃ и /₄ также частоты среза для полосы, заключенной между ними. Э. ф., составленный из Т-ячеек этого вида, это резонансный полосный Э. ф., имеющий две полосы прозрачности от /i до /₂ ^{и от} /з До /₄- В табл. 2 сведены все данные о видах и числе полос прозрачности для Э. ф., составленных из первых 6 схем фигура 16. Номера схем для Z₄ показаны в верхней горизонтальной строке, номера схем для Z₂ — в вертикальном первом столбце. Данные Э. ф., составленного из различных схем, показаны в шРетке пересечения для соответственных схем. В клетках указано число пропускаемых полос, условия для получения одной полосы, а также характер пропускаемых полос. Э. ф., пропускающий низкие частоты, обозначен буквами н. ч., пропускающий высокие частоты — в ч., резонансная полоса частот — буквами р. п.

Выше была приведена классификация Э. ф. по виду схем ячеек и по полосе пропускаемых частот. Практически большее значение имеет ди-ференция различных видов Э. ф. по соотношениям между Z₄ и Z₂, используемым в параллельных и последовательных ветвях ячеек. Все виды Э. ф., разобранных выше, являются примером Э. ф. общего типа, в которых в качестве Z₄ и Z₂м. б. использованы любые полные сопротивления без указания их взаимной зависимости. Практически наиболее употребительны следующие виды Э. ф.: 1) К-фильтр, 2) производный М-фильтр и 3) сложные, или комбинированные, Э. ф.

К-ф и л ь т р ы — такие Э. ф., которые состоят из симметричных Т- или П-ячеек, в которых произведение последовательных Z₄ и параллельных Z₂ полных сопротивлений равно постоянной величине К²} не зависящей от частоты, то есть в которых

Z₁Z₂=K². (82 А)

точно так же

Ζτ -

R

(84)

Т. о. для данной величины Z_tl2R, Z и Zj пропорциональны R с другой стороны, т. к.

ZjZ_x=R

(85)

то при конструировании Э. ф. типа К после выбора величины R> каковая устанавливается, исходя из условий для сопротивления нагрузок, приходится иметь дело только с одной переменной Z₄ (или Z₂) для определения зависимости изменения характеристик Э. ф. с частотой. Цифровые расчеты показывают, что (ZJ2R)² всегда отрицательное число, если Z₄ чисто реактивное сопротивление, почему ур-ия (83) и (84) д_ б. переписаны в следующем виде:

: R

(83А)

Zi =

кчж

(84А)

Знак Ζχ не играет никакой роли в этих формулах, определяя только знак Zj в областях затухания, Z в этом случае противоположно по знаку. Следовательно постоянная поглощения и фазовая постоянная для Э. ф. типа К определяется на фигуре 14 и 15 кривыми для φ== ± 180°. Наконец, т. к. Ζχ/4Ζ₂=(XJ2R)²== U + jV и т. к. для этих Э. φ. V — 0, то ур-ия (83) и (84) м. б. представлены в виде

Z_r=R У 1 + U

(85)

¹ ιΓ ί + и

(86)

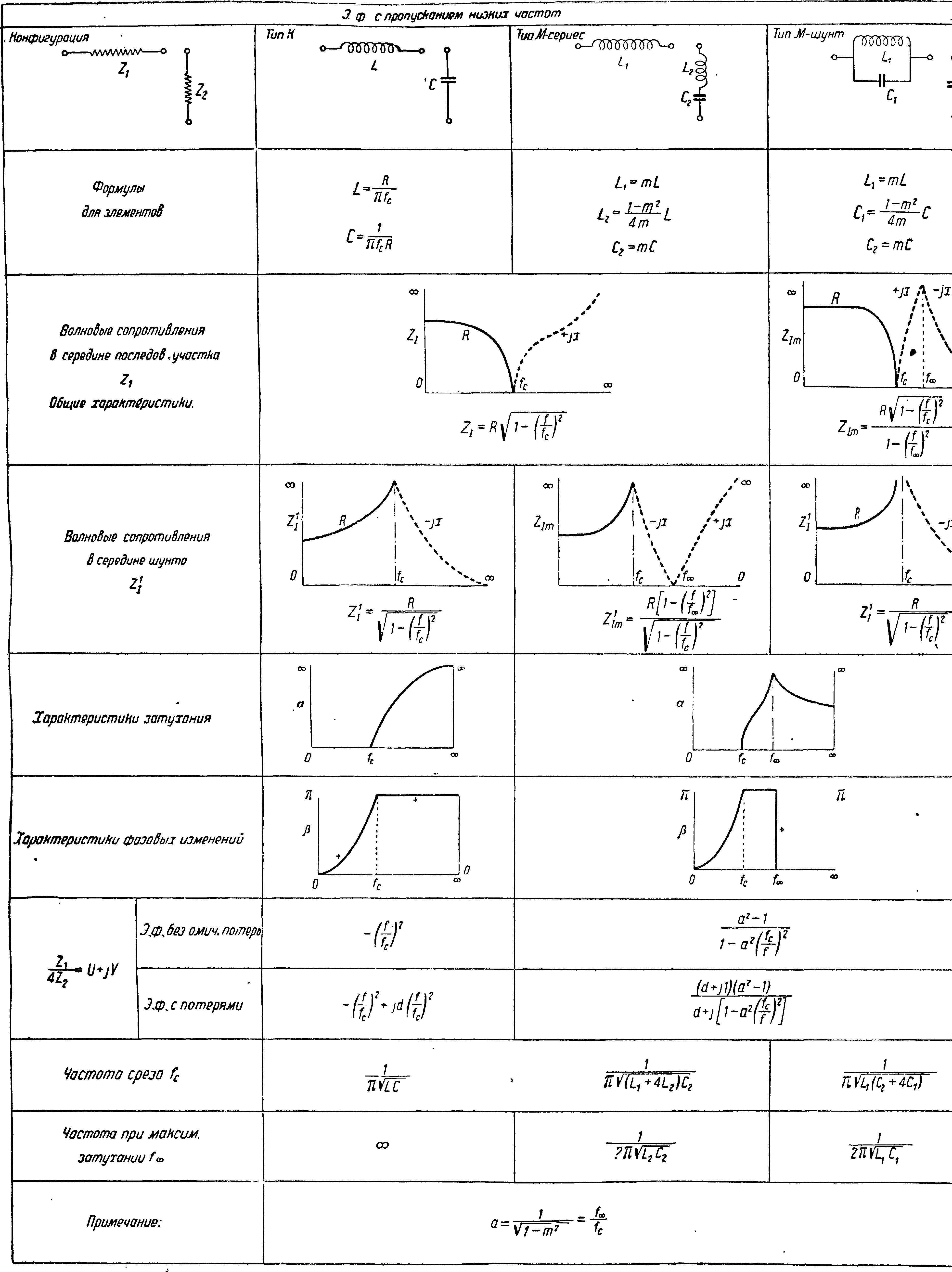
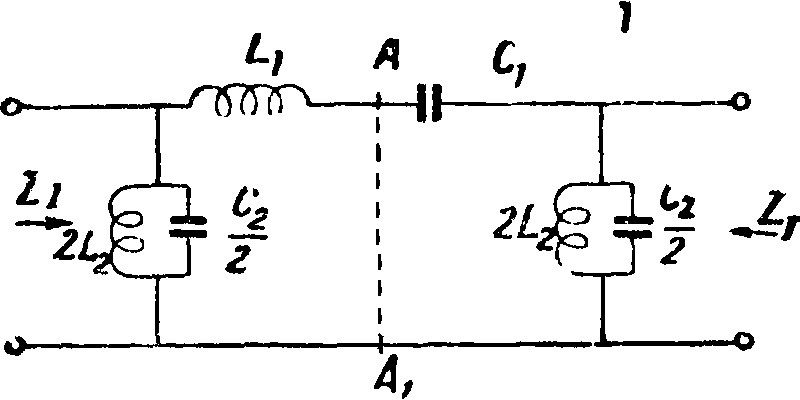
Э. ф. с пропусканием низких частот, тип К. В простейшей форме в этом Э. ф.

Фигура 18.

Это значит, что Ζχ и Ζ₂ должен быть потенциально обратными цепями. Преимущества К-фильтров заключаются в том, что они легко позволяют получить любой ряд полос прозрачности, причем их волновые сопротивления как в Т-, так и в П-ячейках изменяются в каждой полосе прозрачности в тех же пределах величин. Кроме того они приводят к конструированию других Э. ф., дающих лучшие характеристики. В случае резонансных Э. ф. типа К, т. к. Ζχ и Ζ₂ резонируют на той же самой частоте, как это видно из фигура 17, /₂=/з, то есть 2 полосы прозрачности сливаются в одну, распространяющуюся в диапазоне от /₄ до /₄. В этом случае κ=Ζχ/4Ζ₂== 1 при /₄ и при /₄ κ — 0 практически частоты среза не дает. Далее, т. к. Ζχ и Ζ₂ — чисто реактивные сопротивления противоположных знаков, К в формуле (82 А) должен быть чисто омич, сопротивлением. Поэтому для зеркальных полных сопротивлений Zj имеем след, ур-ие:

Ζχ=j/Xz^l+^gj=R 1ЛТЩУ; (83)

в последовательном участке — индуктивность, в параллельном — конденсатор, то есть (фигура 18)

	Zi=j<oL	и Ζ2 =	1. L jcoC ’ C	= R2.
	= Λ ]/” 1 -	coL >2 2R ) ~~	R Y -	a>2 LC
	=	κγ -	ш··		(87)
		^ π V LC			(88)
где /„-	- частота среза, соответствующая
при J-	Zi 4Z2	= -i =	a>2c,LC 4		(89)
	<1
	ζι=ν·§		= R,		(90)

откуда, комбинируя ур-ия (88) и (90), находим

Все прочие Э. ф. с пропусканием низких частот и ф-лы, необходимые для расчета, приведены в общей табл. 3. — Э. ф. типа К с пропусканием высоких частот показан на фигуре 19.

			ml.
!l	h il	Г z—	i/π m <
		ψ^Ψ /m	fZm*» 2Уп
Фигура 19.

Таким же точно образом найдем для частоты среза f_x

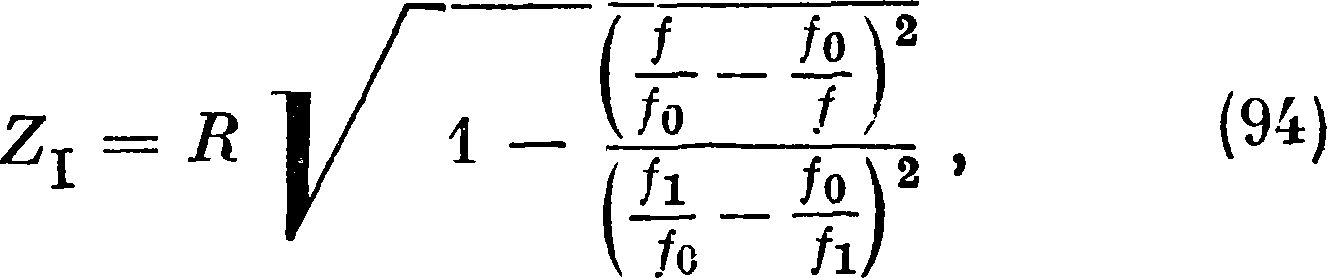
откуда следует, т. к. /₁=^= /₂, что h __ io /о h

или и=УйГж, (95)

1 L

Здесь Z_x=т^_с и Z₂=coZ/, опять —=R² и Ζγ=

^{= R}V 1 ~ (т) * ^ГДе f^{c =} 4nVLCl

Прочие данные см. в таблице 4, общей для Э. ф. с пропусканием высоких и низких частот. Э. ф. типа К с пропусканием полосы частот имеют в последовательном участке резонансную цепь и в параллельном — ангирезонансную цепь. Z_xсостоит из двух реактивных элементов, включенных последовательно, Ζ₂ также из двух элементов, включенных в параллель (фигура 20). В

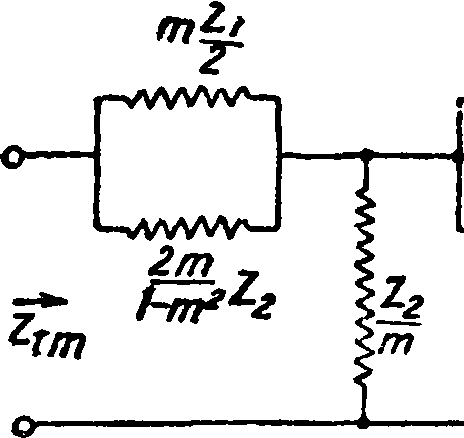
2/77 у

Z/m

-о

mZt

Фигура 20.

подобном Э. ф. все частоты ниже одной из частот среза f_x и выше другой частоты среза /₂ поглощаются, а частоты между этими частотами среза пропускаются. Т. к. Z_x и Z₂ потенциально обратные цепи по отношению к какой-либо величине сопротивления R, то

%=£₁₌Л*или Л=У%=У%. (91)

откуда

VLfi 1=V, Z_x=j («L, - ^) =

= /“oA (92)

1

соответствует частоте резонан-

^{где ω}°⁼

са Ζ^

а>0 ²

ω )

( _ u>pL ^

2Я V 2jR ) Uo

·~τ»>*Α £-?)·

Для устранения L_x и C₂ из этого ур-ия найдем выражения для частот среза f_x и /₂. При /₂

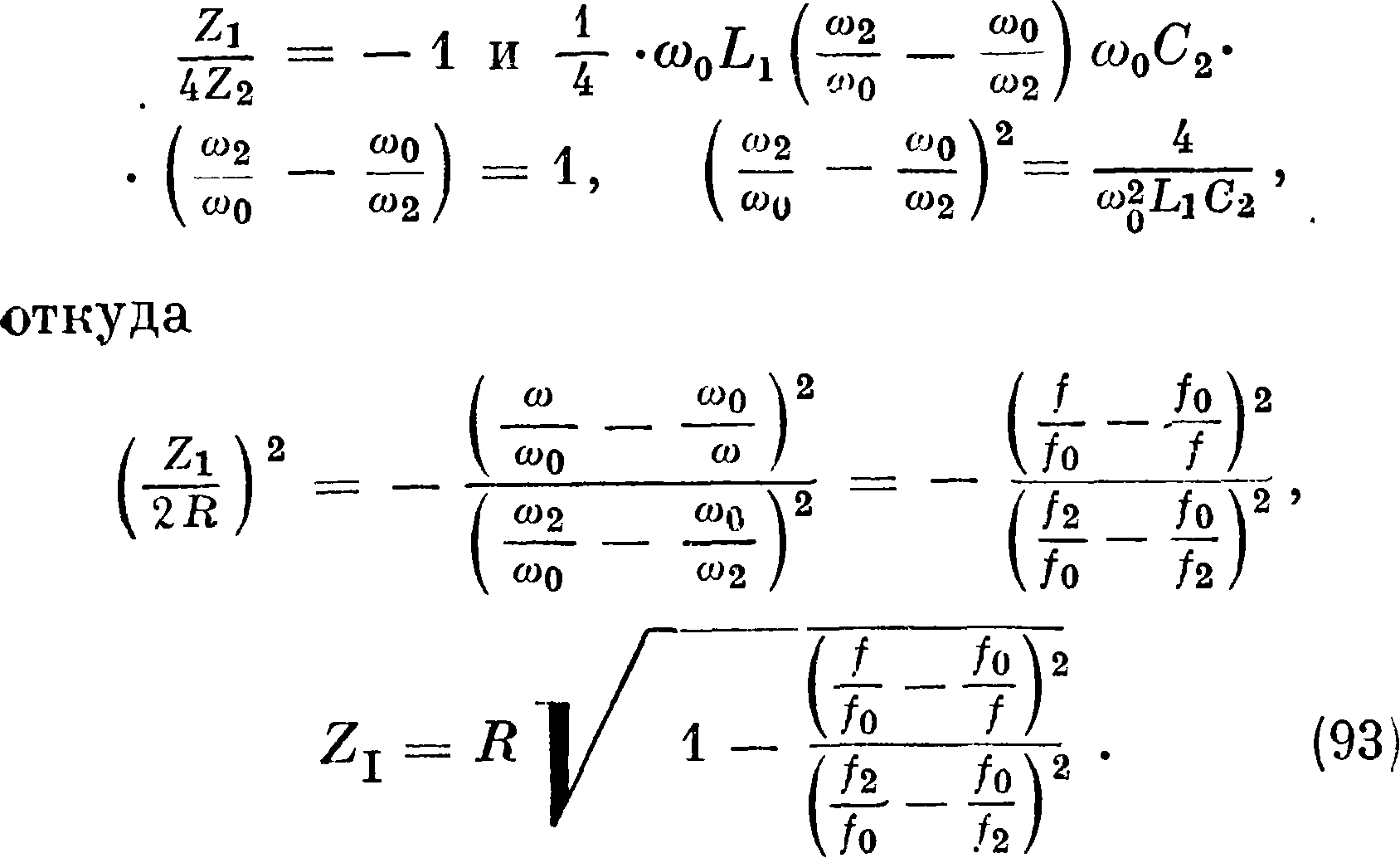
то есть частота резонанса последовательного участка простого резонансного Э. ф. типа К есть среднегеометрическое двух частот среза /_х и /₂. Но т. к. при частоте /₀ Ζ_χ=0 и Ζ₂=οο, то она является в то же время той частотой, при которой полосы прозрачности или соприкасаются друг с другом или «сливаются». При частотах среза, г. е. когда fL=Ч ₌_ι

4Z₂ 4R2 ¹ ’

Z₁=db/2-R. (96)

Т. о. для частоты среза /_А L_x2nf_x — =

= —2 R и для частоты /₂ L₂2nf₂ — -

= + 2R. ^{1 712}

Решая эти ур-ия, находим расчетные формулы для составляющих элементов Э. ф.

I __ R 1 Я (h - h)	(97)
P h — h 1 ~ 4nUhR ’	(98)
r (h-h)R 2 4π/ι/2	(99)
_ 1 2 я(/2-/1)Д·	(100)

Аналогичным образом находятся расчетные ф-лы и для Э. ф., задерживающего полосу частот. Все эти ф-лы сведены в таблице 4.

Э. ф. М по своим характеристикам пропускаемое™ в общем совершеннее, чем Э. ф. К. Фильтры М обычно являются производными от Э. ф. типа К. Преимущества их заключаются в той, что они дают возможность зафиксировать не только частоты среза, но также и некоторые частоты, при которых можно установить максимальное затухание. Благодаря этому возможно получить более резкое наступление среза и более совершенным образом снять некоторые наиболее неприятные для хорошего воспроизведения сигналов частоты, чем это возможно при Э. ф. типа К. Далее возможно при тщательном конструировании Э. ф. получить более практически постоянное волновое сопротивление Э. ф. на значительном участке пропускаемых полос. Э. ф. типа М обыкновенно имеют то же самое волновое сопротивление и полосу прозрачности, как и Э. ф. типа К, производными от которого они являются, но кроме того имеют очень большое или бесконечное затухание на некоторой частоте, близкой к частоте среза. Э. ф. типа К, производным от которого является Э. ф. типа М, называется прототипом. Если прототип К имеет по ур-ию (83) волновое сопротивление

^Z*=V^RY +St)’

то производный от него Э. ф. типа М должен иметь то же самое волновое сопротивление для всех частот, а также=0, когдα= 0.

Индексы относятся здесь к элементам ячейки

Э. ф. типа М. Последнее условие ряется, когда Zlm=mZlt где т — произвольно выбранная. Тогда	удовлетво- постоянная,
ZJcm — ZimZ2m + 4 z2w)	=
= У mZxZ2m (l + Щ),	(101)
откуда, т. к. Zhm — Zft, находим:
у _ I 7 1 1 ~ т2 m ^ V 4т ]*	(102)

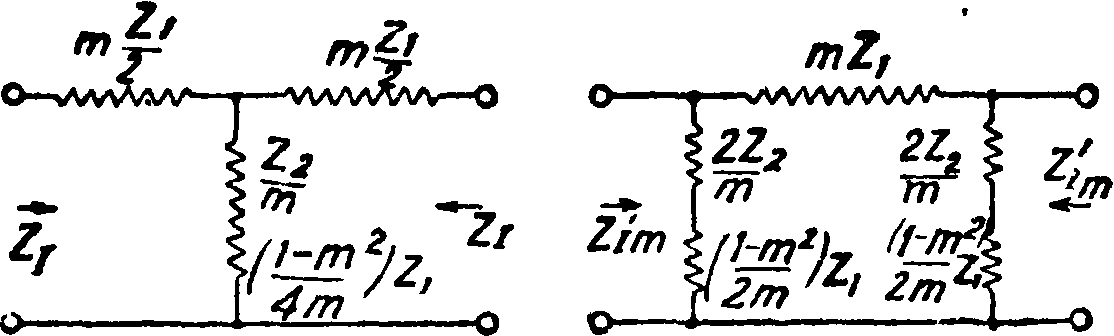
На фигуре 18 показаны Т- и П-ячейки Э. ф. типа М—производные от Э. ф. типа К, показанного на той же фигуре. Волновое сопротивление для П-ячейки определится из ур-ия (60), если в него подставить величины для Z_lm=mZ₁ и Z_2m =

1 ry i 1 — m2 _Ύ.

⁼ m ⁺ 4m

тогда

17 ^w2(t|-)

^zL=^zi[¹ + (¹-^m2)4%] =

= Zi [1 + (1 - nfl) (g)²]. (Ю4)

Фактор [l + (1 — m²) определяет степень изменения волнового сопротивления Э. ф. типа М по сравнению с Ζχ для прототипа, по отношению к к-рому он является производным; он зависит от выбранной величины для т, а также от частотной характеристики Э. ф., определяемого

^. Т-ячейка М-фильтра м. б. спарена с любых концов со своим прототипом, то есть с а. ф. типа К или с одним концом полуячейки Г, имеющей волновое сопротивление Ζχ. С П-ячейкой Т-ячейка м. б. соединена через посредство полуячейки Г так, как показано на фигуре 19. Показанные на фигуре 18 Э. ф. типа М называют Э. ф. типа М, производными для последовательных ветвей. Таким же образом м. б. получены Э. ф. типа М, производные для параллельных ветвей, показанные на фигуре 20. Здесь

Ч

!+(!

-^т%)т

(105)

Из ур-ий (104) и (105) имеем следующее соотно-

^ζι«

шение

Ч

_ζ — и если прототип для рассматри-ваемых М-фильтров — Э. ф. типа К, то Ζ_γ Ζ=ZrZ=Я².

J-m J- J-

Характеристика затухания М-фильтров отличается от Э. ф. типа К гл. обр. характером затухания в зоне непрозрачности. Затухание 3. ф. типа М зависит от т. к. Д,¹=(— от-

рицательное число, к-рое при увеличении частоты попеременно увеличивается по величине от 0 до сю, уменьшается от сю до 0 (в зависимости от схемы Z_t) и может принимать любое возможное отрицательное значение; фактор 1 + (1 — т²) ~ м. б. положительным или отрицательным. Он меняет знак, когда 1 + (1 — m²) ^z*-=0 или

42г 1 -m2 ’

то есть любая величина Z₁/4Z₂ определяется величиной 1/1 — т². При тех частотах, при которых Э. ф. типа К имеют конечное затухание, так как Zj/4Z₂ конечно, Э. ф. типа М имеют бесконечное затухание, т. к. Д,¹—=сю; чем ближе ш 4^2w

к 1, тем выше это затухание. Однако срез в характеристике затухания Э. ф. получается более пологий. Величина т обычно выбирается с таким расчетом, чтобы получить постоянство волнового сопротивления Э. ф. в полосе прозрачности. В этом отношении наилучшие результаты получаются для значений m, близких к 0,6, что видно из фигура 21, где даны кривые зависимости Ζ_χ и Ζ^ от Zj/4Z₈ в полосе прозрачности для Э. ф. с различными величинами т. Фазовые характеристики Э. ф. типа М также несколько отличаются от характеристик для Э. ф. типа К, что наглядно видно на фигуре 22", где приведены эти характеристики в символич. форме для обоих видов Э. ф. В Э. ф. типа М обе частоты с бесконечным затуханием /_1оо и /_2оо расположены симметрично относительно /₀; т. о.

(106)

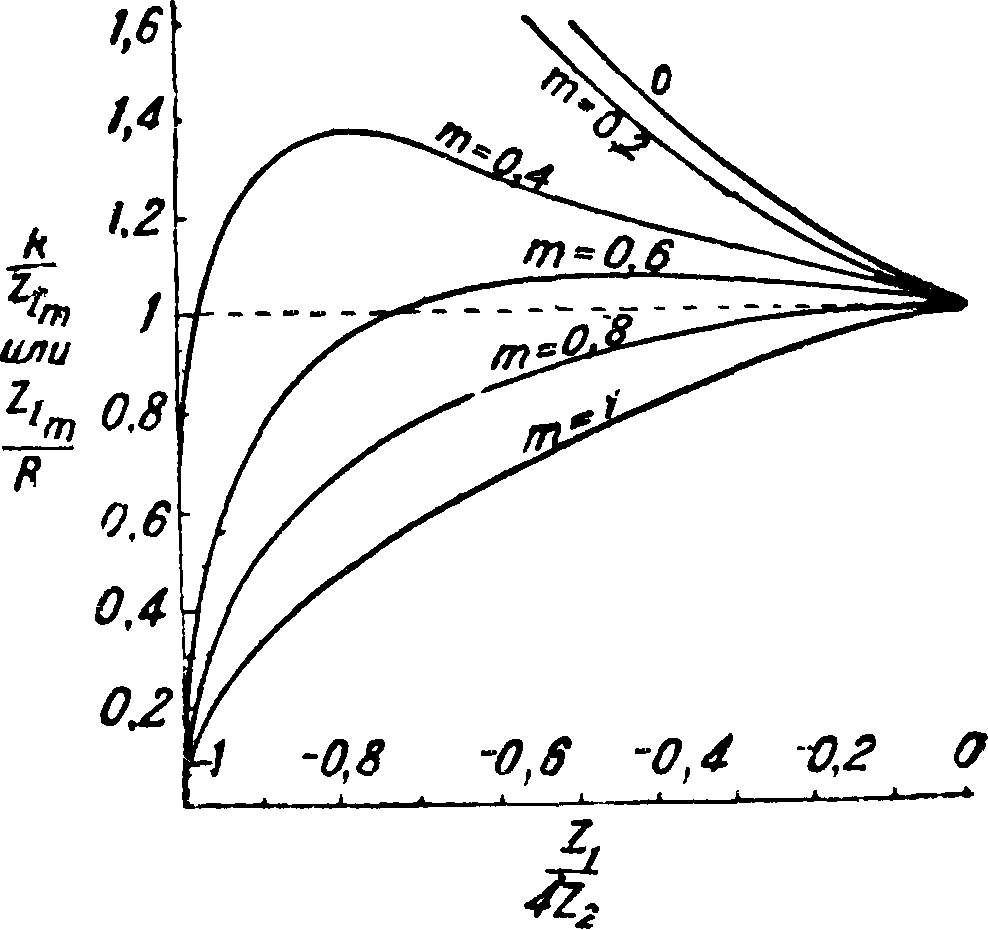
Фигура 21.

to — V floofzoo — У /1/2·

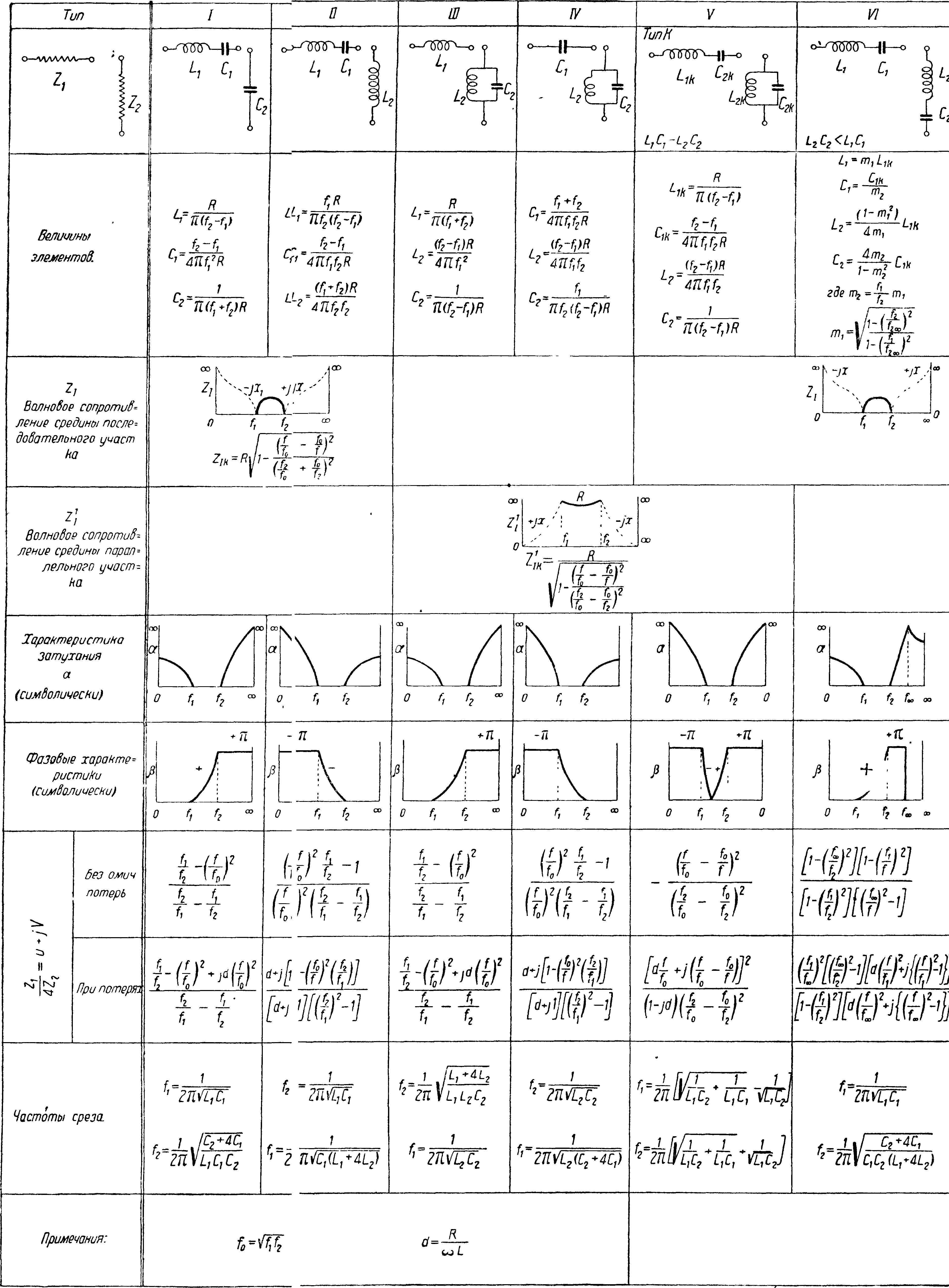
Расчеты в Э. ф. Все расчетные данные сведены в таблице 3 и 4. Таблица 3 относится к Э. ф. с пропусканием только низких и только высоких частот, табл. 4 — к полосным резонансным

Э. ф., а также к ре-жекторным Э. ф., задерживающим полосу частот. В таблицах даны: 1) Характеристики волновых сопротивлений для Т-иП-ячеек (Ζχ, Ζχ, ^Zlm> ^zim) затухания и фазовых изменений для Э. ф. без омических потерь. 2) Ф-лы для значений элементов Э. ф. (Z_1? Z₂), для волновых сопротивлений, отношения Z_xjkZ₂ в Э. ф. без омич, потерь и в Э. ф. с потерями, для частот среза и частот, соответствующих максимальному затуханию. Форма кривых дана в символич. виде. Для составления Г-полуячейки необходимо в последовательный участок включить сопротивление z₁ и в параллельный участок 2Z₂, для составления Т-ячейки—в 2 последовательные плеча сопротивления — Ζ_χνι в параллельный участок Z₂,

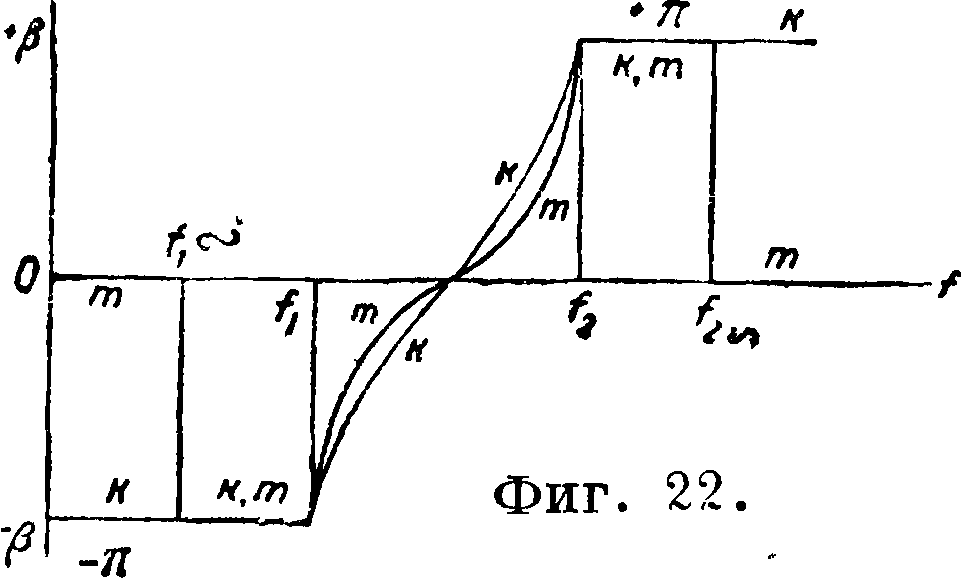
П-ячейки — в параллельные участки 2Z₂ и в последовательные Zj. Выражения для отношения сопротивлений соответствуют постоянной затухания и фазовой постоянной для полной Т- или П-ячейки. Постоянная затухания, а также фазовая постоянная для половины секции равна точно половинам величин этих параметров для полных ячеек.

Э. ф. с трансформаторами. Трансформаторные Э. ф. отличаются от обычных Э. ф. тем, что в них имеет место на всех частотах транс-

Τ. θ. Цоп. т.

Т, Э. Доп. т формирование относительно отдельных участков Э. ф. величин полных сопротивлений с повышением или понижением их действующих величин. Ячейка трансформаторного Э. ф. действует так же, как комбинация обычной ячейки и идеального трансформатора. Для уяснения действия трансформаторного Э. ф. лучше всего установить эквивалентность схемы этих Э. ф. схеме обычных Э. ф. В качестве примера рассмотрим схему фигура 23, а, представляющей идеальный трансформатор, одна из обмоток которого зашун-тирована ZJ. Если коэф. трансформации этого трансформатора слева направо η, то трансформация полных сопротивлений происходит в отношении η². Пусть схема ячейки 23, b эквивалентна схеме 23, а. При разомкнутых концах 3—4 имеем на концах 1—2 обеих схем Z_s=Z_A + Z_c. При разомкнутых концах 1—2 имеем на концах

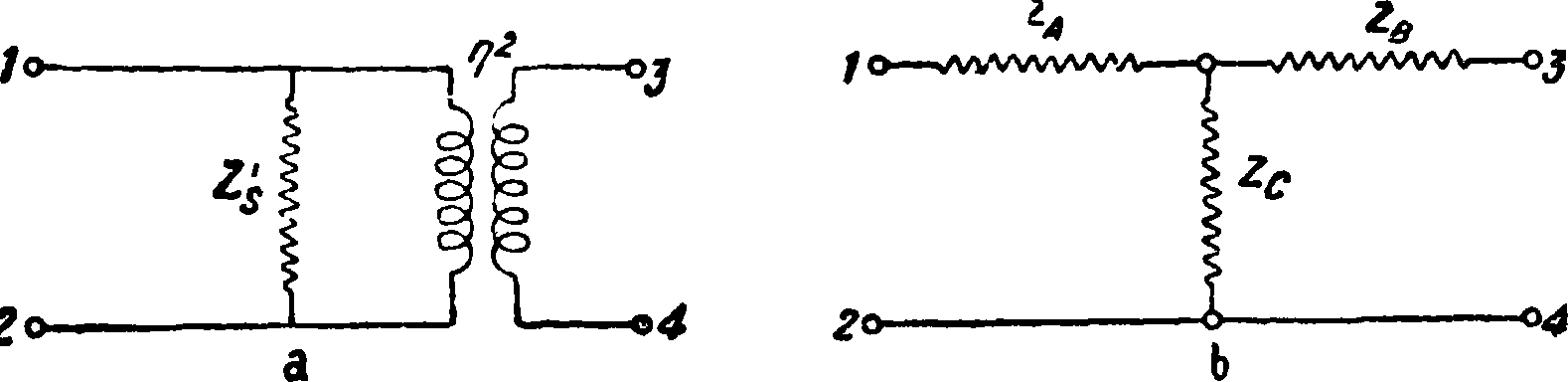
/о——wvwVCww»--1

20-

10-

20-

Фит. 23.

3—4 η² Z_s=Z_B + Z_c. Для измерений при замкнутых концах имеем соответственно

О=Z_A

ZbZc Zb + ^zc

О=Zj9 +

ZaZc Za + Zc *

Из этих ур-ий находим следующие выражения для элементов эквивалентной ячейки:

Ζ_Λ=(1 — η) z’s Z_B=П (! — П) Zs=— ηΖ_Α

Z(j=η Zg

(107)

Аналогичным образом для схемы фигура 23, с найдем эквивалентные элементы эквивалентной П-ячейки фигура 23, d:

Ζ=-^—,Ζ· Ζ;=ηΖ_Β

А η — { s’ В ^s

z_n =

(108)

1 -n‘

- nZ_A.

Для схемы фигура 23, а нельзя подобрать эквивалентность П-ячейки, а для схемы фигура 23, Ь — эквивалентность Т-ячейки. На фигуре 24 показаны примеры применения принципа эквивалентности для изучения трансформаторных Э. ф. с последовательным превращением первоначальной схемы с трансформацией в эквивалентную без трансформации. Основные преимущества Э. ф. с трансформаторами следующие: 1) они позволяют устранить емкостное влияние между входными и выходными зажимами Э. ф., 2) ограничиться меньшим количеством элементов, чем это необходимо в простой схеме.

Сложные, или составные, Э. ф. представляют собой последовательное соединение нескольких простых ячеек различного вида, причем соединение это производится по всем правилам, отмеченным выше. Характеристики таких Э. ф. получаются построением путем наложения друг на друга характеристик составляющих звеньев. Сложные Э. ф. в насто ящее время нашли очень широкое распространение. Их основное преимущество заключается в том, что путем использования в таком Э. ф.

с

i!

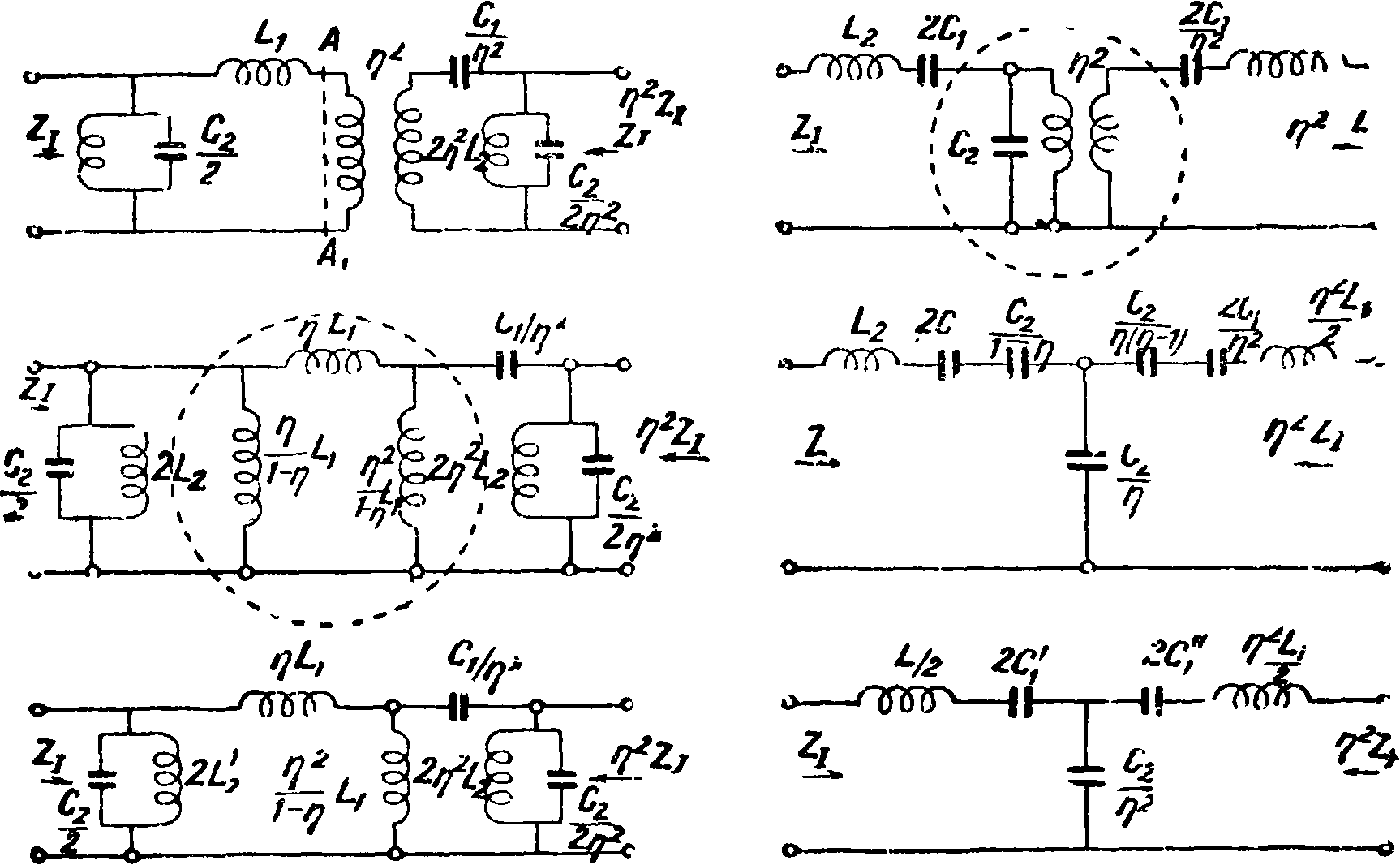
Фигура 24.

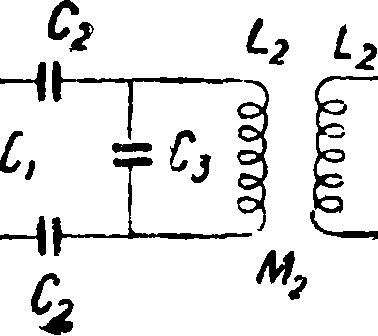
ячеек Э. ф. с различными характеристиками оказывается возможным построить Э. ф., обладающий теми же электрическими данными, что и Э. ф. с одинаковыми ячейками, при значительном уменьшении его стоимости за счет меньшей затраты материалов в элементах Э. ф. при меньших электрич. величинах последних. Примером сложного Э. ф. может служить полосный г

С

М. ^

о-ТЯЯЛГ—^ -

h

t-i

м_г

-ИППЛГ^-о

ш

ινΤΗϊΛ-

II

чь

Фигура 25.

Э. ф., примененный в аппарате многократной телефонии на высоких частотах фирмы «Теле-функен», показанный на фигуре 25,а. На той же фигура 25,6 показана эквивалентная схема этого Э. ф., состоящая 1) из 2 ячеек конденсаторных Э. ф. с пропусканием высоких частот, 2) одной ячейки резонансного типа и 3) двух Г-полуячеек по концам с пропусканием низких частот. В действительной схеме последние включены по сбалансированной схеме. Данные этих схем нетрудно рассчитать, пользуясь табл. 3 и 4.

Параллельная работа Э. ф. В случае работы нескольких Э. ф. на одну общую

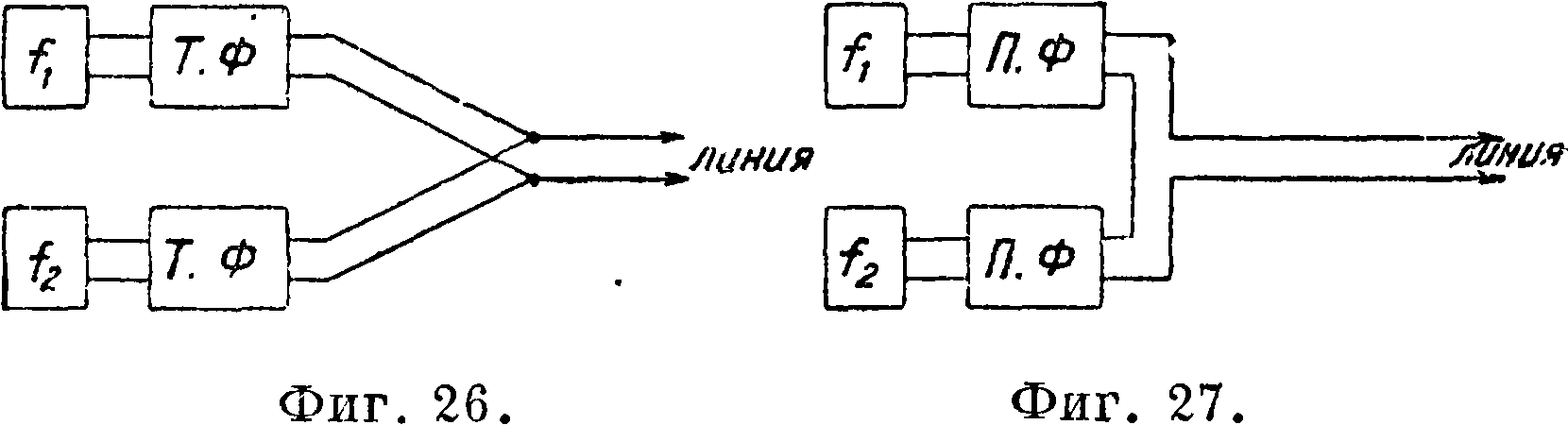
цепь возможны следующие включения Э. ф. для осуществления их работы в этих условиях. Э. ф., составленные из Т-образных ячеек, вклю чают относительно входа линии параллельно по схеме фигура 26, фильтры с П-ячейками после до-, вательно относительно линии по схеме фигура 27. Непосредственное параллельное включение последних по схеме фигура 26 неосуществимо по той причине, что волновое сопротивление П-об-разных ячеек в полосе затухания стремится к короткому замыканию.

Компенсаторы волнового сопротивления Э. ф. Волновое сопротивле-

2,099//Н

ние всех Э. ф. в полосе прозрачности изменяется в зависимости от частоты. Эта зависимость всякого сопротивления от частоты в полосе пропускаемое™ приводит к нарушению равенства сопротивления Э. ф. с сопротивлением нагрузки, а следовательно к появлению отражения. В настоящее время для получения равномерной частотной характеристики Э. ф. в полосе пропускаемое™ применяют так. наз. компенсаторы волнового сопротивления, позволяющие значительно снизить эффект непостоянства сопротивления Э. ф. от частоты. Предложен целый ряд таких компенсаторов, по электрич. схеме напоминающих схемы Э. ф. и представляющих собой ряд индуктивных и емкостных сопротивлений, включенных частью последовательно частью параллельно компенсируемому Э. ф. В последнее время появилась тенденция выравнивать волновое сопротивление Э. ф. в полосе пропускаемое™ без компенсатора путем комбинирования схемы самого Э. ф.

Конструирование Э. ф. сводится 1) к расчету элементов электрических фильтров конденсаторов и катушек и 2) к такому расположению отдельных элементов в схеме, чтобы они действовали, не влияя друг на друга. Катушки Э. ф. располагаются т. о., чтобы плоскости витков трех лежащих по соседству не связываемых катушек были взаимно перпендикулярны друг к другу. Весь Э. ф. как правило экранируется со всех сторон железным кожухом, к-рый не должен иметь щелей. Соединительные провода Э. ф. с другими частями схемы пропускаются в железных или освинцованных трубках, заключающих в себе и входные зажимы. Если в Э. ф. отдельные элементы связываются между собой индуктивно, то катушки связи разделяются параллельно расположенными заземленными электростатическими экранами. Конденсаторы Э. ф. располагаются между катушками т. о., чтобы их соединение с остальной схемой требовало минимума соединительных проводов. Для обеспечения точной работы Э. ф., в особенности полосных, требуется поддержание большой точности в величинах элементов; для конденсаторов практически достигаемая точность оценивается 0,3% и для катушек до 1—2%. Однако, т. к. во многих случаях требуется большая точность, в Э. ф. находят применение катушки специальной конструкции — заэкранированные — с возможностью установить индуктив ность с требуемой точностью с помощью короткозамкнутой катушки, расположенной вокруг экранирующего чехла катушки и вращаемой относительно оси расположения основной катушки в экране. Для исследования и измерения собранных Э. ф. существует специально разработанная методика измерений. Б последнее время в качестве элементов полных сопротивлений в Э. ф. применяются пьезоэлектрич. кристаллы.

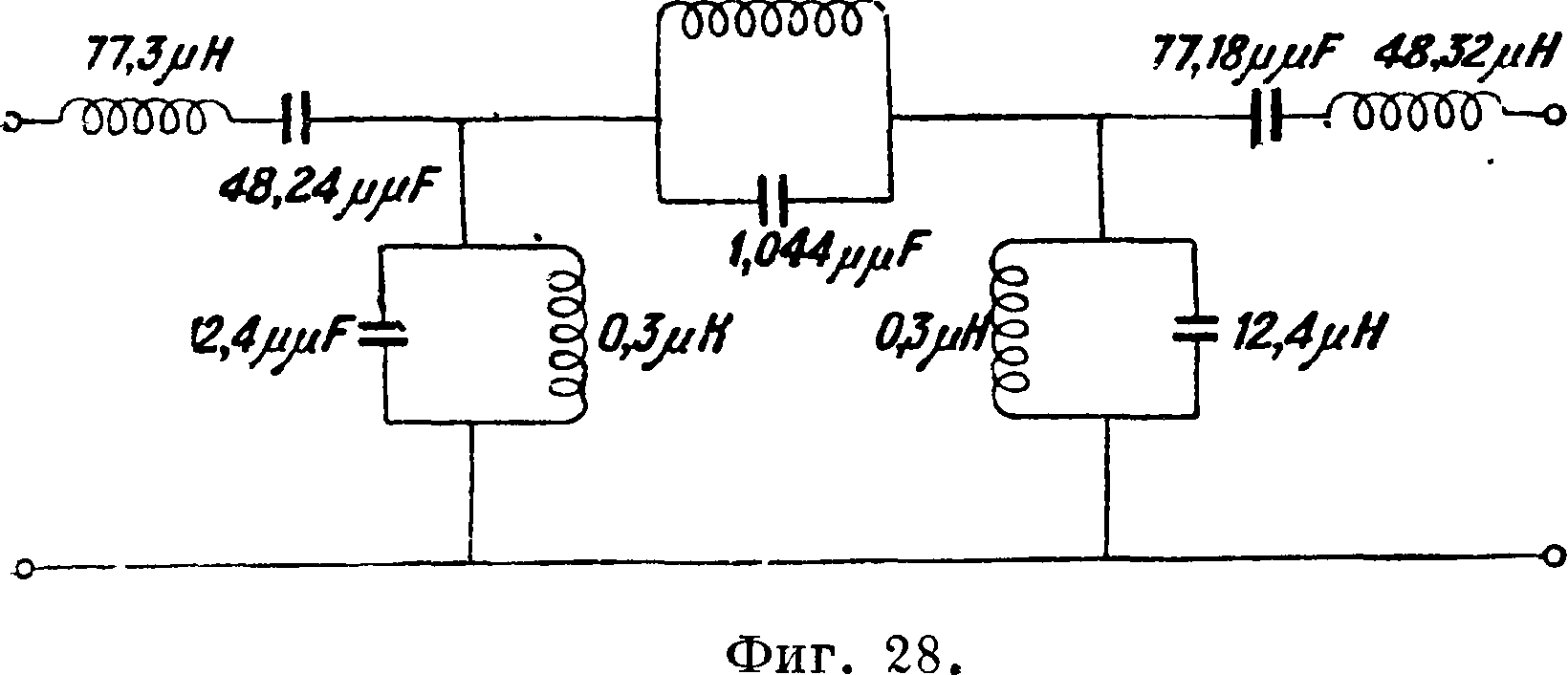
Ячеечные Э. ф. для высоких (радио) частот. По мере увеличения частоты, при которой Э. ф. должен работать, величины катушек и конденсаторов, рассчитанные обычным способом по табл. 3 и 4, становятся все меньше и меньше, при частотах порядка 1 · 10⁶ Hz величины некоторых катушек становятся уже настолько малыми, что практически они уже невыполнимы. На фигуре 28 показана схема Э. ф., рассчитанная для работы при частоте

2,6 · 10⁶ Hz; на схеме показаны требуемые на основании математич. расчета величины элементов этого Э. ф. Одна из требуемых индуктивностей в этом Э. ф. 0,3 р.Н соответствует индуктивности, получаемой в прямом проводе длиной несколько см, индуктивность 2 μΗ при диам. катушки 2—3 сантиметров обеспечивается двумя витками. Т. о. индуктивность таких катушек уже соизмерима с индуктивностью соединительных проводов в Э. ф. Фильтры с такими величинами индуктивностей конечно практически осуществить нельзя. Для того чтобы конструирование Э. ф. для таких высоких частот практически бы-

•—]	*1	1 £ с^-ГП-= 1 UU J	^ ; I——и—:	[ · t.-V 0000 j—о
о—у QQ00 j- 1	I I 1Л	й & 1 Г!	I Л. т
	L..i Г..1	1	*----------J	11-----V vUUy J—O
о—у 0 00 Q J-|Н	У η-? 1 L·.--------1		JLh 1-----------1	HI—iQQQO /—о

Фигура 29.

л о осуществимо, в этих Э. ф. используют схемы Э. ф. с трансформаторами, с помощью которых индуктивность требуемых катушек приводят до практически реализуемых величин. Конденсаторы же, особенно в параллельных ветвях, становятся здесь также чрезвычайно малыми, и они осуществляются путем образования емкости между отдельными цепями Э. ф. и экранами, которые в этих Э. ф. устраиваются двойными. При очень высоких частотах каждый трансформатор с конденсатором в последовательном соединении заменяется эквивалентной схемой П-ячейки, составленной из конденсаторов. Так как один из этих конденсаторов в эквивалентной конденсаторной схеме идеального трансформатора имеет отрицательное емкостное сопротивление, практически не реализуемое, то в этих Э. ф. применяют схемы, в которых отрицательное емкостное сопротивление поглощается положительным емкостным сопротивлением конденсатора, включенного в параллель и имеющего большую емкость. На фигуре 29 изображена схема такого Э. ф., яв-

ляющегося эквивалентом схемы, показанной на фигуре 28. На фигуре 29 для наглядности показаны все промежуточные процессы составления такого Э. ф. В радиотехнике Э. ф. часто также назы вают систему из двух индуктивно- или емкостносвязанных резонансных контуров, широкая полоса пропускаемости у которых достигается за счет образования двухволнистости настройки при достаточно сильной связи контуров.

Лит.: Ш. и Т., Четырехполюсники и электрич. фильтры, М., 1934; Листов В., Электрические фильтры, М.—Л., 1927; его же, Курс многочастотной проводной связи, 1932; II wain К. М,с a. Brainerd J., High-Frequency Alternating Currents, N. Y., 1931;

S h e a T., Transmission Networks a. Wave Filters, N. Y., 1929; Вагнер К., Цепные линии и волновые фильтры, «Радиосборник секции радиоспециалистов ЦС ОДР», ч. 2 и 3, М., 1930; Eichelberger С., Kettenleiter и. Sperrkreise, «Bibliothek des Radio Amateurs», В. 23, 1923; Z о b e 1 О., Theory a. Design of Uniform a. Composite Wave Filters, «Bell System Technical Journal», 1923, v. 2, 1; Zobel O., Transmission Characteristics of Electric Wave Filters, ibid., 1924, v. 3, 4; Darnell P., Kahl W., Precision Filters, «Bell Laboratories Record», 1934, v. 12, 12; Johnson K. a. Shea T., Mutual Inductance in Wave Filters with an Introduction on Filter Design, «Bell System Technical Journal», 1925, v. 4, 1; Campbell C., Physical Theory of the Electric Wave Filters, ibid., 1922, v. 1, 2; Campbell C., Cisoidal Oscillations, «Trans. AIEE», 1911, v. 30, April; Reed M., Electrical Wave Filters, «Experimental Wireless», 1930, v. 7, 78, 79, 80, 81, 82, 83, 84; Kamaj a-c h i Z., К a t о К., Chiba К., N a g a i T., The Sending End Impedance of Four Terminal Transmitting Networks, «Journal of Inst. Teleg. a^ Teleph. Engineers of Japan», 1933, 12, October, p. 992; Beer C., Little G-., The Design of Filters for Audio Frequencies, «Post. Office Elec. Journ.», 1925, v. 17, Jan.; CohenL., Electric Filter Circuits, «Journ. Franklin Inst.», 1925, v. 195, May; David P., Les Filtres 61ectriques, P., 1926; D e 1 1 e n b a и g h F., .Electric Filters, «QST», 1923, July, August; Kupfmiiller K., Ueber Einschwing-vorgange in Wellentiltern, «Elektrische Nachrichten-Tech-nik», 1924, November; Lange, TMorie des Filtres Electriques, «Ann. des Postes, T616gr. et T616phonie», 1923, Octobre; Peters L., Theory of Electric Wave Filters Built of Coupled Circuit Elements, «Trans. AIEE», 1923, v. 42, May; Wagner K., Kettenleiter u. Wel-lenseile, «Elektr. Nachrichten-Technik», 1925, B. 5, H. 1, Jan.; Wheeler H., Murnaghan F., Theory of Electric Wave Filters Containing a Finite Number of Sections, «Phil. Mag.», 1923, v. 6, 34, July; Z о b e 1 O., Distortion Correction in Electrical Circuits with Constant Resistance Recurrent Networks, «Bell System Techn Journal», 1928, v. 7, 3, July; B a r t 1 e t t A., The Theory of Electrical Lines a. Filters, L., 1930; K e η n e 1 у A., Electric Lines a. Nets, N. Y., 1928; Backaus H., Theory of Short Filter Circuits, «Jahrb. d. drahtl. Telegr. u. Telephonie», 1925, B. 25, Η. 1—6; Winter-Gun-ther H., The Theory of Filter Circuits, ibid., 1928, B. 32, H. 1; Johnson K., Shea T., Wave Filters, «Bell System Technic. Journ.», 1925. П. Куксенко.