> Техника, страница 94 > Электрический ток

Электрический ток

Электрический ток, упорядоченное движение электр 14. зарядов. Внешне Э. т. проявляется в том, что тело, по к-рому он проходит: 1) всегда окружено магнитным полем и 2) выделяет тепло; последнее не имеет места только в том случае, когда проводящее тело находится в состоянии сверхпроводимости (смотрите).Первоначально Э. т. объяснялся движением особой «электрической жидкости». Впервые Максвелл на основе экспериментальных исследований Фарадея дал математическую теорию электромагнитных явлений вообще и теорию Э. т. в частности. В теории Максвелла устанавливается связь в форме диференциальных уравнений между распределением и движением (током) электрич. зарядов и динамикой возбужденного

Таблица 3.—Значение <5 для некоторых диэлектриков.

Диэлектрики	Диэле ктрич. посто янная €	Сопротивление ρ, Q-см	Угол потерь <5		Напряжение пробоя (kV) между плоскими пластинами на расстоянии
Диэлектрики	Диэле ктрич. посто янная €	Сопротивление ρ, Q-см	800 ΗΖ 104	600 kHz 101	0,2 миллиметров	1 миллиметров	10 миллиметров
Слюда.	5-4-8	2.1015.^2.1017	2-4-10	i,⁷	19	60	500
Стекло.	5-4-9	5-1013	13С4-240	44-130	6	124-20	90-М 000
Бумага(парафин).	—	—	804-100	480	—	30	1804-200
Пертинакс.	4,8	1-109	250	£304-390	—	—	1С04-200
Парафин.	1,9-2,2	1.1016-^.3.1018	0,8	3-4-9	—	30	904-500
Воздух.	1		0	0	1,2	8,2	23

этими зарядами электромагнитного поля (смотрите М акевелла уравнения). Теория Максвелла устанавливает общие формальные соотношения между основными электромагнитными величинами, не входя в рассмотрение физич. природы этих величин. При этом основной закон Э. т.— закон Ома

J=σΕ, (1)

где Έ—напряженность электрич. поля, j— плотность Э. т., а а—уд. проводимость, являющаяся для теории Максвелла опытным фактом. Задачей же физич. теории являются истолкование ур-ия (1) и объяснение наблюдаемых закономерностей для величины ст, гл. обр. в отношении ее зависимости от t°.

Согласно современным взглядам, представляющим дальнейшее развитие воззрений Лоренца, Э. т. есть фактич. движение электрич. зарядов, причем движение упорядоченное, то есть такое, что в каждом месте большинство электрич. зарядов движется преимущественно в определенном направлении, а в двух достаточно близких точках эти направления не м. б. обратными. Электрич. заряды распадаются на два резко разграниченных класса: 1) электроны (смотрите) и 2) ионы (смотрите).

Соответственно данному выше определению Э. т. обычно разделяли вещества на два класса: 1) вещества, по которым могут двигаться электрич. заряды,—п роводники и 2) вещества, по которым электрич. заряды двигаться не могут,—непроводники, или диэлектрики (смотрите). Проводники разделяются на две группы: металлические проводники (твердые и жидкие), в которых имеет место движение электронов, и электролиты (смотрите), У которых имеет место движение ионов, и следовательно Э. т. связан с переносом вещества. Абсолютных непроводников не существует совсем (смотрите Пробой), однако одни вещества приближаются по своим электрич. свойствам к идеальным непроводникам, другие, наоборот, показывают значительную электропроводность как электронного, так и ионного характера. Однако эта электропроводность имеет гораздо более низкий порядок величины, нежели электропроводность веществ из класса проводников, и обнаруживает также иную Г-ную зависимость. Эти вещества получили название полупроводников.

1. Металлы. По закону Ома при постоянной приложенной разности потенциалов по проводнику протекает Э. т. постоянной плотности. Так как Э. т. есть движение электронов, можно написать для плотности электрич. тока выражение:

j=neu, (2)

предполагая, что все электроны двигаются с одинаковой средней скоростью и и что в единице объёма имеется п электронов. Сравнивая это выражение с (1), мы имеем:

Т. к. еК есть сила, действующая на электрон, мы видим, что скорость электрона пропорциональна действующей на него силе. Из механики известно, что это характерно для движения с трением. Следовательно закон Ома в сущности утверждает, что в мет электроны двигаются с трением. Согласно же представлениям кинетич. теории газов внутреннее трение обусловливается столкновениями между частицами, благодаря которым движение утрачивает упорядоченный характер и превращается в хаотич. тепловое движение. Т. о. под влиянием внешней постоянной силы (например электрич. поля, если частицы несут заряды, или при наличии градиента t°) частицы газа двигаются с ускорением, а благодаря столкновениям накапливаемое в промежутке между двумя последовательными столкновениями количество движения рассеивается. В результате этих двух противоположно направленных процессов устанавливается стационарный поток, в к-ром средняя скорость частиц пропорциональна действующим на них силам. Рикке, Друде и Лоренц применили эти представления кинетической теории газов к электронной теории металлов. В современных терминах их представления соответствуют следующей физич. модели металла. От атомов отщепляется один или несколько электронов, а ионы размещаются в узлах кри-сталлич. решетки металла. Отщепленные же электроны остаются свободными и могут перемещаться в междуионном пространстве. Ионы не сидят неподвижно в узлах решетки, а совершают небольшие колебания около положения равновесия, в чем и заключается тепловое движение в твердых телах. Когда проходит электрич. ток, электроны сталкиваются с ионами и передают им накопленную в промежутке между двумя последовательными столкновениями энергию, которая затем и выделяется в форме джоулева тепла. Столкновения электронов с ионами и есть согласно изложенным взглядам причина электрического сопротивления. При этом электроны рассматриваются как газ, состоящий из невзаимодействующих между собой частиц. Однако математическая обработка этих физических представлений приводила к выводам, содержащим внутренние противоречия. Эти противоречия вызывались тем обстоятельством, что движение электронов изучалось с помощью методов обыкновенной механики, между тем частицы столь небольшой массы, как электроны, подчиняются законам квантовой механики (смотрите Механика квантовая). Т. о. в современной электронной теории металлов полностью сохранилась прежняя физич. модель, но благодаря применению новых принципов при изучении движения электронов эта модель получила несколько иную интерпретацию, и при этом были получены лишенные внутренних противоречий результаты.

Чтобы получить физич. картину движения электронов в металле, исходя из наглядных представлений, вспомним, что с точки зрения квантовой механики движение электронов гораздо более напоминает распространение tv

световых волн, нежели _

движение материальных частиц. В частности отсюда вытекает возможность перехода электрона через барьер потенциальной энергии также и в том случае, когда высота этого барьера больше энергии электрона. Предположим, что электрон движется с энергией W в пространстве, свободном от всяких сил (фигура 1), и в нек-ром месте встречает барьер потенциальной энергии, высота которого U > W. Тогда имеется определенная вероятность того, что электрон не отразится от барьера, как это следовало бы по классич. механике, а будет продолжать двигаться за барьером. Слово «вероятность» здесь можно интерпретировать т. о., что если бы двигался не один электрон, а много, то часть из них отразилась бы

Фигура i_

обратно, а другая часть прошла бы через барьер. Этот эффект, если представлять себе движение электрона как распространение волны, является аналогом диффракции световых волн, которые могут огибать встречающиеся на своем пути препятствия и продолжать свой путь за ними. Этот результат остается справедливым также и в том случае, когда электрон встречает не один, а целую последовательность потенциальных барьеров.

Предположим теперь, что ионы не совершают теплового движения, а сидят неподвижно в узлах кристаллической решетки. Тогда внутри металла имеется периодич. потенциальное поле, к-рое в каком-нибудь направлении может иметь форму, примерно изображенную на фигуре 2. Тогда электр ш согласно вышесказанному может беспрепятственно распространяться по металлу без всякого сопротивления. Движение электрона в этом случае будет вполне аналогично распространению световых волн в среде с периодическим показателем преломления. Такая среда, остающаяся для света прозрачной, может быть получена, если наложить друг на друга ряд плоско-параллельных пластинок с различными показателями преломления. Конечно отсюда отнюдь не вытекает, что движение электрона в периодич. поле совершенно аналогично движению в свободном пространстве, точно так же как и распространение света в столбике, составленном попеременно из двух сортов пластинок, не вполне аналогично распространению в совершенно однородной среде, и нужно отметить, что при определенных условиях движение электрона в металле, а также и распространение света в нашем столбике становятся невозможными. Однако для нас существенным является тот результат, что, вообще говоря, периодич. поле само по себе не есть причина электрич. сопротивления, что в металлической решетке электрон может без всяких внешних воздействий двигаться прямолинейно и равномерно. Это значит, что при наложении электрич. поля он двигался бы с ускорением, а это и значит, что электрич. сопротивление равно нулю. Кроме этого из изложенных представлений сейчас же вытекает еще один чрезвычайно важный результат. До сих пор, говоря об электроне, движущемся в металлич. решетке, мы подразумевали «свободный» электрон — электрон, отщепившийся от атома. Однако дело по существу не меняется, если электрон прочно связан с атомом, т. к. в этом случае изменится только форма периодич. потенциального поля—барьеры между отдельными ионами станут выше и шире, но у электрона попрежнему останется возможность переходить от одного атома к другому. Прочная связь скажется только в том, что электрон связанный двигается с меньшей скоростью, чем свободный, обладающий той же энергией. Этот результат имеет глубокий физич. смысл, т. к. он показывает, что вещества, электроны которых прочно связаны, отнюдь не являются еще диэлектриками, как это думали прежде.

Изложенные представления позволят нам без труда найти причину электрич. сопротивления. Предположим, что мы имеем очень мелкий порошок из стеклянных осколков. Тогда, несмотря на то что каждый осколок является прозрачным, общая масса будет непрозрачной

для света. Объясняется это неправильным отражением света. Совершенно аналогично обстоит дело и в случае движения электронов, если периодическое поле внутри металла претерпевает в различных местах хаотич. возмущения,— металл становится для электрона непрозрачным. При наложении электрич. поля оно будет сообщать электрону скорость в своем направлении, кроме того электроны будут рассеиваться в местах искажений. В результате получится поток электронов, пропорциональный приложенному полю, что и является характерным для электрич. сопротивления. Происхождение искажений в металлич. решетке обусловливается тепловым движением ионов, вследствие которого они совершают хаотич. колебания около положений равновесия. Эти неправильные колебания и являются источником нарушения правильной периодичности кристаллов. Отсюда вытекает, что электрическое сопротивление должно зависеть от t°. Правда, в этой теории Р-ная зависимость обусловлена тепловым движением ионов, в старой же теории она объяснялась тем, что средняя скорость теплового движения электронов зависела от t°. Это обстоятельство приводило к противоречиям и оказалось неверным. Благодаря способности ионов колебаться около положений равновесия электроны могут обмениваться с ионами энергией, превращая т. о. частично свою механич. энергию в тепловую энергию металлической решетки, которая затем и выделяется в форме джоуле-ва тепла. Точка зрения современной теории на происхождение температурной зависимости электрического сопротивления находит между прочим свое подтверждение в характере этой зависимости для электропроводности при низких t°. Точная математич. обработка изложенных здесь представлений приводит к следующим результатам (в полном согласии с экспериментальными фактами): в области высоких t*

Const ^σ ~ т в области низких t°

(3)

Const ^σ ~ Т5^-

(4)

(Т—абсолютная температура).

Для получения последнего результата является существенным предположение, .что искажения решетки обусловлены тепловыми колебаниями ионов, коюрые при низких t° имеют несколько отличный характер, чем при высоких. При этом существенно отметить, что понятия «низкая» и «высокая» t° имеют здесь совершенно определенный смысл. Для всякого тела имеется характеристич. (т. н. дебаевская) £°, определяемая его упругими свойствами, по обе стороны которой тело ведет себя различно в отношении своих тепловых свойств. Обычно—это t° порядка нескольких сот абсолютных градусов. Другие источники искажения решетки могут вызываться внутренними натяжениями, обусловленными неправильностью роста кристалла, а также искажениями вследствие присутствия посторонних атомов. Для искажений этого рода характерна их статич. природа— они являются неподвижными, и обусловленное ими сопротивление не зависит от t°. Такого рода «остаточное сопротивление» действительно на опыте наблюдается. Рассеяние электронов на искажениях статического характера не может сопровождаться обменом энергии. Отсюда вытекает, что это добавочное сопротивление при расчете джоулева тепла во внимание приниматься не должно.

Изложенная теория является неполной. Ф-ла (4) показывает, что сопротивление исчезает только при абсолютном нуле, между тем, как известно, у многих веществ наблюдается t°_Kpum. (обычно порядка нескольких абсолютных градусов), ниже которой сопротивление равно нулю. Тело переходит в состояние сверхпроводимости (смотрите). До сих пор построить строгую количественную теорию этого явления не удалось. Многократно высказывались предположения, что для объяснения этого явления необходимо учесть взаимодействие между электронами, которое до сих пор теорией во внимание не принималось. Недавно Френкель развил качественную теорию сверхпроводимости, в которой выясняется решающая роль взаимодействия между электронами, для объяснения явления сверхпроводимости. Недостатки другого рода современной теории металлов связаны слишком схематич. учетом структуры самого металла. Так, до сих пор еще нет удовлетворительной теории, объясняющей зависимость электропроводности от давления (эффект Бриджмена).

2. Электронные полупроводники. Существенным результатом квантовой теории является то обстоятельство, что механич. система может иметь не любые значения энергии, а только ряд дозволенных энергетич. уровней, которые образуют иногда дискретный ряд, иногда — сплошной, иногда — смешанный. Для системы электронов в кристаллич. решетке характерно распадение дозволенных энергетических уровней на ряд дискретных «полос» (фигура 3), внутри которых они образуют практически сплошной спектр. Ширина этих полос, а также ширина «запретных» зон зависит от двух факторов: от системы дозволенных уровней в изолированных атомах данного вещества и от кристаллической структуры твердого тела, образованного из этих атомов. Система является настолько сложной, что заранее предвычислить величины этих уровней и их взаимное расположение оказывается совершенно невозможным. Однако можно все же высказать ряд общих соображений. Можно например показать, что чем прочнее электроны в решетке связаны с атомами, тем уже полосы и тем шире запретные зоны. Возможны и такие случаи, когда полосы налегают друг на друга. Эти общие соображения имеют большое значение, если принять во внимание эмпирич. закон, известный под именем принципа Паули: на одном и том же энергетич. уровне может находиться не больше двух электронов данной системы. Этот закон является как бы коррективом к столь же общему принципу минимума энергии, ссгласно которому механич. система в устойчивом состоянии (движения или равновесия) должна обладать минимумом энергии. Без принципа Паули этот закон приводил бы к тому, что в «нормальном» состоянии все электроны находились бы на самом нижнем уровне первой полосы. С учетом принципа Паули он приводит к тому, что электроны располагаются последовательно, начиная с самого нижнего по два на каждом уровне, т. ч. в этом случае минимальное возможное значение полной энергии будет больше, чем в первом случае.

Предположим теперь, что число электронов в нашей решетке в точности равно удвоенному числу уровней в первой полосе (практически, всегда приходится иметь дело с первыми двумя полосами) и что «зазор» между первой и второй полосами довольно велик. При наложении электрического поля электроны будут ускоряться и переходить с одного уровня на другой. Но т. к. все уровни первой полосы уже заняты, а вторая полоса находится слишком далеко и недостаточно сильное поле не в состоянии перебросить туда электроны, электрич. тока в таком теле очевидно быть не может: тело является диэлектриком. Т. о. мы видим, что свойства вещества быть проводником или диэлектриком определяются не столь прочностью связи электронов с атомами, как соотношением между числом уровней в полосе и числом электронов. Конечно первый фактор играет также роль, поскольку, как было указано, более прочной связи соответствуют более узкие полосы, а следовательно более широкие запретные зоны. В мет возможны разные случаи. Напр. в случае щелочных металлов верхняя половина первой полосы оказывается свободной; в случае щелочноземельных — вся первая полоса занята, но вторая налегает на первую, т. ч. поле в состоянии перебрасывать туда электроны. Переходя к электронным полупроводникам, мы можем определить их как такие вещества, которые являются при абсолютном нуле идеальными диэлектриками, но у которых зазор между первой и второй полосами настолько невелик, что тепловое движение, начиная с известной t°, уже в состоянии перебрасывать в верхнюю полосу электроны. Тогда электропроводность такого вещества будет обусловливаться наличием свободных мест в первой полосе и присутствием электронов во второй. В отношении механизма электропроводности для полупроводников остается справедливым все сказанное относительно металлов, хотя внешне будут проявляться другие закономерности. Так как электропроводность σ естественно пропорциональна числу принимающих участие в движении электронов, полупроводники будут характеризоваться чрезвычайно малой по сравнению с металлами уд. электропроводностью. В случае металлов число участвующих в проводимости электронов не зависело от t° и потому в ф-лах (3) и (4) ohq было включено в Const. Здесь же, т. к. перебрасывание электронов во вторую полосу обусловлено тепловым движением решетки, число электронов проводимости существенно зависит от

_ AW

t° оно пропорционально e ^2кг, где ΔW—ширина запретной зоны, к—постоянная Больцмана. Тогда зависимость электропроводности от t° будет выражаться ф-лой:

2hT

о=Const ---, (5)

τ^α

где α—небольшое число. Отсюда видно, что уд. электропроводность в противоположность тому, что мы имеем в мет, будет (до известного предела) расти с t°. Это действительно экспериментальйо и наблюдается у полупроводников. Полупроводники такого типа согласно введенной Фаулером терминологии называются истинными. Существуют однако, вещества, которые сами по себе не являются полупроводниками, т. к. у них зазор между по

а б Фигура 3. Фигура 4.

лосами слишком велик. Однако в этих вещест-вах могут иметься примеси, которые обладают уровнем, лежащим внутри запретной зоны. При этом возможны два следующих случая: 1) атомы примеси имеют свободный уровень, который лежит вблизи верхней границы первой полосы; 2) уровень атома занят, но он лежит вблизи нижней границы второй полосы (фигура 4, а и б). В обоих этих случаях мы имеем полупроводники, хотя они и отличаются несколько по своим свойствам.

3. Твердые электролиты. Переходя к веществам с ионной проводимостью, нужно заметить, что вследствие большой массы ионов (по сравнению с массой электронов) движение ионов как целых может изучаться методами обычной механики. В частности в случае твердых электролитов встает вопрос о возможности’и характере движения ионов в кристал-лич. решетке. Физич. картина движения ионов в гетерополярной кристаллич. решетке дана в 1926 году Френкелем и развита в самое последнее время Постом. Совершая тепловое движение, ионы колеблются возле своих положений равновесия в узлах решетки. Вследствие хаотич. характера этих колебаний в каком-нибудь месте может произойти флуктуация энергии, в результате которой ион может вылететь из своего положения равновесия в «междуионное» пространство. Т. к. в междуионном пространстве имеются локальные минимумы энергии (хотя и более высокие, чем нормальные), ион может застрять в такой «яме»; на месте же нормального положения иона будет «дырка», которая будет вести себя, как заряд знака, противоположного знаку вырванного иона. Колеблясь около нового иррегулярного положения равновесия, ион может перейти в соседнее иррегулярное и т. д. Так к 1к такие переходы обусловлены флуктуациями энергии, то на основании самых общих соображений статистической механики можно показать, что вероятность такого перехода, а следовательно и число диссоциированных ионов пропорциональны

__и_

А-е ^скт,

где А—слабо зависящая от Г величина, Ό— работа перехода иона из нормального в иррегулярное положение, е—основание натуральных логарифмов. При наложении электрич. поля могут иметь место два процесса: 1) диссоциированные ионы под действием электрич. поля будут перемещаться из одного иррегулярного положения в соседнее преимущественно в одном направлении; 2) ионы, колеблющиеся около соседних нормальных положений равновесия, могут переходить в образовавшуюся дырку, причем этот процесс также будет происходить преимущественно в одном направлении. Последний процесс Френкель рассматривает как движение дырки в направтении, обратном движению ионов. Вероятности таких переходов также определяются выражениями приведенного вида, откуда следует, что и электропроводность будет иметь вид

__w

α= Const · e (6)

тот же, что и для электронных полупроводников. Такая темп-рная зависимость действительно наблюдается на опыте. Эта теория объясняет чрезвычайно существенный факт, что очень часто ток в кристалле обусловливается движением только какого-нибудь одного сорта ионов, чаще всего положительных. Раньше это объясняли исключительно размерами ионов, исходя из геометрич. соображений. Однако такое объяснение не совсем удовлетворительно, т. к. выход иона из нормального положения связан с такими искажениями решетки, что геометрич. препятствия для движения больших ионов не окажутся значительными. Кроме того маленькие ионы прочнее связаны с нормальными положениями равновесия. С точки зрения изложенной теории, как показал Пост, это объясняется тем, что маленькие ионы сильнее поляризуют кристалл, вследствие чего работа перехода иона уменьшается, а его вероятность, а следовательно и электропроводность возрастают.

4. Жидкие электролиты являются наиболее типичными ионными проводниками. Это—одна из наиболее исследованных областей с экспериментальной стороны, а некоторые вопросы также достаточно хорошо разработаны и теоретически. В дальнейшем для наглядности под жидкими электролитами понимаются водные растворы солей. В жидкостях движение ионов уподобляется движению обычных м кроскопич. шаров в вязких жидкостях, причем ~т. к. вследствие трения ион под влиян ем электрич. поля движется равномерно, то электропроводность растворов р. основном определяется некоторой средней скоростью движения ионов, т. н. подвижностью, определяемой равенством:

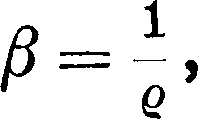
где о—коэф. трения иона, который удовлетворяет ур-ию е. Е=ρ · и;

здесь е—заряд иона, Е—приложенное поле, и—скорость движения иона при данном поле. Существенными факторами, влияющими на подвижность ионов, являются следующие три: структура самого растворителя, взаимодействие ионов с молекулами растворителя, взаимодействие ионов между собой. Роль первого фактора обусловлена тем, что от структуры жидкости зависит ее вязкость, а следовательно и подвижность ионов. Тут гл. обр. имеет значение то обстоятельство, что многие жидкости, в частности вода, построены не из отдельных молекул, а из больших комплексов молекул, согласно взглядам некоторых современных исследователей даже из микрокристалликов, что, во-первых, сильно увеличивает вязкость, а, во-вторых, делает растворитель чрезвычайно чувствительным к изменению тех или других фи-зическ×условий. Влияние второго фактора сводится гл. обр. к электростатич. взаимодействию ионов с молекулами растворителя, к-рое приобретает особенно большое значение в том случае, когда растворитель, как это например имеет место у воды, является полярным—его молекулы обладают дипольным моментом. В этом случае играет большую роль гидратация ионов—б. или м. прочное связывание молекул воды с ионами. Гидратированные ионы имеют больший радиус и следовательно обладают * большим коэф-том трения и меньшей подвижностью. Как правило размеры гидратной оболочки тем больше, чем меньше размеры иона, потому что маленький ион может удержать около себя благодаря более интенсивному полю большее число молекул воды. Этим объясняется тот на первый взгляд непонятный факт,

что ион меньшего радиуса обладает меньшей подвижностью, тогда как нормально должно было бы быть наоборот. Гидратация ионов играет большую роль особенно в том отношении, что она также чрезвычайно чувствительна к различного рода изменениям физич. условий, в частности к изменениям концентрации ионов в растворе, и делает благодаря этому и электропроводность чувствительной к тем же изменениям условий. Экспериментальное изучение эффекта гидратации чрезвычайно затруднено невозможностью отделить его от эффекта ассоциации или полимеризации жидкости, так как все это тесно связано между собой. Теоретические пути для исследования этих вопросов только намечаются.

Макс Борн указал и теоретически разработал еще один эффект взаимодействия ионов с молекулами растворителя. Если непосредственно прилежащие к иону молекулы растворителя прочно с ним связываются, то взаимодействие с более удаленными сводится к ориентации их дипольных моментов по направлению поля. Т. о. вокруг иона вода поляризована. При движении иона поляризация воды не сразу исчезает в том месте, откуда только что ушел ион, а по истечении известного промежутка времени (времени релаксации), которое зависит от вязкости жидкости. Вследствие этого возникает дополнительное поле, противодействующее движению иона, то есть уменьшается его подвижность. Следует отметить, что все более и более выясняется необходимость учитывать в вопросах взаимодействия ионов с растворителем, кроме чисто электростатич. сил, также и химизм .явлений. Однако теория химич. сил еще недостаточно разработана, чтобы ее прилагать к таким сложным системам. Наиболее разработан теоретически (для малых концентраций) вопрос о влиянии взаимодействия ионов на электропроводность. Теория этого эффекта в настоящее время с исчерпывающей полнотой разработана Онзагером на основании физич. представлений, высказанных сперва Дебаем и Гюк-келем (в последние годы Дебаем и Фалькенга-геном). Еще с 1923 г. Дебай и Гюккель показали, что вокруг какого-нибудь иона создается всегда «ионная атмосфера», образованная главным образом ионами противоположного знака. Это нужно понимать так, что если мы сосредоточим наше внимание на каком-нибудь, скажем, положительном ионе и будем наблюдать за проходящими мимо него ионами, то в среднем мимо него будет проходить больше отрицательных ионов, чем положительных. Если избранный нами ион неподвижен, то ионная атмосфера будет обладать сферической симметрией. При наложении электрич. поля будут иметь место два процесса. Прежде всего будет релаксационный эффект, аналогичный борцовскому эффекту в случае взаимодействия с растворителем. В самом деле при перемещении иона в течение промежутка времени, меньшего времени релаксации (то есть практически времени исчезновения старой или времени создания новой) ионной атмосферы, оставшаяся позади него атмосфера еще не исчезнет и, так как в ней имеется излишек отрицательного заряда, она будет притягивать ион назад, тогда как впереди ионная атмосфера еще не успеет достроиться, и ион будет встречать излишек (по сравнению со статическим случаем) положительных ионов. Они будут его отталкивать обратно. В результате эта асимметрия ионной атмосфе ры приведет к уменьшению подвижности иона. Далее будет иметь место чисто электрокинетич. эффект, известный под именем электрофореза, к-рый обусловлен тем обстоятельством, что окружающие избранный ион заряды противоположного знака под действием электрич. поля двигаются в обратном направлении, увлекая при этом с собой и воду. Т. о. наш ион как бы движется не в покоящейся воде, а в идущем навстречу ему потоке. Это является дополнительным фактором, уменьшающим подвижность ионов. Математич. развитие этих идей приводит к следующей зависимости электропроводности от концентрации:

α= а + b ]/с

(а и Ь—постоянные, с—концентрация), известной из опыта под именем закона К о л ь р ау-ш а. Помимо этого дебаевские представления о ионной атмосфере нашли непосредственное подтверждение в ряде специфич. явлений, связанных с релаксационными свойствами ионной атмосферы. Так например, можно ожидать, что при очень сильных полях, когда ион за время, меньшее времени релаксации, успевает выйти за пределы ионной атмосферы, ее тормозящее действие не будет сказываться. Этот эффект, проявляющийся следовательно в увеличении подвижности ионов в случае очень сильных полей, действительно наблюдался Вином. Кроме того имеются специфич. эффекты в случае наложения переменных полей. Напр. при переменных полях с периодом, меньшим времени релаксации, также будет исчезать тормозящее действие ионной атмосферы. Так как мы представляем себе ионную атмосферу покоящейся, то она действует тормозяще при уходе иона и в такой же степени ускоряюще при его возвращении к прежнему месту. Необходимо однако отметить, что в области больших концентраций теория встретила пока непревзойденные трудности, связанные с необходимостью учитывать более субтильную его структуру, а не характеризовать его только зарядом. В этой области должна войти в свои права квантовая механика.

5. Прохождение электричества через газы. Электропроводность газов объясняется присутствием ионов или электронов в газах, которые обычно создаются либо какими-нибудь внешними агентами (свет, рентгеновы лучи, катодные лучи и тому подобное.) либо вследствие теплового движения. Практически в газах всегда имеются заряды. Ионы и электроны в газах могут двигаться свободно, и все особенности, наблюдающиеся при электрических разрядах в газах, обусловливаются лишь взаимодействием самих ионов (смотрите Разряд электрический). Характер электрического разряда будет определяться двумя факторами—объёмными зарядами и рекомбинацией ионов. Образование объёмных зарядов определяется распределением скоростей ионов, внутренним полем, рекомбинацией ионов. В свою очередь они определяют распределение потенциала в разрядной трубце. Рекомбинация ионов определяется тем полем, в к-ром ионы двигаются, и их индивидуальными свойствами. Типичная зависимость силы тока в газе от напряжения приведена на фигуре 5. Первый. участок кривой, соответствующий линейному

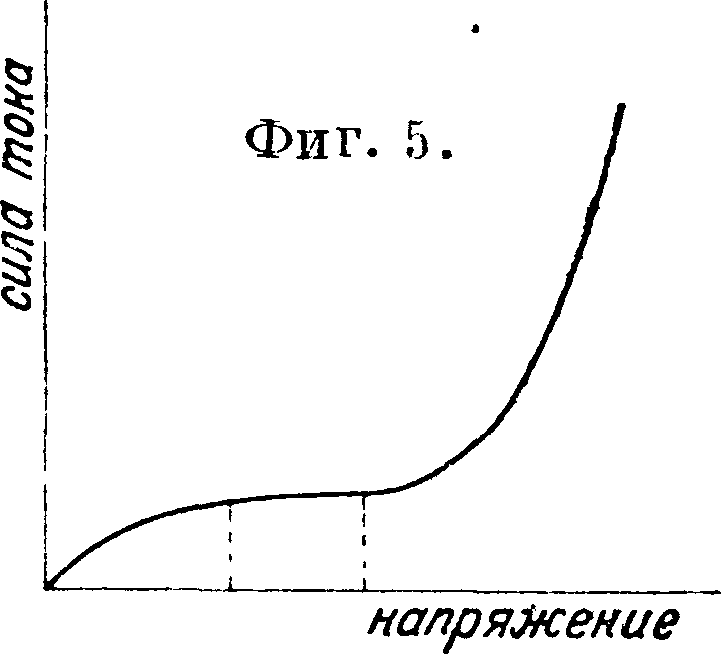
росту тока с напряжением (в согласии с законом Ома), объясняется возрастанием скорости ионов с напряжением. В этом случае число рекомбинирующих ионов чрезвычайно велико. Второй участок кривой, соответствующий току насыщения, объясняется тем, что число создающихся в газе ионов в точности компенсируется числом рекомбинирующих. Дальнейший подъем кривой связан с возникновением ударной ионизации, приводящей к лавинообразному току и к пробою (смотрите).

Лит.: Д а р р о у В., Статистическая физика и электронная теория металлов, пер. с англ., М.—Л., 1933; Вальтер А. и др., Физика диэлектриков, М.—Л., 1932; Самойлов и ч А., Природа электрического сопротивления металлов, «Электричество», М., 1931, 18; Арсеньева А. и Бронштейн М., Физические свойства электронных полупроводников, «Журнал технической физики», М., 1932, т. 2, стр. 919; Комптон К. и Л э н г м ю р И., Электрические разряды в газах, «УФН», 1931, т. M, вып. 1 и 2; Brillouin L·., Die Quaiiten-statistik u.ihre Anwendung auf die Elektronentheorie d. Metalle, B., 1931; Falkenbagen H., Elektrolyte, Lpz., 1932; P e i e г 1 s R., Elektronentheorie d. Metalle, «Ergebnisse d. exakten Naturwissenscliaften», B., 1932, B. 11, p. 265; Frenkel J., Zur wellenmechanischen Theorie d. metallischen Leitfahigkeit, «Ztschr. fur Physik», B., 1928, B. 47, p. 819; F r e n k e 1 J., On the Possible Explantation of Superconductivity, «The Physical Review», L., 1933, v. 43, p. 907; Fowler R., Report on the Theory of Semi-Conductors, «Physikalische Ztschr. d. Sowjetunion», 1933, B. 3, p. 487; Fowler R., Elementary Theory of Semi-Conductors, «Proceedings of the Royal Society», L., 1933, v. 140, p. 503; J о s t W., Diffusion a. Electrolytic Conduction in Solids, «Journal of Chemical Physics», 1933, v. 1, p. 466; Onsager a. Fuoss, Irreversible Processes in Electrolytes, «Journal of Physical Chemistry», N. λ⁷., 1933, v. 36, p. 2689. А. Самойлович.