> Техника, страница 97 > Электричество

Электричество

Электричество. Под словом Э. понимается как электрич. заряд, так и в более широком смысле вся совокупность электрических явлений, в которых проявляются существование, движение и взаимодействие электрич. зарядов. Явления эти столь многообразны и универсальны, что краткая характеристика их представляется весьма затруднительной. Самое содержание, вкладываемое в термин Э., испытывало в процессе развития физики и техники весьма глубокие изменения.

Значительная часть учения об Э. может быть изложена вне связи с вопросами о природе электрона и электромагнитного поля. Ограничиваясь в дальнейшем кратким изложением основ до-квантовой теории электричества, мы не совершим значительных погрешностей против истины в кругу тех вопросов, которые этой теорией рассматриваются. Хотя в дальнейшем мы и будем рассматривать электрон как корпускулу, отвлекаясь от его волновой природы, однако результаты такого рассмотрения в пределах намеченного круга вопросов почти. полностью совпадают с результатами последовательного применения квантовой механики. См. Атом (Доп. том), Кванты, Механика квантовая, Электрон.

I. Основные гаконы теории Э. в отсутствии диэлектриков и магнетиков. Силы, действующие на заряды. Напряженность электромагнитного поля. Основной закон электростатики, открытый Кулоном (1785 г.), в современной формулировке гласит, что два находящихся в вакууме неподвижных электрич. заряда q₁ и q₂, размеры которых достаточно малы по сравнению с их взаимным расстоянием R (т. н. «точечные» заряды), действуют друг на друга с равными и противоположными силами притяжения или от-

талкивания, прямо пропорциональными д_г и q₂и обратно пропорциональными квадрату R:

(1)

Значение коэф-та пропорциональности к определяется выбором единицы количества Э. (заряда). В т. наз. абсолютной электрич. системе единиц (системе CGSE), соответствующей значению к=1, единицей количества Э. будет заряд, действующий на равный ему заряд, помещенный на расстоянии R — 1 см, с силой F=1 дине. В практической системе единиц употребляется в качестве единицы количества электричества 1 кулон, или 1 ампер/ск.=3 · 10⁹ абс. ед. В силе F, действие которой испытывает данный заряд со стороны всякого другого заряда или любой их совокупности, проявляется поле, создаваемое этими зарядами. В случае неподвижных зарядов это поле является чисто электрическим (элект-ростатич. поле); количественной характеристикой его является его напряженность Е, равная по определению (по величине и направлению) в каждой точке пространства той силе, какую испытывает помещенный в эту точку заряд q=1 абс. ед. Ясно, что при этом геометрич. размеры q должен быть настолько малы, чтобы в занимаемом им объёме можно было считать Е постоянным. Сила же, действующая на такой «точечный» заряд q произвольной величины и знака, будет

F=qE. (2)

Из сравнения (2) с законом Кулона (1) при к=1 следует, что если поле создается «точечным» зарядом q, то есть зарядом, размерами которого можно пренебречь по сравнению с расстоянием R от этого заряда до рассматриваемых точек поля, то в произвольной точке, удаленной от него на расстояние R, напряженность Е численно равна

Так как вектор Е направлен по направлению радиуса-вектора R, проведенного из q в рассматриваемую точку поля, если q > 0, и направлен в противоположную сторону, если q < 0, то окончательно

£=#*·#’ <^3а)

О

ибо численная величина вектора равна единице. В случае произвольной системы зарядов необходимо мысленно разбить эти заряды на достаточно малые по геометрическим размерам элементы (точечные заряды). Тогда напряженность результирующего поля всей системы выразится векторной суммой напряженности полей (За), возбуждаемых каждым отдельным ее элементом. Как уже указывалось, при своем движении электрические. заряды возбуждают не только электрическое, но и магнитное поле. Другими словами, магнитные свойства суть такой же первичный признак электрического заряда, как и электрические; реальные поля, создаваемые зарядами, суть поля электромагнитные, и только в особых частных случаях поле зарядов выступает как «чисто электрическое» или «чисто магнитное» поле. Отложив пока вопрос о том, каково магнитное поле движущегося заряда, остановимся на том, какая сила действует в заданном магнитном поле на движущиеся в нем заряды.

Чтобы полностью охарактеризовать магнитное поле, нужно задать величину и направление так называемым вектора напряженности магнитного поля

Я в каждой точке этого поля. Сила, действующая в поле Я на заряд q (перпендикулярная к Я и к скорости заряда ®), направлена так, что образует с Я и v правовинтовую систему (говорят, что вектор F образует с векторами Я и V правовинтовую систему, если при повороте ручки буравчика от Я к v острие его ввинчивается в сторону направления вектора F) и численно равна

F=~ ©Яsin а, (4)

где а—угол между v и Я (фигура 1), а с—постоянный коэф., так называемым электродинамическая постоянная. Численное значение этой постоянной зависит от выбора системы единиц. Если измерять все величины (в том числе и электрич. заряд q) в абсолютной электромагнитной системе единиц, то численное значение коэф-та с равно скорости света ^3 · 10¹⁰ см/ск.

В векторных обозначениях все сказанное о силе может быть записано одной ф-лой:

F=^[vHl (4а)

где прямые скобки означают векторное произведение (смотрите Векторное исчисление). Существенно здесь то, что неподвижный заряд никакой силы в магнитном поле не испытывает, что и дает возможность установить различие между действием на заряд поля электрического и поля магнитного. Далее существенно, что сила F перпендикулярна к скорости заряда, а поэтому изменяет лишь направление, но не численную величину его скорости. Другими словами, силы магнитного поля при движении зарядов непосредственно никакой работы не совершают. Общая сила, действующая на «точечный» заряд q, движущийся со скоростью v в электромагнитном поле, характеризующемся напряженностями £ и Я, слагается из сил (2) и (4а):

F=g{E + ±[vH]). (5)

Эта формула была дана Лоренцем, именем которого обычно называют и силу F (Лоренце, ва сила). Она дает возможность с помощью законов механики определить движение электрич. зарядов и т. о. лежит в основе динамики электронов и протонов.

Электрический ток и закон сохранения Э. Сила электрического тока 1 по определению равна заряду, переносимому в единицу времени через сечение тока движущимися элементарными частицами (электронами, ионами и т. д.). Единице силы тока соответствует протекание единицы заряда в секунду. В практической системе единиц единицей силы тока яв

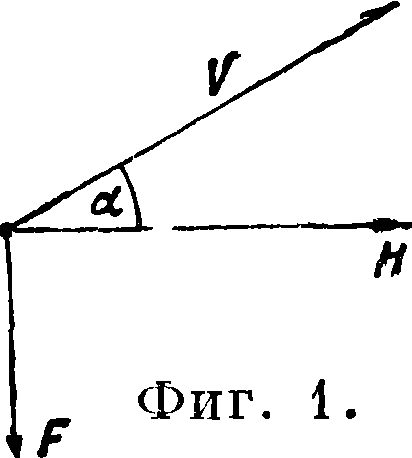
ляется ампер:

1А=lC/ск.

Заряд, переносимый в единицу времени через единицу площади сечения тока, называется плотностью тока и обозначается буквой j:

J ⁼ ~s ’

_где s — сечение тока. Однако если ток неоднороден, то есть неравномерно распределен по сечению S, то плотность тока j будет различной в различных точках сечения тока. Чтобы определить ее значение в данной точке, нужно разделить силу тока di, протекающего через прилегающий к этой точке бесконечно малый элемент сечения тока, на площадь этого сечения dS

J-Ж <^to>

Обычно плотность тока j считают вектором, направление которого в каждой точке совпадает с направлением тока. При этом направление тока совершенно условно считается совпадающим с тем направлением, в к-ром должны были бы двигаться положительные заряды. В силу меньшей своей массы электроны гораздо более подвижны, чем протоны, и поэтому в большинстве случаев эЛектрич. ток обусловлен движением именно электронов. В этих случаях приходится считать ток «текущим» в сторону, обратную действительному направлению движения отрицательных зарядов. Итак, количество Э., протекающего в единицу времени через элемент сечения тока dS, равно di=j dS; при этом предполагается, что элемент сечения тока dS перпендикулярен направлению тока. Если же площадка dS не перпендикулярна току, то количество протекающего через нее Э. определится ф-лой

di=j cos (j, n) dS=j_n dS, (7)

где n — направление нормали к площадке dS, a j_n — нормальная слагающая плотности ток% j. При этом силу тока di нужно считать положительной или отрицательной в зависимости от знака cos (j, я), то есть в зависимости от того, протекает ли ток через площадку dS в направлении нормали или в обратном направлении.

Рассмотрим теперь произвольную поверхность

S. Общее количество протекающего через нее Э. определится очевидно суммой или, что в сущности то же, интегралом выражений (7), взятым по всём ее элементам:

2 i«^dS =//я dS. (7а)

S

Если эта поверхность S замкнута (как например поверхность шара), то сумма эта будет очевидно равна общему количеству Э., выходящему за единицу времени из ограниченного поверхностью S объёма V (если п есть внешняя нормаль к поверхности). С другой стороны, согласно одному из основных постулатов теории Э. не может ни возникать ни исчезать. Следовательно количество Э., вышедшего за 1 ск. за пределы объёма F, должно равняться убыли — за тот же период времени заряда q_y находящегося внутри объёма V. Иными словами

(j)in ^dS= ~μ· (⁸)

[Кружок у знака интеграла должен означать, что интеграл берется по замкнутой поверхности (или в дальнейшем по замкнутой линии)]. Это весьма важное уравнение называется уравнением непрерывности и является математическим выражением постулата с о-хранения количества Э. В случае постоянных токов распределение зарядов не меняется со временем, то есть ~=0, и стало быть и левая часть ф-лы (8) тоже равна нулю. Это значит, что положительные члены интеграла или суммы (7а) в этом случае компенсируются отрицательными, то есть что если через одну часть поверхности S Э. вытекает наружу, то через другую ее часть поступает внутрь равное количество Э. Легко сообразить, что в случае постоянного тока, протекающего по неимеющему разветвления проводнику, через любое сечение проводника протекает ток одинаковой силы: в противном случае в нек-рых участках проводника должно было бы происходить постепенное накопление зарядов и ток не был бы постоянным. Именно поэтому можно говорить просто о силе постоянного тока, не указывая о каком именно сечении тока идет речь. По той же причине постоянные токи всегда замкнуты, ибо в противном случае у концов тока происходило бы накопление зарядов.

Заряд q, заключенный внутри произвольного объёма У, м. б. выражен через плотность Э. ев этом объёме (то есть через величину заряда ρ, приходящегося в единицу объёма) с помощью ур-ия

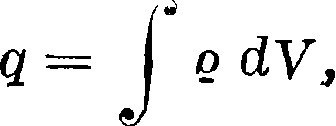
V

ибо ρ dV по определению есть заряд элемента объёма dV. Внося это выражение в формулу (8), получаем несколько измененную форму ур-ия непрерывности:

(j) Ьь dS=- ^ J* e dV. (8а)

Легко наконец найти связь между плотностью тока .? и числом и скоростью элементарных зарядов (электронов, ионов и тому подобное.), образующих своим движением этот ток. Пусть на единицу объёма тока приходится η движущихся элементарных зарядов величины д₀. Предположим сначала, что все эти заряды двигаются с одинаковой скоростью V. В этом случае за единицу времени все они перемещаются на расстоянии ν и стало быть через произвольную площадку dS, перпендикулярную к ν, за единицу времени должны пройти все те и только те заряды, которые находились внутри цилиндра с основанием dS и высотой ν. Объем этого цилиндра равен ν-dS, число находящихся в нем зарядов равно п· г>· dS, и стало быть сила проходящего через dS тока равна di=q₀nv dS,

откуда на основании равенства (6а) получаем • di

О=gg=nq₀v. (9)

Очевидно, что эта формула остается справедливой и в том случае, когда скорости различных зарядов неодинаковы, если только при этом под ν понимать среднюю скорость зарядов. Наконеп если через ρ обозначить объёмную плотность движущихся зарядов

ρ=nqo (10)

и если учесть, что вектор j параллелен вектору ν, то ур-ие (9) примет вид:

j=ρ · ν. (10а)

В рамках макроскопич. теории в этом ур-ии под д и ν нужно понимать среднюю плотность и среднюю скорость движущихся в проводнике зарядов. Однако это ур-ие остается справедливым и при микроскопии, рассмотрении явлений; под д нужно понимать в этом случае истинную плотность зарядов, отличную от нуля лишь, внутри электронов и протонов, а под ν—истинную скорость данного элементарного заряда.

Силы, действующие на токи в магнитном поле. Всякий электрич. ток, помещенный в магнитное поле, испытывает действие механич. силы, равной сумме Лоренцевых сил, действующих на каждый элементарный движущийся заряд. Рассмотрим некоторый элемент тока, то есть элемент объёма тока dV столь малый, что значения величин У и Я можно считать в нем постоянными, но все же еще столь большой, что в нем имеется достаточно большое число элементарных движущихся зарядов

q_Q. На каждый из этих зарядов q₀ действует со стороны магнитного поля сила (4а). Если бы скорость ν всех движущихся в проводнике зарядов была одинакова, то общая сила, действующая на весь элемент dV, была бы равна произведению силы (4а) на число n dV зарядов в этом элементе:

F=n dV ^ · [VH],

где п означает число зарядов, приходящихся на единицу объёма. Хотя фактически различные заряды обладают весьма различными скоростями, все же эта формула остается справедливой, если только под ν понимать среднюю скорость зарядов. Далее произведение nq₀v согласно равенству (9) равно плотности тока /, и значит

F=т VH] dV. (И)

Т, Э. Доп. т.

Зв

Фигура ί

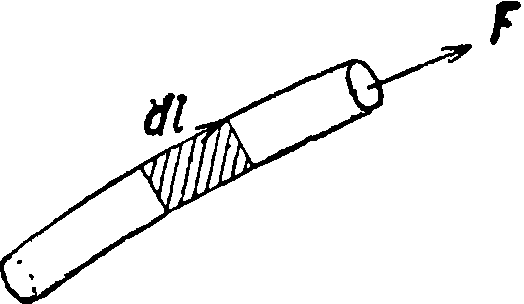
Это выражение легко преобразовать для того случая, когда ток течет по весьма тонкому цилиндрич. проводнику. За элемент тока dV в этом случае можно взять просто небольшой отрезок проводника, как показано на фигуре 2, то есть цилиндр высоты dl с площадью основания dS; в этом случае dV=dl-dS. Если направление dl совпадает с направлением у, то, т. к.=j dS, получаем:

Idl=jdS · dl — j dS · dl=j dV. (12)

Значит сила F, действующая на элемент dl тока I в поле Н, согласно (11) и (12) равна

F=— [dl,H]. (11а)

с

Эта формула выражает собой известный закон Био-Сава р а, ибо содержанке ее согласно смыслу векторного произведения (dl, Н) сводится к следующему: действующая в поле Н на элементы тока I dl сила F перпендикулярна к векторам dl и Н и образует с направлениями этих векторов правовинтовую систему, а по численному значению она равна

F=— IHdl sin (dl, Η), с

Пользуясь ф-лой (И) или (11а), можно полностью определить все силы, действующие в% произвольном магнитном поле на произвольную систему токов, для чего конечно нужно предварительно все эти токи мысленно разложить на совокупность бесконечно-малых элементов dV или I dl. Обратно, с помощью формулы (11а) можно измерить напряженность магнитного поля по силам, действующим в этом поле на элемент тока I dl.

Пусть например цепь тока, образованная толстым твердым проводником, замкнута маленьким отрезком dl очень тонкой и гибкой проволочки. Если по цепи течет ток известной нам силы и если элемент цепи поместить в произвольное магнитное поле Я, то проволочка эта будет изгибаться под действием приложенной к ней силы (11а). Измеряя прогиб проволочки и определяя т. о. величину действующей на нее силы F, можно по формуле (11а) определить напряжен; ность Я в месте нахождения проволочки. Этот способ измерения магнитного поля практически далеко не всегда является наиболее простым и удобным, но принципиально он важен, потому что он непосредственно вытекает из ф-лы (11а). Ведь в сущности можно сказать, что этой именно ф-лой или эквивалентной ей ф-лой (И) определяется самое понятие напряженности магнитного поля. [Речь идет о поле макроскопическом. При более детальном микроскопическом рассмотрении нужно учесть как атомистическое строение Э., так и изменения магнитного поля, испытываемые им внутри проводников на расстояниях атомарного порядка величины, причем вместо ф-лы (11) необходимо непосредственно пользоваться исходной ф-лой (4а).]

Магнитное поле токов. Измерения магнитного поля токов повели к установлению следующих закономерностей. Магнитные силовые линии поля, возбуждаемого произвольным элементом тока I dl (или j dV), представляют собой систему окружностей, нанизанных на прямую, проходящую через элемент тока dl. Направление этих силовых линий образует правовинтовую систему с направлением dl или j. Численная величина напряженности Я обратно пропорциональна квадрату расстояния R рассматриваемой точки поля от элемента I dl (или JdV) и кроме того пропорциональна синусу угла между проведенными из I dl радиусом-вектором R и направлением dl или j. Все эти свойства в обозначениях векторного исчисления выражаются ф-лой

Я

[№

dV =

^r dlR]

cm

(13)

Напряженность же магнитного поля произвольной системы токов равна векторной сумме напряженностей полей, возбуждаемых каждым элементом этой системы. Выполняя это суммирование, можно например показать, что напряженность поля бесконечного прямого тока силы I на расстоянии R от него равна

Я =

21

cR

(14)

Нужно однако заметить, что в рамках учения о постоянных токах формула (13) не м. б. подвергнута непосредственной проверке, ибо постоянный ток всегда замкнут, и поэтому никогда нельзя изолировать какой-либо один его элемент I dl. Поскольку же изучаются поля, получающиеся в результате наложения полей многих отдельных элементов тока, постольку можно предложить и другие выражения для поля отдельного элемента тока, приводящие к тем же окончательным результатам для результирующего поля замкнутых токов; такова например формула Ампера для поля отдельного элемента тока, существенно отличающаяся от ф-лы (13). Однако изучение поля токов переменных, далеко не всегда являющихся замкнутыми, однозначно решает вопрос в пользу ф-лы (13).

Постоянные электрич. и магнитное поля произвольной системы неподвижных зарядов и постоянных токов однозначно определяются ф-лами (За) и (13). Однако эти формулы нельзя непосредственно обобщать на случай переменных электромагнитных полей, ибо они носят в сущности характер законов дальнодействия, непосредственно выражая напряженности поля Е и Н в произвольной точке поля как функцию расстояния этой точки от удаленных от нее зарядов и токов. Помимо того и в случае постоянных полей непосредственное пользование ф-лами (За) и (13) не всегда является удобным и целесообразным. Поэтому для дальнейших обобщений необходимо преобразовать эти ф-лы и рассмотреть ряд вытекающих из них следствий.

Работа электрических сил. Потенциал. Работа, совершаемая силами электрич. поля при перемещении заряда q на отрезок dl, равна

F cos (E, dl) dl — qE cos (E, dl) dl — дЕ_г dl.

В частности работа А при перемещении на расстояние dl единичного положительного заряда равна

А =Е_г dl.

Работа, совершаемая при перемещении единичного положительного заряда по конечному пути L, равна

А=J E, dl,

L

Фиг. где знак L у интеграла означает, что необходимо вычислить сумму значений подинтегрального выражения для всех элементов линии L. Эту операцию называют интегрированием по линии L.

В частности работа электрических сил поля элементарного (точечного) заряда q, совершаемая при перемещении на dl пробного единичного положительного заряда, согласно (За) равна

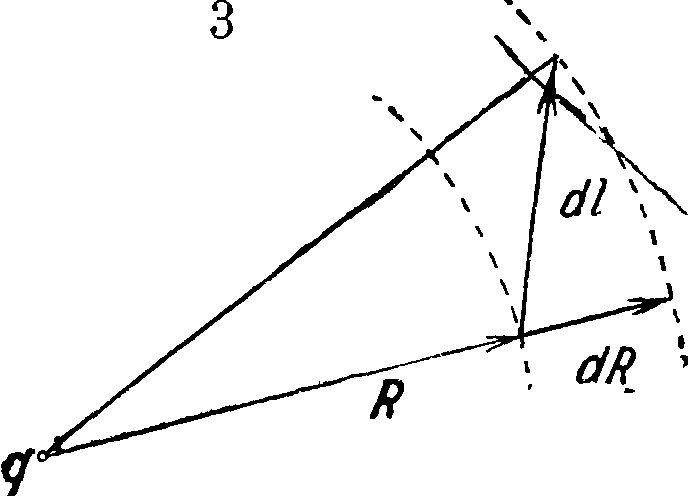
А=Е_г dl=A. cos (R, dl) dl=-i dR, (15)

где dR есть проекция перемещения пробного заряда dl на проведенный из возбуждающего поле заряда q радиус-вектор R (фигура 3). Как видно из фигуры, dR есть вместе с тем приращение численного значения радиуса-вектора R, то есть увеличение расстояния пробного заряда от заряда q. Следовательно и работа, совершаемая при перемещении пробного заряда по произвольному конечному пути L, также будет зависеть лишь от того, как при этом перемещении изменяется расстояние пробного г“ заряда от заряда q, то есть будет зависеть только от положения начальной и конечной точек пути L, но не от формы этого пути. Так например, работа электрич. сил на пути L_x (фигура 4) равна их работе на пути L: избыточная работа, совершаемая на пути L_x при перемещении пробного заряда за пределы сфер радиуса R₂, компенсируется отрицательной работой, совершаемой при последующем приближении пробного заряда к заряду q на последнем участке пути L_x.

Согласно равенству (15) работа А при перемещении dl м. б. представлена в форме полного диференциала:

где R — численное значение радиуса-вектора /?. Следовательно работа, совершаемая при перемещении еди·* ничното положительного заряда из точки Pi в точку Р% по конечному пути L, равна

"/-"-/HB-fi-l,)·

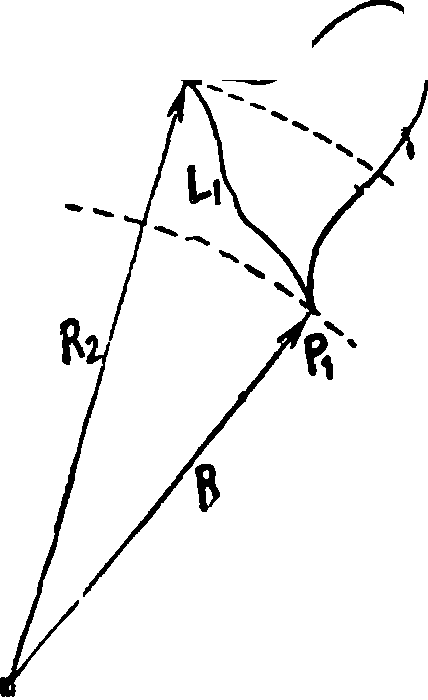
Фигура 4.

где Pi и Й2 — расстояния начальной и конечной точек пути от заряда q. Таким образом работа эта действительно зависит только от положения начальной и конечной точек пути.

Так как поле произвольной системы зарядов можно рассматривать как сумму полей каждого из элементов этих зарядов, то стало быть всякое постоянное электрич. поле обладает этим чрезвычайно важным свойством: работа сил этого поля на произвольном пути между двумя точками зависит только от положения этих точек и вовсе не зависит от формы пути.

Это свойство постоянного электрич. поля дает возможность ввести в рассмотрение чрезвычайно важное понятие о потенциа-л е постоянного электрич. поля. Определение: разность потенциалов между двумя точками постоянного электрического поля равна взятой с обратным знаком работе, совершаемой силами поля при перемещении единичного положительного заряда из первой точки во вторую. Стало быть разность потенциалов άφ между двумя точками, отделерными бесконечно-малым расстоянием dl, равна аφ=— А=— Е_г dl. (16)

Разность же потенциалов <р₂— φ_χ между точками 1 и 2, находящимися на конечном расстоянии друг от Друга, определяется интегралом

2

Ψί — Ψι= — f Ei dl, (16a)

l

причем этот интеграл м. б. взят по любому пути, соединяющему точки 1 и 2. Понятие потенциала (смотрите) играет чрезвычайно важную роль в учении о постоянном электрич. поле, и пользование им чрезвычайно облегчает решение ряда конкретных задач. В частности весьма существенно то, что заданием потенциала как функции точки однозначно определяется и напряженность постоянного электрич. поля в каждой его точке. Т. о. задача изучения векторного поля напряженности Е м. б. сведена к значительно более простой задаче изучения скалярного поля потенциала φ. Независимость работы сил данного поля от формы пути яляется необходимым и достаточным условием для того, чтобы работа сил этого поля на любом замкнутом пути была равна нулю. Действительно, рассмотрим произвольный почти замкнутый путь PMQ (фигура 5). Работа на этом пути должна равняться работе на прямом отрезке PQ, соединяющем Р с Q. При сближении Q с Р отрезок этот обращается в нуль, а путь PMQ становится замкнутым. Т. к. при этом работа на отрезке PQ становится равной нулю, то и работа на замкнутом пути равна нулю. Легко доказать также, что и, обратно, из равенства нулю работы на любом замкнутом пути вытекает независимость работы от формы пути.

Т. о. из доказанного следует, что работа сил постоянного электрич. поля на любом замкнутом пути L равна нулю

(f,E,dl=0, (17)

L

где кружок у знака интеграла отмечает замкнутость пути интегрирования L. Заметим, что линейный интеграл произвольного вектора Е, взятый вдоль какого-либо замкнутого пути L, называется циркуляцией этого вектора вдоль пути L. Т. о. ур-ие (17) сводится к утверждению, что в постоянном электрич. поле циркуляция вектора Е по любому замкнутому пути равна нулю.

Закон Ома. Движущимся в проводнике зарядам (электронам или ионам) приходится преодолевать при своем движении известное сопротивление, обусловленное столкновениями с атомами проводника. При этих столкновениях движущиеся электроны и ионы передают часть своей кинетической энергии атомам проводника, чем и обусловливается его нагревание при прохождении тока. Поэтому постоянный ток может циркулировать в проводнике лишь в том случае, если движение зарядов в нем поддерживается постоянными электрич. силами, действующими на эти заряды. Чем больше эти силы, то есть чем больше напряженность поля Е, тем более сильный ток будет циркулировать в проводнике. Количественно эта зависимость выражается уравнением

j=γΕ, (18)

связывающим плотность тока в каждой точке проводника с напряженностью Е в той же точке. Коэф. γ называется удельной электропроводностью и характеризует собой свойства проводника. Выяснение зависимости γ от атомистической и электронной структуры проводника и от таких факторов, как температура, давление и т. д., является одной из задач электронной теории. Заметим, что величина ρ,

обратная γ (ρ — -ί-)» носит название удельного сопротивления проводника. Уравнение (18) является диференциальной формой известного закона Ома. Для случая однородного цилиндрич. проводника это уравнение легко преобразовать так, чтобы получить закон Ома в его интегральной форме, чаще применяющейся в электротехнике. Пусть S есть сечение данного отрезка проводника, а I—его длина. Сопротивление R этого отрезка, как известно, равно

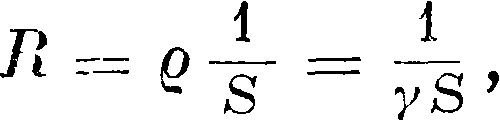
где ρ есть уд. сопротивление проводника. С другой стороны, из равенства (6) и (18) получаем:

1=jS=yS. E.

м

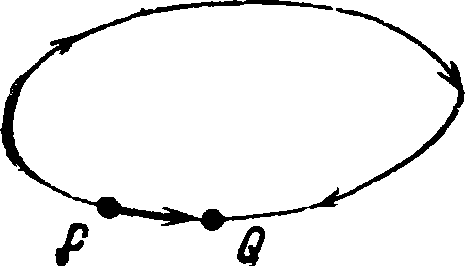
Фигура 5.

Исключая из этих ур-ий yS, получаем

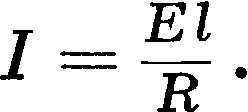
Если напряженность Е меняется вдоль отрезка I, то произведение Е · I нужно заменить соответствующим интегралом, взятым по отрезку I от одного его конца (1) до другого конца (2):

2

I=±fE_tdl. (19)

1

Это и есть закон Ома в интегральной форме. В случае постоянного электрич. поля входящий в правую часть интеграл можно выразить с помощью равенства (16а) через разность потенциалов ψχ—ψι на концах отрезка

= (19а)

В отличие от этого ур-ия, ур-ия (19) и (17) остаются справедливыми и для переменных токов.

2

Интеграл ]Е_г dl называется напряжением вдоль отрезка I (не смешивать с напряженностью Е).

Сторонние эдс. Прохождение электрич. тока всегда сопровождается выделением тепла (нагреванием проводников). Если ток постоянен и электрич. поле стационарно, то это выделение тепла не может очевидно идти за счет энергии электрич. поля, по условию остающегося постоянным. Следовательно ток может поддерживаться лишь за счет каких-либо иных источников энергии, энергия которых непрерывно превращается в тепло. Такими источниками тока м. б. например аккумуляторы или гальванич. элементы, прохождение тока через которые сопровождается химич. реакциями, выделяющими необходимое количество энергии, или же термоэлементы, фотоэлементы и тому подобное. В классич. теории Э. для описания действия этих источников тока вводится феноменология, понятие т. наз. сторонних эдс, то есть сил, действующих на электрич. заряды, но не сводящихся к простому ку-лоновому или магнитному их взаимодействию. Наличие в перечисленных источниках тока этих сторонних эдс вызывает накопление положительных зарядов у положительных полюсов аккумуляторов и элементов и отрицательных зарядов у их отрицательных полюсов. Соединение этих полюсов проводником (замыкание цепи тока) дает возможность этим зарядам стекать от одного полюса к другому, причем эдс источника тока непрерывно пополняет убыль зарядов на полюсах и тем поддерживает постоянство тока. Существенная характеристика сторонних эдс состоит в том, что они всегда связаны с физикохимической неоднородностью вещества. Так, в гальванич. элементе или аккумуляторе имеется комбинация различных соприкасающихся между собой металлов и электролитов, в термоэлементе— два спая металлов, находящихся при различных темп-pax, и тому подобное. Понятно, что в конечном счете все эти сторонние эдс сводятся к обычным взаимодействиям зарядов, входящих в состав атомов неоднородных проводников. Соответствующий детальный анализ механизма действия сторонних сил однако весьма сложен и относится к области электронной теории. Невозможность существования постоянных токов в отсутствии сторонних эдс вытекет также непосредственно из ур-ия (17), ибо, с одной стороны, постоянные токи всегда замкнуты, с другой стороны, согласно ур-ию (17) работа кулоновых сил постоянного электрич. поля при полном обходе электрич. зарядом замкнутой цепи тока равна нулю. Стало быть выделяемое током тепло должно доставляться сторонними источниками.

Индукция токов. Совершенно иначе обстоит дело в случае переменных полей. В этом случае токи могут, как известно, циркулировать в проводниках и при отсутствии всяких сторонних эдс, например за счет механич. энергии, затрачиваемой на вращение динамомашины. Стало быть к переменным полям ур-ие (17) не применимо. Опыт учит, что необходимым условием возникновения токов в замкнутом контуре при отсутствии сторонних эдс является либо изменение магнитного поля в окружающем проводник пространстве либо движение проводника в магнитном поле. В последнем случае токи возбуждаются Лоренцевыми силами (4а), действующими на находящиеся в проводнике и движущиеся вместе с ним элементарные заряды. Возбуждение же токов в неподвижных проводниках м. б. объяснено только тем, что изменения магнитного поля возбуждают в окрз^жающем пространстве поле электрическое, которое ур-ию (17) не удовлетворяет и потому может вызывать и поддерживать движение электрических зарядов по замкнутой цепи тока. Как показывает опыт, циркуляция напряженности этого поля по произвольному замкнутому контуру L, ограничивающему площадку S, равна

<j) Щ dl=- 4- i [HS cos (Н_гп)] =

L

= <²⁰>

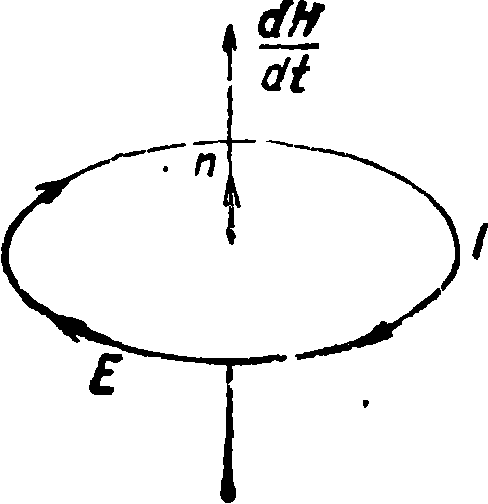
где п — нормаль к площадке S, образующая с направлением обхода контура L правовинтовую систему (фигура 6). Знак минус в этом ур-ии указывает, что например при возникновении магнитного поля, направленного по нормали п, в контуре возникает эдс, равная

(j) E_l dl, направление которой образует с л не право-, а левовинтовую систему (фигура 6); с — электро- Фигура б. динамич. постоянная, впервые встретившаяся нам в ур-ии (4). В том случае, если охватываемая контуром L поверхность настолько велика, что на ее протяжении напряженность поля Н не может уже считаться одинаковой, или же если она настолько изогнута, что в разных ее точках нормаль п к ней имеет существенно различные направления, нужно эту поверхность S разбить на достаточно малые элементы dS и правую часть уравнения (20) заменить суммой или интегралом соответствующих членов для каждого из этих элементов:

i

(20а)

Это ур-ие представляет собой одно из основных уравнений электродинамики, определяющее зайон возбуждения электрического поля изменениями поля магнитного. Оно применимо к любому замкнутому пути интегрирования L вне зависимости от того, проходит ли этот путь по проводникам или по вакууму. Конечно лишь в первом случае возбуждение эдс (|) Е_г dl

будет непосредственно проявляться в возникновении соответствующего тока I, называемого индукционным током. Сила этого тока, индуциро-

ванного в проводящей замкнутой цепи L с сопротивлением R, м. б. определена на основании закона Ома

I=^lR-$E,dl, (21)

из которого на основании равенства (20а) получаем

J_ 1 д_ г“ TJ лп.

¹ cR * Ft.

S

Произведение H_nS, или точнее интеграл JH_n dS, носит название магнитного потока, пронизывающего поверхность S. Термин этот имеет чисто условное значение, ибо конечно ни о каком потоке в механич. или гид-родинамич. смысле этого слова в магнитном поле говорить не приходится. В электротехнике сохранилось кроме того для обозначения этой величины Фарадей-Максвелловский термин: «число магнитных силовых линий, пронизывающих * поверхность S». Дело в том, что эти силовые линии, служащие для графич. характеристики поля, проводятся с таким расчетом, чтобы число их, пронизывающее произвольный элемент поверхности dS, было по возможности равно Н_п dS. Т. о. содержание уравнения (20а) м. б. передано так: эдс индукции, возбуждаемая в произвольном контуре L, равна скорости изменения магнитного потока через охватываемую этим контуром поверхность, деленной на с или же, что то же, скорости изменения числа пронизывающих эту поверхность магнитных силовых линий. Заметим, что всегда можно провести сколько угодно различных, вообще говоря, искривленных поверхностей S, ограниченных одним и тем же контуром L. Однако закон индукции (20а) все же имеет вполне однозначный смысл, ибо, как мы увидим ниже, через любые две поверхности S-l и S₂₎ ограниченные одним и тем же контуром L, всегда проходит одинаковый магнитный поток. В случае постоянного магнитного поля правая часть ур-ия (20а) обращается в нуль и мы получаем в качестве соответствующего частного случая прежнее уравнение (17). Как указывалось, справедливость этого последнего уравнения является необходимым условием возможности введения в рассмотрение элек-трич. потенциала φ. Т. о. в переменных полях обычное понятие электрического потенциала становится неприменимым. Если в электротехнике переменных токов иногда и продолжают пользоваться понятием разности потенциалов, то в сущности под этим термином понимают напряже-2

ние Е_г dl, к-рое взято вдоль некоторого пути между данными точками 1 и 2. Значение этого интеграла в переменном поле именно благодаря нарушению справедливости ур-ия (17) существенно зависит от формы пути переноса заряда (пути интегрирования). Однако на практике часто один из возможных путей переноса заряда (например кратчайший путь, или же путь вдоль проводника, соединяющего точки 1 и 2, и тому подобное.) выделен какой-либо особенностью из числа других, и в электротехнике при оперировании понятием разности потенциалов или напряжения молчаливо подразумевается именно этот путь переноса и близкие к нему. Заметим в заключение, что закон индукции (20а), относящийся к неподвижному контуру, находящемуся в переменном магнитном поле, близко связан с законом индукции токов в проводниках, движущихся в постоянном магнитном поле.

izia)

В этом последнем случае закон индукции непосредственно вытекает из выражения лоренце-вой силы (4а). Пусть данный участок проводника движется в поле Н со скоростью v. Пока в проводнике нет тока, такой же будет очевидно и средняя скорость входящих в состав проводника элементарных зарядов. Стало быть на каждый такой заряд будет в среднем действовать сила (4а-) F= Ц- · [vH].

Такая же сила действовала бы на заряды и в том случае, если бы они находились в эле κι

трич. поле напряженности E=-f [vH]. Стало быть вместо действия поля Н можно рассматривать действие эквивалентного поля Е. Циркуляция напряженности этого поля по контуру замкнутого движущегося проводника L равна

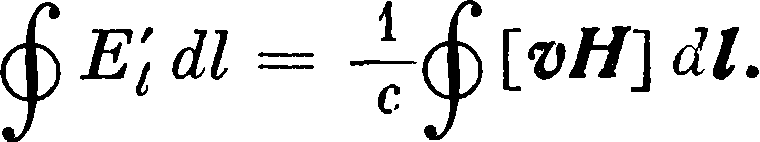
После преобразования можно это ур-ие представить в след, форме:

j₎E_ldl=-^-ijH_n dS. (22)

L S

Это ур-ие весьма аналогично ур-ию (20а), и в правую его часть также входит скорость изменения но времени магнитного потока через поверхность S, охватываемую контуром L. Однако в данном случае это изменение потока вызвано не изменениями напряженности переменного поля //, а перемещением проводника L в постоянном поле Н. Чтобы отметить эту разницу, в ур-ии (22) поставлен знак полной производной по времени а в ур-ии (20а) —

знак частной производной ^-J. Поскольку нас интересует только определение силы индукционного тока в контуре L с помощью ф-лы (21), мы можем не различать между этими двумя случаями индукции и всегда пользоваться ф-лой

(22), понимая под ^- H_ndS полное изменение’

магнитного потока вне зависимости от того, какими именно причинами это изменение вызвав но. Так всегда и поступают в теории переменных токов. С теоретич. же стороны различие между двумя рассмотренными случаями индукции весьма существенно.

Циркуляция магнитного поля. Циркуляция напряженности постоянного элек-трич. поля согласно равенству (17) равна нулю. Совершенно иначе обстоит дело в постоянном магнитном поле. Так например, в поле бесконечного прямого тока магнитные силовые линии представляют собой нанизанные на ось тока окружности. Если в интеграле dl

в качестве пути интегрирования выбрать одну из этих окружностей, например окружность радиуса R, то на всем пути интегрирования Н будет параллельно dl, т. e. H_t=Н, причем численная величина Н также будет оставаться постоянной. Поэтому в этом случае

(£) Hidl=Н · 2nR,

где 2ттR есть длина всей окружности. Внося сюда из (14) значение Н, получаем

= (23)

L

где — сила тока. Существенно, что эта формула справедлива не только для окружности, но и для любого замкнутого контура L, однажды охватывающего ток I. Больше того, исходя из формулы (13), можно доказать, что ур-ие (23) справедливо для любого замкнутого контура в поле произвольной системы постоянных токов, если только под I понимать силу тока, пронизывающего контур L. Это последнее условие можно выразить след. обр. Если S есть какая-либо из поверхностей, ограниченных контуром Z/, то через элемент dS этой поверхности согласно равенству (7) протекает ток силы dl =j_n dS, а через всю поверхность S ток силы

/= (7„ dS.

S

Внося это в формулу (23), получаем

Н_г dl =

= -_с Jin dS.

L S

(23a)

Это уравнение является одним из основных в теории магнитного поля постоянных токов. Из него вытекает в частности невозможность определить скалярный потенциал магнитного поля токов по аналогии с электрич. потенциалом φ. Действительно, однозначное определение этого потенциала, как мы видим, возможно лишь при условии выполнения ур-ия (17), то есть при условии равенства нулю циркуляции электрич. вектора Е. Циркуляция же магнитного вектора Я, вообще говоря, отлична от нуля.

В старых учебниках физики циркуляция вектора Н вдоль контура L определяется как работа, совершаемая магнитным полем при переносе единичного магнитного полюса вдоль контура. Т. к. однако никаких магнитных полюсов в действительности не существует, то циркуляция Н не обладает столь непосредственным физическим смыслом, как циркуляция Е.

Токи смещения. Подобно тому как электрич. поле может возбуждаться не только непосредственно электрическими зарядами, но и изменениями поля магнитного, так и магнитное поле в свою очередь может возбуждаться не только непосредственно электрич. токами, но и изменениями поля электрического. Поэтому в случае переменных полей правая часть ур-ия (23а) должен быть дополнена членом, вполне аналогичным правой части ф-лы (20а):

= к + ^Е« ^dS· <²⁴)

L S S

Сравнивая это уравнение с ур-ием (20а), мы убеждаемся, что в основном эти ур-ия получаются друг из друга заменой электрич. величин на магнитные и обратно. В ур-ие (24) входит кроме того член, зависящий от плотности электрич. тока J, Отсутствие аналогичного члена в (20а) соответствует тому, что никаких магнитных зарядов и магнитных токов, аналогичных электрич. зарядам и токам, не существует. Заслуга введения в ур-ие (24) второго члена принадлежит Максвеллу, к-рый ввел также термин «плотность тока смещения» для обозначения вектора

Jcm.=Tn~dt (²⁵)

С помощью этого обозначения ур-ие (24) можно записать так:

(24а) S

Т. о. можно сказать, что циркуляция магнитного вектора Н определяется плотностью и си лой полного тока, равного сумме электрического тока в собственном смысле слова (так называемым тока проводимости), и тока смещения. Далее, перед аналогичными членами правых частей ур-ий (24) и (20а) стоят разные знаки. Эта разница в знаках означает разницу в направлении индуцированных полей: поле //, возбуждаемое электрическими токами, образует с ними правовинтовую систему, тогда как поле Е, возбуждаемое «магнитными токами смещения» ^, образует с последними систему левовинтовую (фигура 7). Этим в частности обусловливается взаимное торможение электрич. и магнитного полей при всяких их изменениях. Если например напряженность поля Е (фигура 8) растет по абсолютной величине, то возникает магнитное поле Н (правый винт), которое, усиливаясь с ростом Е, возбуждает в свою очередь электрич. поле E (левый винт), которое направлено противоположно Е, и т. о. ослабляет рост Е. Обратно, при убывании Е поле Е будет поддерживать Е, замедлять это убывание. Если бы различия в знаке в ур-иях (24) и (20а) не было, то индуцированное возрастанием Е поле E было бы направлено по Е, что влекло бы за собой все большее, ничем не ограниченное возрастание напряженности поля. Аналогичное торможение имеет место и при всех изменениях токов проводимости. Им обусловливается постепенность нарастания силы, уменьшение амплитуды силы переменного тока при увеличении самоиндукции цепи тока и т. д.

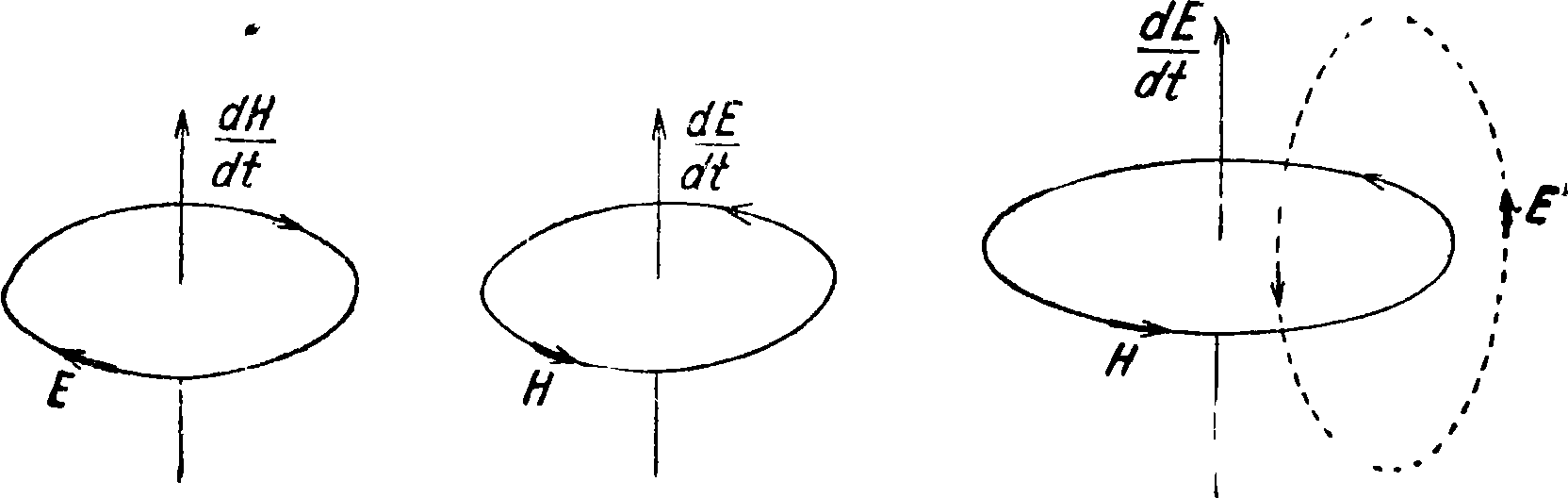
Фигура 7. Фигура 8.

Заметим в заключение, что с точки зрения современных теоретич. представлений единственной общей характеристикой тока проводимости и электрич. тока смещения (25) является возбуждение обоими токами магнитного поля по одинаковому закону. Во всех же прочих отношениях токи проводимости и токи смещения не имеют между собой ничего общего. Токи проводимости обусловливаются движением электрич. зарядов, токи же смещения вовсе не связаны с каким-либо перемещением зарядов или даже с наличием их в данном участке пространства — они имеют место и в вакууме и характеризуют лишь изменение во времени напряженности электрич. поля. Поэтому токи смещения отличны от нуля только в переменном поле, тогда как токи проводимости могут существовать и в поле постоянном. Наконец токи проводимости связаны с нагреванием проводников, тогда как токи смещения никакого выделения тепла не обусловливают.

Некоторые следствия Максвел .новых уравнений поля. Ур-ия (20а) и (24) являются основными уравнениями электромагнитного поля. Может показаться странным, что при выводе этих ур-ий основной закон электростатики — закон Кулона — повидимому нигде явно учтен не был. Однако этот закон непосредственно связан с некоторыми следствиями, вытекающими из формул (20а) и (24). Дело в том, что эти ур-ия связывают циркуляцию электрич. и магнитного векторов £ и Я по произ-

вольному замкнутому контуру L с магнитным потоком или с полным электрич. током, протекающим через ограниченную этим контуром поверхность S. При этом вовсе не указывается, о какой из бесчисленного множества различных, вообще говоря, искривленных поверхностей S, ограниченных этим контуром, идет в данном случае речь. Стало быть, если эти ур-ия вообще имеют какой-либо смысл, то через любые две поверхности S_x и S₂,ограниченные одним и тем же контуром Z/, всегдадолжен протекать одинаковый магнитный поток и одинаковый полный электрич. ток. Таково необходимое следствие из ур-ий (20а) и (24), полностью подтверждаемое опытом.

Фигура 9. Чтобы выразить это следствие в ма-

тематич. форме, рассмотрим две произвольные поверхности Si и S2, ограниченные одним и тем же контуром L и стало быть образующие в совокупности одну замкнутую поверхность (фигура 9). Применяя например ур-ие (20а) к поверхностям Si и S₂, получаем:

Φ^ε*<»=-τ!ϊ ^H«i^ds=-TiJ ^н^’

L Si S₂

где п и «2 по условию — нормали к Si и S₂, выбранные так, чтобы их направления образовали с направлением обхода контура L правовинтовую систему (фигура 9). Из последнего ур-ия следует:

S₂

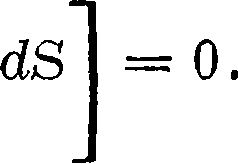
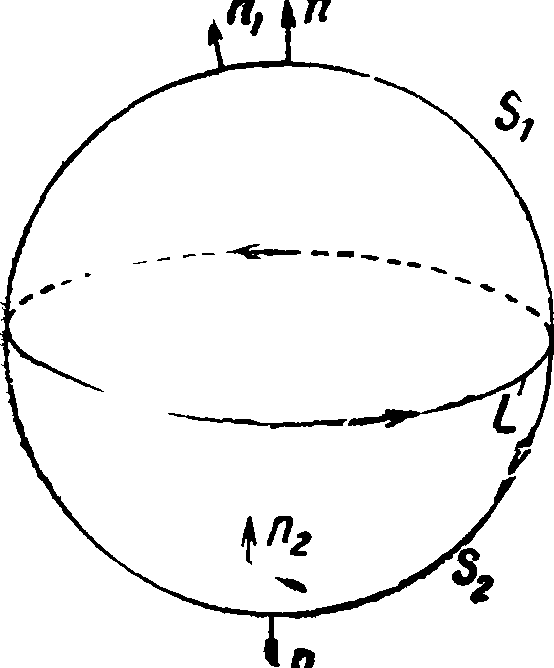
Если мы теперь через п обозначим внешнюю нормаль из замкнутой поверхности S (то есть нормаль, направленную от внутренней ее стороны к внешней), то п на участке Si совпадает с п, а на участке S₂ будет прямо противоположна «2- Стало быть

Κ„ι=Η_η и Н_п2=— Н_п, и т. о. последнее ур-ие принимает вид

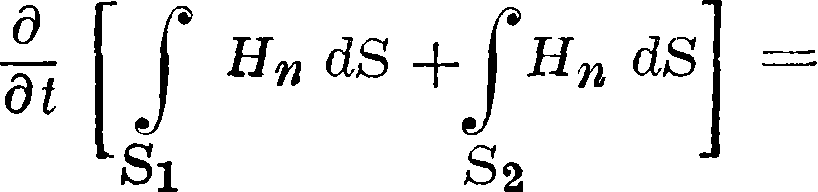
= ~ ф Н_я <JS=0. (26)

S=Si + ^s2

Это ур-ие должно очевидно удовлетворяться для любой замкнутой поверхности S, ибо на всякой замкнутой поверхности можно провести замкнутый контур L, разбивающий ее на две ограниченные этим контуром части Si и S2. Аналогичным образом из ур-ия (24) получаем для произвольной замкнутой поверхности S:

4я(£ )_м dS + ~ ф Е„ dS=0. (27)

S S

Комбинируя это ур-ие с ур-ием непрерывности (8а), получаем

££B_ndB-t*£f_edV-0.

S V

или

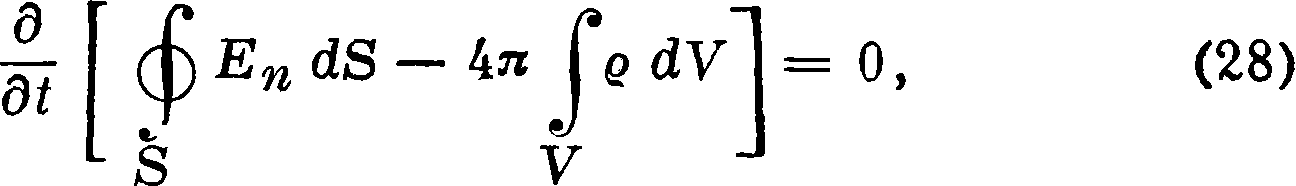
где У — объём, ограниченный поверхностью S.

Из (26) следует, что значение взятого по произвольной замкнутой поверхности интеграла

(j) Н_п dS постоянно во времени и ни при каких физических процессах изменяться не может. Приняв во внимание, что в отсутствии магнитного поля этот интеграл очевидно равен нулю, заключаем, что равенство

§н_п

S

dS=0

осуществляется всегда и для всякой замкнутой поверхности S. Аналогичным образом из равенства (28) следует, что

(j) Е_п dS=ίπ j* ρ dV. (30)

S У

Ур-ие (30), выражающее т. н. теорему Гаусса, в случае электростатич. поля м. б. легко выведено из закона Кулона.

Действительно, пусть поверхность S представляет собой сферу радиуса R, в центре которой находится точечный заряд q. Поле Е этого заряда направлено радиально,

так что на поверхности сферы Е_п — ± Е — и следовательно ^к

(jj Е„ dS= ^ (j) Sd=· 4*й“=4яд,

S S

что при любом радиусе сферы R совпадает с ур-ием (30). Исходя из закона Кулона, можно далее показать, что это ур-ие применимо не только к сфере, но и к любой замкнутой поверхности, охватывающей заряд q. Наконец при объёмном распределении зарядов электрич. поле Е складывается из полей отдельных элементов заряда dq — ρ dV, каждое из которых удовлетворяет последнему ур-ию. Основываясь на этом, можно доказать справедливость ур-ия (30) для произвольного Ку-лонова поля.

То обстоятельство, что правая часть ур-ия (29) в отличие от ур-ия (30) равна нулю, выражает собой тот факт, что в отличие от зарядов электрических никаких магнитных зарядов не существует. Пользуясь представлением об электрич. и магнитных силовых линиях, можно, как известно, выразить содержание ур-ий (29) и (30) след, обр.: электрич. силовые линии начинаются на отрицательных и оканчиваются на положительных зарядах (направление силовых линий является конечно условным; при принятом выше условии о направлении вектора Е нужно считать, что силовые линии исходят из положительных зарядов и оканчиваются на отрицательных), тогда как магнитные линии всегда замкнуты либо во всяком случае не имеют ни начала ни конца.

Система у p-и и электромагнитного поля. Система уравнений (20а) и (24),· ур-ия непрерывности (8а) и закона Ома (48), а также непосредственно связанных с этими четырьмя ур-иями уравнений (29) и (30) охватывает собой всю совокупность (макроскопических) электромагнитных явлений в отсутствии диэлектриков и магнетиков (при условии неподвижности проводников). При указанных ограничениях макроскопич. теория Э. сводится в сущности к исследованию этих законов электромагнетизма и к нахождению следствий, вытекающих из них для различных частных областей электромагнитных явлений (электростатика, постоянные и переменные токи, электромагнитные волны и тому подобное.). Все частные закономерности этих явлений, как например закон Кулона (1), закон Био-Савара (13) и т. д., являются простыми следствиями этих ур-ий поля. Мы приведем здесь еще раз систему уравнений (20а), (24), (29), (30) и (18), носящих название у p-и и Максвелла:

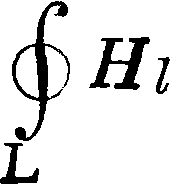
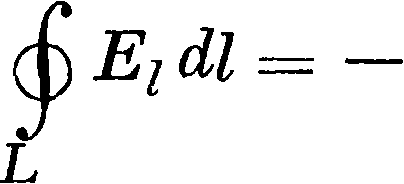
1 JL

с dt

Н_п dS,

S

^dl=‘ + TT,S^Et‘^{dS +} Tfin^dS>

S S

j)E_ndS=4π J qdV,

(I)

(II)

(29)

(III)

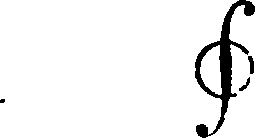
s

H_ndS=0,

i=y£,

а также ур-ие непрерывности

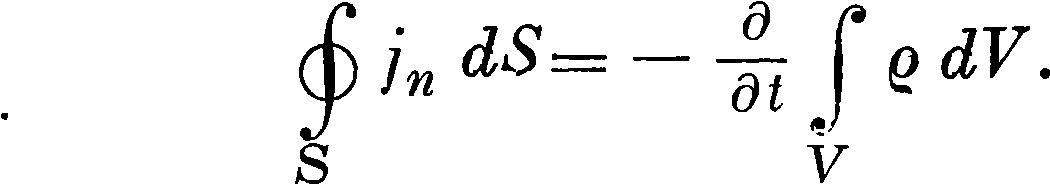
(IV)

(V)

(VI)

С помощью этих обозначений диференциальные ур-ия, эквивалентные интегральным ур-иям (I)—(IV) и (VI), записываются след. обр.

1 dH
rot E —-дт, с dt	(Г)
dF Lit.
rot Η=— — + - j, c dl. с	(И>
div E=4πρ,	(ΠΓ>
div Η=0,	(IV)

[В предыдущем мы, исходя из (I), (II) и (VI), путем некоторых добавочных рассуждений получили (III) и (IV). Обратно, из ур-ий (I)—(IV) непосредственно вытекает справедливость ур-ия непрерывности (VI)].

В том случае, если в проводниках действует помимо Е также и сторонние эдс, которые можно охарактеризовать соответствующей напряженностью поля этих сил Е_стр, ур-ие (V) нужно дополнить след, обр.:

j=_V(E+E_cmp.). (V)

Заметим, что основные ур-ия электронной теории в общем совпадают с приведенными ур-иями Максвелла. Отличие заключается лишь в трех пунктах. Во-первых, в электронной теории плотность тока выражается непосредственно через плотность и скорость зарядов (9а)

j=QO, (Va)

во-вторых, зависимость плотности тока от поля выражается не феноменологическим ур-ием (V) и (V), а определяется из (Va) и из ур-ий движения электронов и протонов, основывающихся на лоренцовом выражении силы (5):

£ (то)=/>=*{£ +Ь [вЯ]J, (V6)

где т — масса заряда q. Наконец в электронной теории система уравнений (I)—(IV), (Va),

(V6) и (VI) предполагается справедливой всегда при всех условиях, и особенности электромагнитных явлений в различных весовых телах — проводники, диэлектрики и т. д. — объясняются на основе рассмотрения сложной электронной структуры этих тел.

Диференциальная форма уравнений поля. Уравнения поля (I)—(VI) носят характер интегральных соотношений и связывают например значения вектора Н на произвольном контуре L со значениями вектора j во всех, вообще говоря, удаленных от этого контура точках поверхности S. Однако лишь ф о-р м а этих ур-ий может представляться соответствующей представлениям теории дальнодействия. Простые математические преобразования позволяют выразить уравнения поля в диферен-циальной форме, в которой непосредственно обнаруживается соответствие этих уравнений законам близкодействия.

Для записи этих диференциальных уравнений удобно воспользоваться обозначениями векторного исчисления (смотрите) и введенными там понятиями о дивергенции и вихре, или роторе (смотрите), данного вектора. Если А есть вектор, слагающие которого А_х, Ay, A_z являются непрерывными ф-лами координат, то дивергенцией век-то р а А называется скаляр, обозначаемый через div А и равный

,. * дА_Т, дА_г,

div А=-г-* Н--«

dx dy

dA_z

dz

(31)

Далее, ротором, или вихрем, вектора А называется вектор, обозначаемый через rot Л (или curl Л), слагающие которого соответственно равны

rotr Л=

dAz

by

д_Ау

dz

rot“, Л =

rot₂ А=

д_А_у

dx

дА_х

dy

0_Αχ

dz

dA_zdx ’

div у=—

do

dt

(VI)

Отметим еще раз, что уравнения (I)—(IV) и (VI) полностью эквивалентны ур-иям (I) — (IV) и (VI); из каждого интегрального уравнения однозначно вытекает справедливость соответствующего диференциального ур-ия и обратно.

Из этих ур-ий непосредственно явствует, что законы электродинамики носят характер законов близкодействия. Поля Е и Н в данной точке пространства Р и в данный момент времени t однозначно определяются полностью движением зарядов и напряженностью поля, относящимися к смежным с Р точкам пространства ик смежным с t моментам времени, вне всякой непосредственной зависимости от состояния зарядов и поля в удаленных участках пространства или в предшествовавшие t отрезки времени. Ибо, с одной стороны, ур-ия (I)—(IV) устанавливают о д-нозначную связь между значениями, которыми обладают величины ρ и и производные от Е и Н по координатам и по времени в данной точке Р в данный момент г, а с другой стороны, самые значения производных от Е и Н однозначно определяются значениями Е и Н в бесконечно близких к Р точках в бесконечно близкие к t моменты времени.

Скорость распространения поля и запаздывающие потенций-л ы. Уравнения поля, обладая характером законов близкодействия, вместе с тем м. б. рассмотрены и с несколько иной точки зрения. В предыдущем неоднократно подчеркивалось, что элек-трнч. поле может возбуждаться не только непосредственно зарядами, но и изменениями поля магнитного и обратно. Однако в конечном счете источниками электромагнитного поля являются только заряды и их движение (токи проводимости, а не токи смещения). Другими словами, уравнения (I)—(IV) можно преобразовать так, чтобы поле в любой точке пространства определялось только распределением и движением зарядов. Однако при этом сказывается то обстоятельство, что действие зарядов и токов распространяется не мгновенно, а с конечной скоростью с. Поэтому поле в данной точке Р в момент t определяется не мгновенным распределением и движением зарядов в тот, же момент t и в той же точке Р, а распределением и движением зарядов во всем пространстве в предшествующие t моменты времени.

Результат такого преобразования выражается наиболее просто, если ввести в рассмотрение две вспомогательные величины—т. наз. скалярный и векторный запаздывающие потенциалы электромагнитного поля φ и h, С помощью этих величин напряженности поля Еж Н выражаются следующим образом:

Е — — grad ψ —

1

с д_А

dt

(33)

Н=rot А

(32)

где grad φ — градиент (смотрите) скаляра φ. С другой стороны, φ и А выражаются через плотность зарядов и“ токов ρ и j следующим образом:

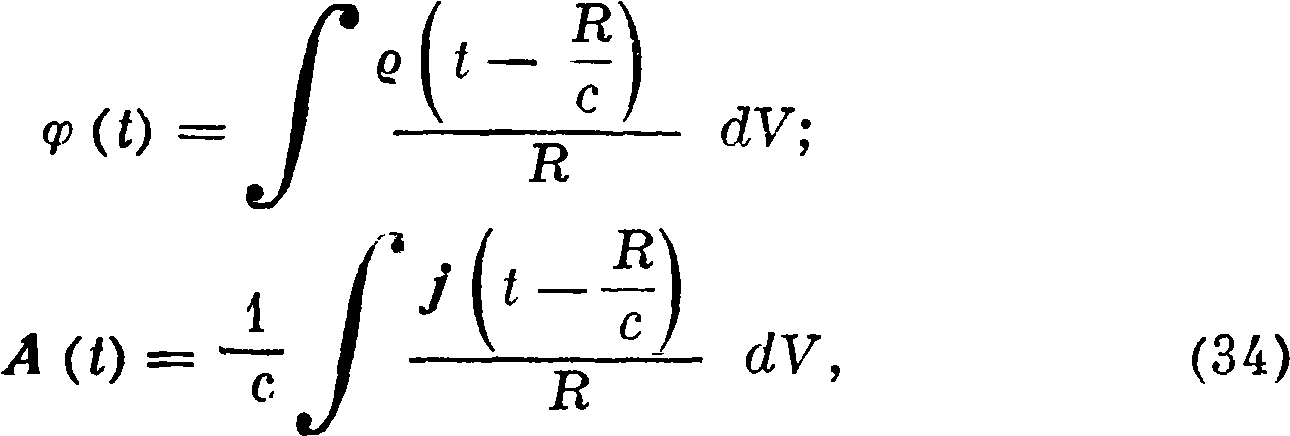
где объёмные интегралы должен быть распространены по всему бесконечному пространству. Смысл этих выражений таков. Чтобы определить например значение ψ в точке Р в момент t, нужно для каждого элемента пространства dV вычислить произведение

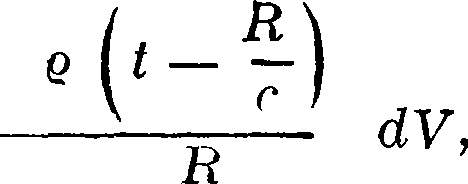
где R — расстояние этого элемента от рассматриваемой точки поля Р, а ρ — ^ —значение плотности Э.,

имевшейся в этой точке в предшествующий t момент t — —. Сумма произведений этого вида по всему •объёму и даст искомое значение φ. Т. о. действие зарядов и токов, удаленных от Р на расстояние R, сказывается в Р лишь по прошествии промежутка времени R/c. Это значит, что электромагнитные действия зарядов и токов распространяются не мгновенно, а со скоростью с равной скорости света.

Эквивалентные системе (I) — (V) ур-ия (33) и (34) показывают, во-первых, что источником поля в конечном счете являются только заряды и их движение и, во-вторых, что все электромагнитные действия распространяются с одинаковой конечной скоростью с.

Весьма существенно, что значение этой постоянной с м. б. определено двумя совершенно независимыми методами. Во-первых, с входит в уравнения (11) и (13), определяющие магнитное поле токов и силы, действующие со стороны данного магнитного поля на находящиеся в нем токи. Т. о. значение т. н. электродинамической постоянной см. б. определено например путем измерения механич. или пондеромоторных сил взаимодействия постоянных токов. С другой стороны, значение с м. б. определено путем непосредственного измерения скорости распространения электромагнитных возмущений, например электромагнитных (в частности световых) волн. Совпадение результатов измерения с этими совершенно различными Методами является одним из наиболее убедительных подтверждений всей современной теории Э. Пользование наряду с уравнениями (I)—(IV) также и уравнениями (33) и (34) характерно для современной теории. Э. Фарадей-Максвелла теория сосредоточивала все внимание на поле, не приписывая зарядам никакой самостоятельной значимости. С точки зрения этой теории термин «заряд» являлся в сущности лишь кратким обозначением тех участков поля, в которых сумма

ЗЕ д F

производных напряженности поля +

OF “

+ -q^= diY Е оказалась отличной от нуля [см. уравнение (III)]. Электронная же теория восстановила заряд в его правах источника поля. Заметим в заключение, что электромагнитные потенциалы φ и А играют существенную роль также и в теории постоянного электромагнитного поля. В этом случае как ρ и j, так и φ и А от времени не зависят, и вычисление интегралов (34) значительно упрощается. Далее, в виду независимости А от времени, электрич. поле согласно (33) однозначно определяется одним только скалярным потенциалом φ, а магнитное — только векторным потенциалом А. Т. о. электрическое и магнитное поле в этом случае оказываются независимыми друг от друга. Заметим, что в случае постоянного электрич. поля потенциал φ, определяемый ур-ием (34), совпадает с потенциалом φ, определяемым из работы сил электрич. поля [ур-ие (16)].

Энергия электромагнитного поля. Поток энергии. Как уже указывалось выше, электромагнитные явления нами, вообще говоря, непосредственно не воспринимаются, так что судить о них мы можем только по сопровождающим их переходам энергии (механической, тепловой, химической и т. д.). Поэтому система ур-ий поля приобретает физич. смысл лишь в том случае, если к ней присоединить выражение энергии электромагнитного поля. В теории Максвелла, базирующейся на ур-иях (I)—(V⁷), выражение энергии поля не м. б. выведено из этих ур-ий и должен быть постулировано независимо от этих ур-ий на основе обобщения данных опыта. Напротив, исходя из ур-ий электронной теории, отличающихся (в рамках рассматриваемой в этой главе области явлений) от ур-ий Максвелла лишь заменой ур-ия (I) или (I⁷) на ур-ия (Va) и (V6), можно однозначно вывести выражение электромагнитной энергии без-каких-либо добавочных допущений. Ибо, с одной стороны, ур-ие (V6) определяет силы, действующие на электрические заряды, а с другой стороны, с точки зрения электронной теории первым этапом перехода энергии поля в другие формы всегда является переход ее в механич. кинетич. энергию движения элементарных электрич. зарядов, которая затем может уже в свою очередь переходить в энергию тепловую, химическую и т. д. Существенно, что энергия электромагнитного поля выражается одинаковым образом и в теории Максвелла и в электронной теории (в случае отсутствия диэлектриков и магнетиков).

Вывод этого выражения из ур-ий электронной теории таков.

Сила, действующая на точный заряд q, выражается ф-лой Лоренца (δ). Если же исходить из объёмного распределения зарядов с плотностью о, то сила, действующая на находящийся в элементе объёма dV элемент заряда dq=q dV, выразится очевидно аналогичной ф-лой:

dV=ρ j E + -i- νΗ] J dV.

Работа, совершаемая этой силой за единицу времени, будет равна произведению ее на путь, проходимый зарядом в 1 ск., то есть на v:

vf dV — ovEdV.

В выражение работы входит только Е, ибо силы магнитного поля [vH] перпендикулярны перемещению заряда V и поэтому никакой работы не совершают. Наконец полная работа А, совершаемая силами Электромагнитного поля в некотором объёме dV за единицу времени, равна сумме (или интегралу) работ, совершаемых в каждом его элементе dV:

_L=J qvEdV=JjE

dV

(35)

(смотрите ур-ие Va). Пользуясь ур-ием поля (Г)—(IP), можно“ выразить плотность тока J через напряженности поля и затем привести (35) к след, виду:

dV -

4 π

) [ЕН]_п dS, (36)

где S—замкнутая поверхность, ограничивающая объём V. Из (IF) следует:

с. „ 1 дЕ

^J 4π^{Γθί Н} kndt

В векторном анализе доказывается, что для любых двух векторов Е и Н справедливо равенство

Е · rot Н=Н · rot E — div [ЕМ].

Стало быть

je= -к«*я_Е-

Т- div [ЕН] —

4 π

дЕ

dt *

Внося сюда значение rot Е из {V), получаем

^dJi

dt

Ϊ д

#--Ы^{н + в}ъ)-ъ^л*^1ЕН]-

— 8=ет ^{(Е2 + Я2)}-

4 π

div [ЕН].

Внося это в (35) и приняв наконец во внимание, что согласно теореме Гаусса

I div [EH] dV=(j)[EH]_ndS,

V s

получаем (36). Если внести обозначения

W=-i J [Е2 _|_ НЦ dV (37)

V

то ур-ие (36) примет «ид:

dW

dt

- (t) р„ ds.

(38)

(39)

Предположим сначала, что объём интегрирования V обнимает собой все электромагнитное поле (то есть вообще говоря, все бесконечное пространство) и что последний член ур-ия (39), представляющий собою интеграл по (вообще говоря, бесконечно удаленной) поверхности S, охватывающей это поле, равен нулю. Тогда ур-ие это примет вид:

₄ dW

^{А =} - ж-

Стало быть, работа сил электромагнитного поля за единицу времени равна убыли ф-ии W за то же время. А это и значит, что эта ф-ия W выражает собой энергию электромагнитного поля, за счет которой производится работа сил этого поля.

В том случае, когда мы рассматриваем нек-рый конечный объём У, не охватывающий собой всего поля, убыль находящейся в этом объёме энергии

W=~ J (E* + Н2) dV

V

может обусловливаться не только затратой части этой энергии на работу А, но и выходом другой ее части, сохраняющей форму энергии электромагнитной, за пределы объёма У. Иными словами, энергия поля может вытекать через-граничную поверхность S за пределы объёма У. Так например, электромагнитная волна, излучаемая каким-либо находящимся внутри У источником и распространяющаяся за пределы поверхности S, уносит с собой соответствующее количество поверхности электромагнитной энергии. Переписав ур-ие (39) в форме

-%-А+фъ“,

S

мы убеждаемся, что убыль энергии — действительно складывается из работы А, совершаемой внутри объёма У, и из утечки энергии (j) Р_п dS через границу этого S

объёма У. (Конечно величина этой утечки м. б. и отрицательной, если вектор Р направлен внутрь поверхности S, то есть проекция его Р_п на внешнюю нормаль к поверхности отрицательна; в этом случае энергия втекает извне внутрь объёма У.) По существу же величина этой утечки зависит только от напряженностей поля Е и Н на границе объёма У [ибо только ими согласно (38) и определяется значение Р на этой границе].

Т. о. поток электромагнитной энергии, протекающий за единицу времени через замкнутую поверхность S, равен <§)P„dS, причем вектор

S

Р определяется уравнением (38). Это положение называется теоремой Пойнтинга, а вектор Р — вектором Пойнтинга. Теорема Пойнтинга играет важнейшую роль при изучении всех процессов излучения электромагнитных волн.

Часто из теоремы Пойнтинга делается тот вывод, что в каждой точке поля поток энергии равен Р, то есть что через проходящую через данную точку поля площад ку в 1 см%, перпендикулярную вектору JP, протекает за единицу времени в направлении этого вектора Р единиц энергии. Применение этого положения к произвольной замкнутой поверхности действительно приводит нас вновь к доказанному только что ур-ию (39). Однако положение это, позволяющее дать весьма простое и наглядное истолкование ряду явлений, выходит за пределы теоремы Пойнтинга, доказанной для замкнутых поверхностей, и не м. б. строго обосновано. Ибо в каждой отдельной точке поля поток энергии может отличаться от Р на нек-рую величину Т, причем теорема Пойнтинга не будет нарушена, если только линии потока Т замкнуты и если таким образом поток Т выносит из произвольного объёма У столько же энергии, сколько и вносит в него.

Весьма существенно, что выражение энергии (37) и теорема Пойнтинга (39) дают возможность локализовать в пространстве энергию электромагнитного поля, то есть возможность указать, какое количество энергии находится в любом заданном объёме F. Этим теория поля существенно отличается от теории дальнодействия. Согласно последней например энергия взаимодействия двух зарядов д_г и д₂, находящихся на расстоянии R друг от друга, равна

W=^qiQ2

(40)

и не м. б. однозначно локализована в определенных участках пространства, ибо она определяется относительным положением этих удаленных друг от друга зарядов. Конечно ч и-елейное значение электрич. энергии взаимодействия правильно выражается формулой (40), правда, лишь при условии неподвижности зарядов д_г и ρ₂, и самая формула эта м. б. получена путем преобразования ф-лы (37). Действительно, пусть Е_г и Е₂ — напряженности поля заряда д_ги поля заряда д₂, так что напряженность результирующего поля обоих зарядов равна Е== Е_г + Е₂. Тогда полная электрич. энергия будет согласно (37) равна

= L Я? dV + I j Е_ХЕ, dV+ L· j El dV.

Первый и последний члены этой суммы выражают т. наз. собственную энергию зарядов д_г и д₂, не зависящую от их взаимодействия. Так например,

-g¹— J E dV равно той работе, которую соверши ли бы силы взаимного отталкивания отдельных элементов заряда q_lt если бы эти элементы разлетелись в разные стороны и удалились в бесконечность. Понятно, что собственная энергия любого заряда всегда положительна. Член же

PF_i2 — 4π J* E_xE₂dV (41)

очевидно существенно зависит от взаимного расположения зарядов д_х и д₂ и выражает энергию их взаимодействия.

Пользуясь ур-иями поля, можно строго показать, что в случае «точечных» неподвижных зарядов выражение W₁₂ сводится к (40). В частности при бесконечном удалении зарядов (R== оо) W₁₂, как и выражение (40), обращается в нуль, ибо в этом случае там, где поле Е_х заряда д_х отлично от нуля, поле Е₂ бесконечно удаленного заряда д₂ равно нулю и обратно.

II. Электромагнитное поле в диэлектриках и магнетиках. С точки зрения электронной теории уравнения поля (I⁷)—(IV⁷) применимы ко всем электромагнитным явлениям. Однако при обыкновенном макроскопическом рассмотрении явлений нас интересуют не точные микроскопии, значения основных электромагнитных величин ρ, у,

Е и //, существенно меняющиеся в весомых телах от атома к атому и даже в пределах одного и того же атома, а лишь средние макроскопич. значения этих величин. Макроскопическим значением какой-либо величины называется среднее ее значение в произвольном и физически бесконечно малом объёме. Так называются, в отличие от математических бесконечно малых, такие элементы объёма, которые еще очень велики по сравнению с расстояниями между молекулами среды, а стало быть и по сравнению с микроскопич. неоднородностями среды и поля, но вместе с тем уже чрезвычайно малы по сравнению с макроскопич. неоднородностями. Другими словами, средние значения физич. величин (ρ, j, Е, Н и т. д.) в любом из этих элементов должны бесконечно мало отличаться от средних значений тех же величин в смежных с ним элементах объёма, в пределах же каждого элемента атомистич. структура среды должна полностью сглаживаться. Т. о. одна из задач теории состоит в нахождении уравнений макроскопич. поля путем усреднения точных ур-ий поля (Г)—(IV). Наиболее трудной частью этой задачи является нахождение среднего для данной среды значения плотности Э. ρ и плотности тока j. При этом необходимо проводить различие, с одной стороны, между зарядами свободными и зарядами связанными, с другой стороны, между токами проводимости и токами молекулярными.

Свободными зарядами называются заряды, могущие под воздействием электрич. поля перемещаться в пределах данной среды по направлению действующих на них сил. Таковы т. наз. свободные электроны в мет, ионы в растворах электролитов и т. д. Все же остальные заряды, входящие в состав нейтральных атомов или молекул или же в состав ионов, неподвижно закрепленных в определенных местах кристаллической решетки твердого тела, называются зарядами связанными. Эти определения отличаются от широко распространенной, но с современной точки зрения нерациональной терминологий, согласно которой наши свободные заряды носят название истинных (wahre), а свободными зарядами называется совокупность истинных и связанных зарядов. В отсутствии электрич. поля наличие связанных зарядов в данном веществе ни в чем непосредственно не проявляется (при макроскопическом его изучении), ибо действия зарядов противоположных знаков, находящихся в каждом элементе объёма тела в равном числе, взаимно компенсируются. При возникновении же электрич. поля связанные заряды, хотя они и не могут перемещаться на расстояния макроскопич. порядка величины, смещаются в пределах каждого атома или молекулы тела по направлению действующих на них сил, причем заряды противоположных знаков смещаются в противоположные стороны. Это смещение связанных зарядов носит название поляризации д и электр и-к а. Благодаря этой поляризации средняя плотность связанных зарядов внутри диэлектрика может стать отличной от нуля, что в свою очередь естественно отражается на напряженности элек-^г)рич. поля.

На первый взгляд может показаться, что если каждая молекула диэлектрика нейтральна, то есть содержит в себе одинаковое количество зарядов противоположных знаков, то и средняя плотность связанных зарядов в диэлектрике должна равняться нулю. Выделим однако в ди

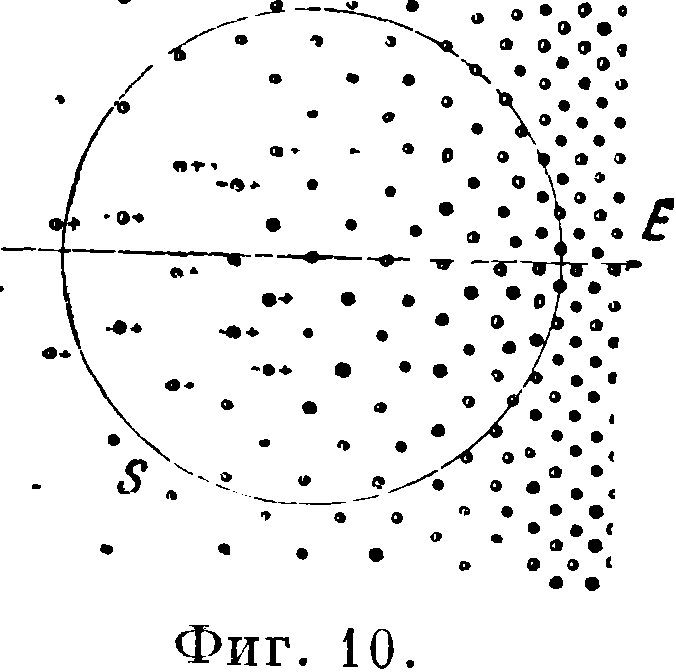
электрике поверхностью S некоторый конечный объём V, размеры которого велики по сравнению с расстояниями между молекулами (фигура 10). Вообще говоря, поверхность пересечет нек-рое число молекул так, что одни из зарядов этих молекул окажутся вне объёма F, а другие внутри его. Поэтому, несмотря на то, что каждая молекула диэлектрика в целом нейтральна, общий заряд объёма F, а стало быть и средняя плотность электричества в нем могут оказаться отличными от нуля. Если распределение зарядов во всех молекулах одинаково, то в среднем число отсеченных поверхностью S положительных зарядов молекул будет равно числу отсеченных ей отрицательных зарядов, и общий заряд внутри S будет в среднем равен нулю. Пусть однако в объёме существует внешнее электрич. поле, направленное например слева направо. Тогда положительные заряды молекул будут смещены вправо по отношению к отрицательным, так что левая часть поверхности S будет отсекать положительные заряды молекул, а правая ее часть — заряды отрицательные. Если к тому же смещение зарядов молекул справа больше, чем слева, например в виду возрастания электрич. поля, или если плотность молекул возрастает слева направо (этому случаю соответствует фигура 10), то число отрицательных зарядов в объёме V будет превышать число зарядов положительных и общий заряд этого объёма окажется отличным от нуля. Т. обр. при наличии внешнего электрич. ofy поля средняя плотность связанных зарядов отлична от нуля, если только это поле Фигура И. неоднородно (то есть различно в различных участках пространства) или если сам диэлектрик неоднороден.

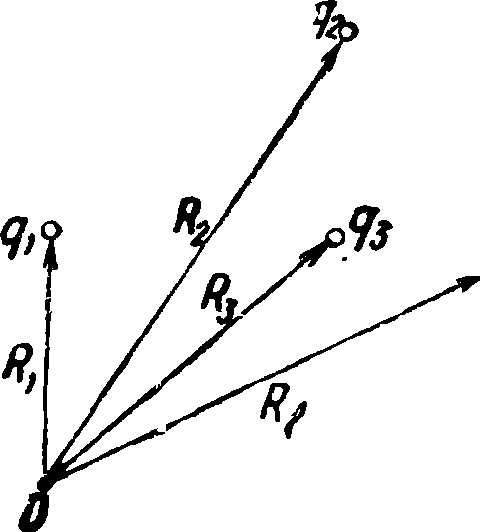
Чтобы количественно определить плотность связанных зарядов, нужно, предварительно познакомиться с количественной характеристикой электрического состояния нейтральной молекулы и нейтрального тела вообще. Такой характеристикой относительного распределения зарядов нейтральной молекулы служит ее электрический момент. Если д_г, д₂, д₃. — элементарные заряды (электроны и положи- О* тельные ядра атомов), входящие в состав молекулы, а /?_1} /?₂, /?₃. — расстояния этих зарядов от произвольной начальной точки отсчета О (фигура 11), то электрич. моментом р молекулы называется векторная сумма р=2 ь ^Ri- <⁴²)

Фигура 12.

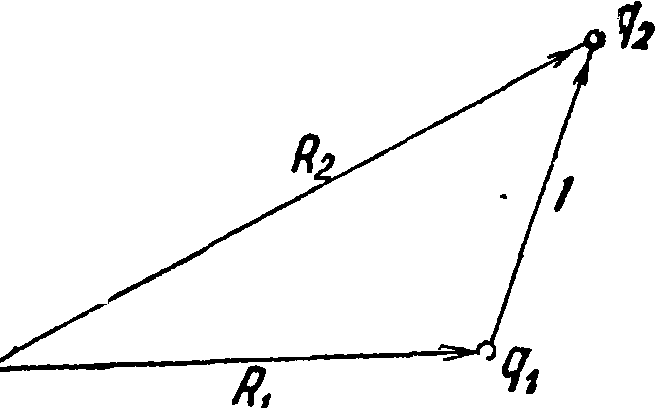
Значение этого вектора р, как можно показать, не зависит от выбора точки О; если молекула нейтральна, то есть если Σ^·=0. В частном случае, если молекула сводится к совокупности двух равных зарядов д_г и д₂ противоположных знаков: д₂=—д_г =-. д>0 (т. наз. электрический диполь), то момент ее равен (фигура 12)

Р — ⁽1 Р Я2Р2 — Я (Pi — ^2) — (42а)

то есть представляет собой вектор, направленный от отрицательного заряда молекулы к положительному. Вообще, если положительные и отрицательные заряды симметрично расположены около центра молекулы, то р — 0; если же положительные заряды в среднем смещены по отношению к отрицательным по какому-либо определенному направлению, то вектор р будет направлен по этому направлению, а его численная величина будет являться мерой этого смещения. Поляризацией единицы объёма диэлектрика Р называется векторная сумма электрич. моментов всех молекул, находящихся в единице его объёма: ^N

ρ=Σρ> <⁴³>

или, точнее, сумма моментов молекул, находящихся в элементе объёма dV, деленная на величину этого элемента

Р=%. (43а)

При отсутствии внешнего электрич. поля поляризация диэлектрика Р=0; вообще же говоря, она пропорциональна средней макроскопич. напряженности поля Е:

Р=аЕ, (44)

где «коэф. поляризуемости» а зависит от природы диэлектрика. Охарактеризованная выше зависимость средней плотности связанных зарядов Ясвязн. ^от неоднородности поля и среды находит себе количественное выражение в след, ф-ле:

W=-(^ + ^f + f-*)=-divP. (45)

Чертой сверху здесь и в дальнейшем мы обозначаем средние макроскопич. значения данной величины. Обозначая далее через о_микр0 и д_свбд#истинные микроскопии, значения полной плотности зарядов и плотности зарядов свободных, мы т. о. получаем:

Ямикро Ясвбд. “b Ясвязн. ~ Ясвбд. 7^. (46)

Прежде чем перейти к вопросу о средней плотности токов, сделаем несколько предварительных замечаний. Магнитные свойства всякого элементарного замкнутого тока, то есть поле этого тока и силы, действующие на него во внешнем поле, полностью характеризуются т. н. магнитным моментом М этого тока. При этом ток называется элементарным, если выполнены два условия: 1) внешнее магнитное поле не меняется сколько-нибудь заметно в занимаемом током участке пространства и 2) возбуждаемое током поле рассматривается лишь в удаленных от него точках пространства, расстояние которых от тока значительно превышает его размеры. Вектор магнитного момента для линейного замкнутого тока силы 1 равен

M=±is, (47)

где S — величина площадки, охватываемой током (для простоты предполагаем, что площадка эта плоская), причем вектор М направлен перпендикулярно к площадке S и образует с направлением тока правовинтовую систему. Если бы существовали магнитные заряды т, подобные зарядам электрическим и взаимодействующие между собой по закону Кулона F=m₁ m₂/R² (1), то по аналогии с диполем электрическим можно было бы говорить о диполе магнитном, состоящем из двух равных и противоположных по знаку магнитных зарядов т₁ и т₂ гп₂=— m =

= т > 0. Магнитный момент М такого диполя по аналогии с (42а) выразился бы ф-лой

М — ml, (48)

где I — вектор, проведенный из отрицательного заряда диполя к положительному. Можно показать, что элементарный ток момента М и в активном и в пассивном отношении (то есть и в отношении, возбуждаемого им поля и в отношении действующих на него сил) совершенно эквивалентен магнитному диполю того же момента М. Этим именно и объясняется тот факт, что в 19 в основные известные тогда магнитные свойства весомых тел могли успешно объясняться на основе предположения о существовании в молекулах этих тел магнитных зарядов и магнитных диполей. Хотя мы знаем теперь, чта магнитные свойства молекул объясняются движением электрич. зарядов в них, однако совре“ менная терминология магнетизма носит на себе еще отпечаток этой теории магнитных диполей. Заметим далее, что намагничением единицы объёма какого-нибудь тела называется векторная сумма магнитных моментов всех молекул (то есть магнитных моментов всех молекулярных токов), находящихся в единице его объёма,

/=2^Ж <⁴⁹> или, точнее, сумма моментов молекул, находящихся в элементе объёма dV, деленная на величину этого элемента dV

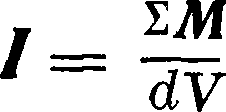
[сравни (43) и (43а)]. Очевидно, что намагничение м. б. также названо магнитной поляризацией.

Переходя к вопросу о средней плотности токов в весомых телах, заметим, что токами проводимости в узком смысле слова (в широком смысле слова токи проводимости, или конвекционные, противопоставляются токам смещения и включают в себя токи молекулярные) называются обычные токи, обусловленные движением в проводниках свободных зарядов (свободных электронов, ионов и тому подобное.), тогда как токами молекулярными называются токи, обусловленные движением связанных зарядов в пределах каждой отдельной молекулы. Так как молекулярные токи всегда замкнуты в пределах отдельной молекулы, то средняя плотность их в каждой молекуле равна нулю:

J7», dV= 0,

У

где V — объём молекулы. Это однако не препятствует тому, что средняя плотность молекулярных токов в пределах произвольного физически бесконечно малого объёма.V м. б. отличной от нуля, ибо пограничная поверхность S этого объёма может рассекать на части ряд отдельных молекул. Рассуждения, совершенно аналогичные рассуждениям, приведенным выше для случая диэлектриков, приводят к следующему результату. Средняя макроскопич. плотность молекулярных токов след. обр. связана с намагничением среды/:

= crot (50)

[см. ур-ие (32)]. Впрочем в этом выражении учтены лишь замкнутые постоянные молекулярные токи, от распределения которых только и. зависит намагничение /. Между тем перемен-

ное электрич. поле вызывает изменение поляризации тела Р, то есть соответствующие смещения связанных зарядов молекул; иными словами, оно возбуждает дополнительно к рассмотренным еще и переменные незамкнутые молекулярные токи. Средняя плотность их, как легко убе-цр диться, равна Из (43а) и (42) следует

Ι^ράν=Σρ=Σ<ιΛ>

V V V

где последняя сумма должен быть распространена по всем элементарным связанным зарядам, находящимся в объёме V. Следовательно, если рг d R

^{у 1 =} Έ

есть скорость ΐ-го заряда, то

jrf^PdF=fw^dF=^i_iV_i-fjdV

V V ^V V

[ср. ур-ие (9)], откуда следует, что J=~. Полное выражение для j_M0Jl. имеет вид яр

1 мол.=^{с rot 1} щ · (50а)

Т. о. среднее макросцопич. значение полной истинной плотности токов j_MUKp0 равно сумме средних значений плотности токов проводимости J„p. “ токов молекулярных

j микро —jnp. "Ь 1мол. — 1пр. "b с rot + ^. (51)

С помощью ф-л (46) и (49) легко уже найти искомые ур-ия макроскопич. поля. Действительно, усередняя ур-ия (I⁷)—(IV) поля макроскопического по физически бесконечно малому объёму, принимая во внимание, что среднее значение дЕ т производных ит. д. равно соответствую-

- щим производным от средних значений Е и //, и обозначая для краткости истинные микроскопии. значения величины звездочками (ρ“, j“, E“, Η*), а их средние микроскопии, значения чер-

сверху, получаем:
, 1 дН* rot Е*=—,	(Ia)
rot ff* - ± + i? 7*=+ ΓΟΙ /7 с dt "Г с J с dt ^
4πτ-, ,. Ьл дР + TJ„p.+ inrotI+TW,	(Па)
div E*=4πρ*=!±щсвбд — 4л div Ρ,	(Ша)
div Я*=0.	(IVa)

Таковы искомые макроскопич. уравнения поля. Обычно они записываются в несколько иных обозначениях. Среднее значение напряженности микроскопии, электрич. поля называется в макроскопич. теории просто напряженностью этого поля и обозначается просто через Е:

Ё=Е. (52)

Вектор

D=Е + ЬлР=Е + ^г±пР (52)

называется индукцией электрического поля (иногда также электрич. смещением). Среднее значение напряженности микроскопии, магнитного поля называется однако не напряженностью магнитного поля, как следовало бы ожидать, а его индукцией и обозначается буквой В:

Н*=В,

тогда как напряженностью магнитного поля в макроскопич. теории называется следующий вектор, обозначаемый буквой Н:

Н=Н* Ш=В-ЬЛ. (52")

Это нерациональное с современной точки зрения наименование магнитных величин взято из старых теорий магнетизма, основывавшихся на представлении о существовании особых магнитных зарядов. Наконец в макроскопической теории величины j_n и Q_ce6d. обозначаются просто через ρ и /.

В этих обозначениях ур-ия (1а)—(IVa) после некоторых простых преобразований приобретают вид:

^rot£=-Tsr; <^1б>

^rot"=4-f + T* (^ш>

divZ)=4?τρ; (Шб)

div В=0. (IV6)

Эта система ур-ий не будет однако полной, то есть не будет однозначно определять течение электромагнитных процессов по заданным начальным значениям характеризующих поле величин, если ее не дополнить нек-рыми ур-иями, устанавливающими дополнительные соотношения между этими величинами. Связь между j и Е устанавливается попрежнему ур-ием (Vэ.):

J=У (Е + Е_спюр.). (V6)

Далее из (50а) и (42). следует:

D=Е + 4πΡ=(1 + 4πα) Е (Vila)

или

D=εΕ, (VII б)

где коэфициент ε=1 + 4па носит название д и-электрической постоянной (диэлектрическая проницаемость среды) и наряду с γ характеризует собой электрические свойства данного вещества. Что же касается связи между Н и В, то в ферромагнитных телах (железо, «икель и тому подобное.) никакого однозначного соотношения между Н и В не имеется. Вообще электромагнитные явления в ферромагнитах по своей сложности выходят за пределы Максвелловой теории поля. В неферромагнитных телах намагничение пропорционально полю Н:

= Ш, (53)

причем в зависимости от знака коэф-та к, именуемого магнитной восприимчивостью, различаются тела парамагнитные (к>0) и диамагнитные (&<0). Из (53) и (52") следует:

В=Н + 4л=(1 + 4 л к)Н,

или

В=μΗ, (VIII)

причем коэф. μ=1 + 4лА: носит название магнитной проницаемости и характеризует собой магнитные свойства данного вещества. Ур-ия (16)—(V6) и (VII6) —(VIII6) представляют собой систему ур-ий макроскопич. поля в указанном выше смысле слова и носят название ур-ий Максвелла для весомых тел. Полагая в этих ур-иях ε=1 и μ=1, мы в качестве частного случая их вновь получаем наши исходные макроскопич. ур-ия поля.

Наиболее существенное значение имеют следующие отличия ур-ий Максвелла для весомых

(52")

тел от ур-ий микроскопических. Во-первых, из сравнения ур-ий (16) с (1а) и с (I) следует, что

⁽⁵⁴)

L S

то есть что эдс индукции в произвольном контуре L определяется не изменениями магнитного потока H_ndS, а изменениями потока магнитной индукции через этот контур. Этим именно обстоятельством обусловливается та роль, какую играет в электротехнике железо (сердечники трансформаторов, обмоток генераторов и моторов и т. д.), так как в ферромагнитных телах магнитная индукция В достигает, как известно, значительно 66лыпих значений, чем в неферромагнитных. Во-вторых, ур-ия достоянного электрич. поля в однородном диэлектрике (то есть при ε=Const) принимают вид [см. также (VI16)]:

rot Е=0 и div D=div εΕ=ε div E=4πρ, или

div E=—.

ε

Сравнивая эти ур-ия с ур-иями постоянного электрич. поля в вакууме [см. (1а) и (Ша)] rot Е=0, div Ε=4πρ, убеждаемся, что при наличии одних и тех же свободных зарядов ρ поле в однородном диэлектрике в ε раз слабее, чем в вакууме (это положение к неоднородному диэлектрику совсем не применимо). Этим объясняется например значение диэлектриков при конструкции конденсаторов: заполнение диэлектриков пространства между обкладками конденсатора уменьшает напряженность электрического поля, а стало быть и разность потенциалов между обкладками, и тем самым увеличивает емкость конденсатора и уменьшает опасность пробоя.

Для полного охвата макроскопич. электромагнитных явлений необходимо дополнить уравнения Максвелла выражениями, определяющими величину сил, испытываемых помещенными в поле телами. Сила, действующая на неподвижный заряд q, попрежнему определяется ф-лой (2)

F=qE.

Сила, действующая на элемент тока проводимости j dV или I dl, получается из ур-ия (14а) путем усреднения по физически бесконечно малому объёму. Приняв во внимание (52"), получаем вместо (11а)

F=+[dl,B}. (55)

Наконец путем рассмотрения электронной структуры диэлектриков можно показать, что электрич. поле стремится втянуть их в области максимальной напряженности поля вне всякой зависимости от направления поля. Этим например объясняется притяжение кусочков бумаги или бузиновых шариков заряженными телами. Аналогично этому парамагнетики втягиваются магнитным полем в области максимальной его напряженности, тогда как диамагнетики, наоборот, выталкиваются из этих областей. Ур-ия Максвелла являются основными ур-иями электротехники и в общем и целом вполне правильно описывают все основные макроскопич. электромагнитные явления. Однако можно указать целый ряд таких явлений, для объяснения которых Максвелло-вы ур-ия оказываются недостаточными (дисперсия света, магнитомеханич явления и т. д.).

Лит.: Эйхенвальд А., Электричество, 8 изд. М.—Л., 1933: Поль Р., Введение в современное уче ние об электричестве, пер. с нем., 3 изд., М.—Л., 1933; Тамм И., Основы теории электричества, т. 1, 2 изд., М.—Л., 1932; Abraham М., Becker R., Theorie d. Elektrizitat, Lpz.—В., 1925—30; Cohn E., Das elek-tromagnetische Feld, 2 Aufl., B., 1927; Frenkel J., Lehrbuch d. Elektrodynamik, В. 1—2, Berlin, 1926—28; Whittaker E., A History of the Theories of Aether a. Electricity, L., 1910. И. Тамм.