> Техника, страница 97 > Электрострикция

Электрострикция

Электрострикция, явление упругой деформации различных тел (в особенности диэлектриков) в результате воздействия на них пондер-моторных сил, вызванных окружающим электрич. полем. Как известно, на всякое тело, помещенное в электрич. поле, действуют силы электрич. происхождения, стремящиеся вызвать перемещения электрич. зарядов в теле. Однако тогда, когда такого рода перемещения невозможны (например в случае диэлектриков, помещенных в электрич. поле), эти электрич. силы действуют на само тело (то есть становятся пондермоторными). В результате внутри тела (например внутри диэлектрика) появляются натяжения и давления, вызванные как притяжением заряженных тел друг к другу, так и смещением электронов и ионов (под влиянием внешнего электрич. поля), что влечет за собой упругие деформации тел.

Впервые явления Э. констатировал Фонтана в 1831 г. Он заметил, что объём конденсатора в виде лейденской банки (и аналогичного рода приборов) увеличивается при электризации. Первое исследование явления Э. произвел в 1878 году Дутер, использовавший для этих целей прибор в виде особого рода лейденской банки (фигура 1). Прибор состоит из 2 сосудов: 1) внутреннего сосуда А с капиллярной трубкой Т и с электродом а и 2) внешнего сосуда В, также снабженного капилляром T и электродом b. Оба сосуда наполняются подкисленной водой, играющей роль обкладок конденсатора. При заряде такого конденсатора жидкость в капилляре Т опускается, в то время как в капилляре Т поднимается, что указывает на увеличение объёма конденсатора при заряде. В результате различных исследований такого рода и измерений было определено, что изменение объёма прямо пропорционально квадрату разности потенциалов и обратно пропопционально квадрату толщины стенок сосуда А. Все последовавшие затем многочисленные исследования и измерения величины Э. в статич. полях у изотропных тел (твердых,

Фигура 1.

г

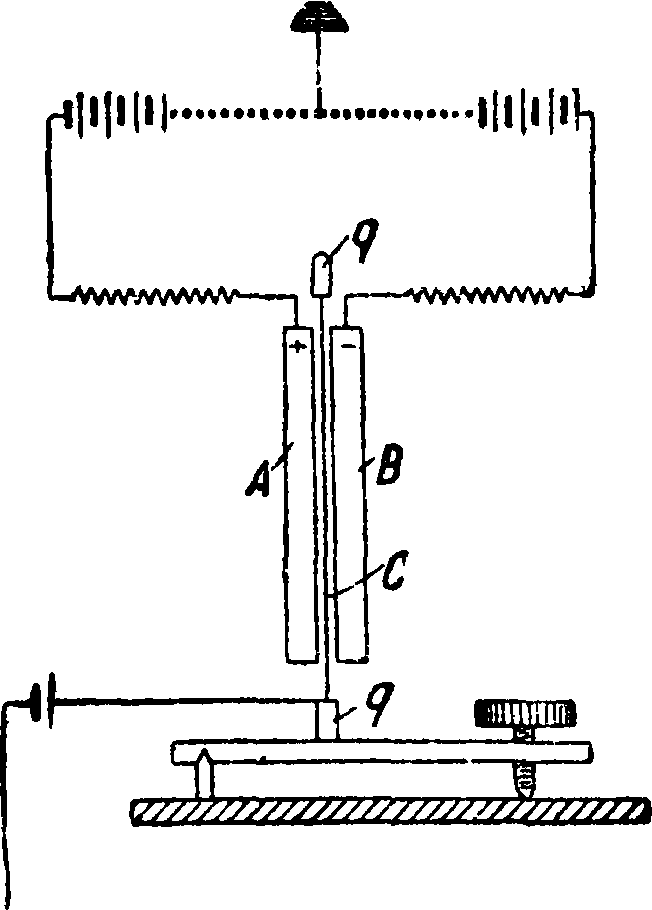
Фигура 9.

жидких и газообразных) показали, что для большинства тел величина деформации пропорциональна квадрату напряженности электрич. поля. Величина Э., вообще говоря, чрезвычайно мала, благодаря чему подробное исследование явления представляет значительные трудности. Относительно большой Э. обладают растворы, где замечается сжатие раствора вследствие производимого ионами электролитов притяжения соседних молекул. В газах изменение объёма Δν газового конденсатора при возникновении поля Е можно выразить ф-лой

Αν ^ V.. Е²,

8 тс др ¹

где V — потенциал конденсатора, р — давление промежуточного газа, е — диэлектрич. постоянная газа.

Особые качественные и количественные показатели обнаруживаются у кристаллов, обладающих пьезоэлектрическими свойствами (смотрите Пьезоэлектричество и Пьезокварц). Эти особенности состоят в том, что у пьезоэлектрич. кристаллов

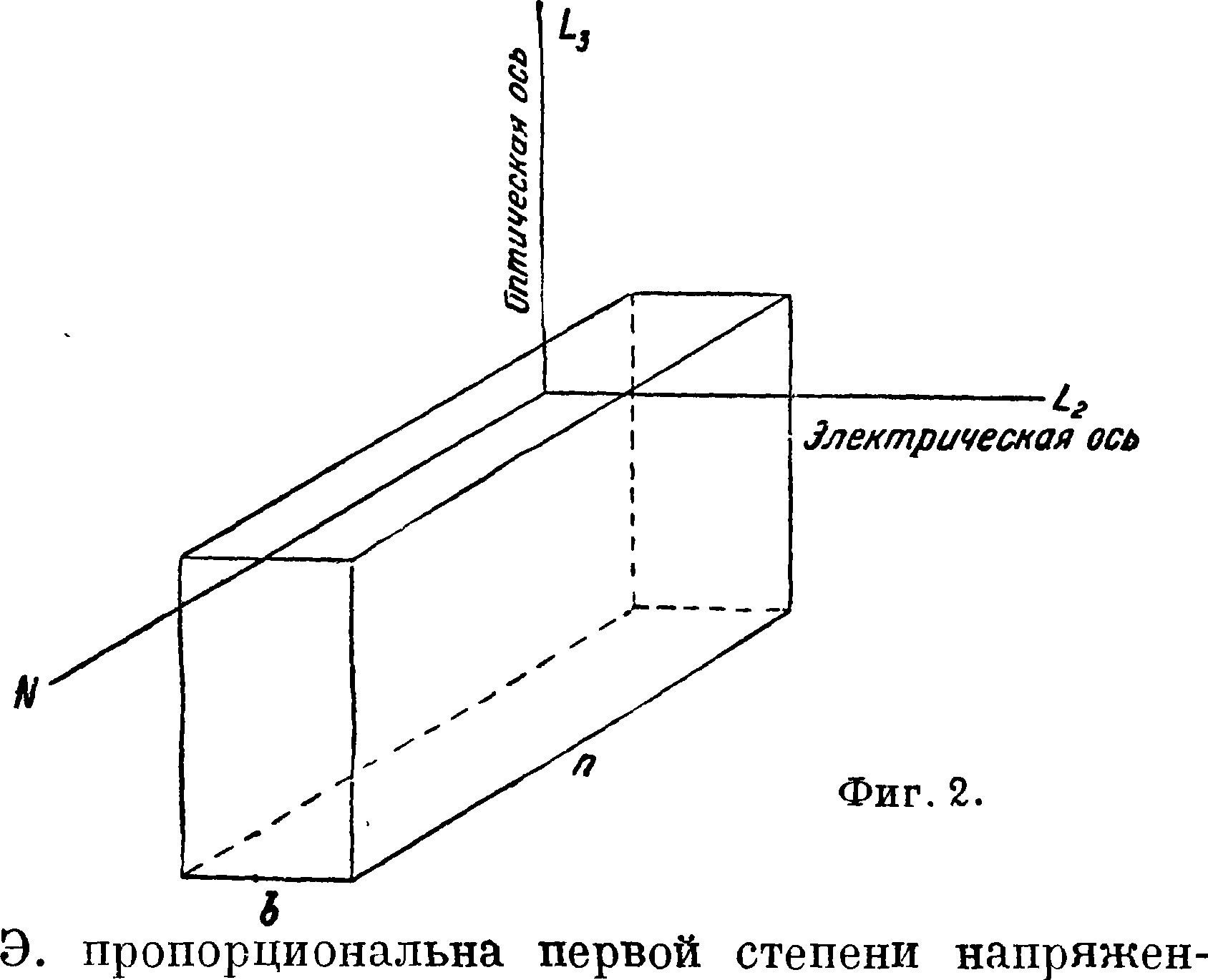
ности электрич. поля и что в различных направлениях величина Э. различна. Первая особенность, делающая у пьезокристаллич. тел эффект Э. значительно более заметным, создает условия для более широкого технического использования явления Э. этих тел. Вторая особенность дает базу для применения Э. в специальных целях. Так например, если сообщить двум противоположным граням пластинки (вырезанной в форме параллелепипеда согласно фигура 2 из пьезокварца), нормальным к электрич. оси, разность потенциалов V, то пластинка получит а) удлинение вдоль по оси электрической:

= KV

и Ь) укорочение вдоль по нормали Ν:

Δ^=-*·Τ · ^V

с) вдоль же по оптич. оси Δ^₃=0. Здесь К — пьезоэлектрич. постоянная кварца, b — размер параллелепипеда вдоль электрич. оси и п — то же вдоль оси Ν. При V ^ 6 000 V Δ/_х ^=1,2 · 10^_б сантиметров если же изготовить кварцевую пластинку так, чтобы п — 100 6, то

Δ/₃ ~ — 1,2 · 10~⁴ см.

Следовательно даже у пьезокристаллов, обладающих большим эффектом Э., изменения размеров при Э. оказываются столь малыми, что для их определения, и измерения являются йедостаточно точными даже оптич. методы. Здесь

ίΤ. Э. Доп. т. получили применение специальные приборы, разработанные Кюри, в частности так называемым пресс с пьезоэлектрич. манометром и прибор с увеличивающим рычагом и микроскопом. Если к рассмотренной выше пластинке пьезокварца, вырезанной в форме параллелепипеда, приложить переменное электрическое поле, то пластинка будет деформироваться одновременно с изменением этого поля, то есть начнет вибрировать. Амплитуду колебаний пластинки (параллелепипеда) можно значительно увеличить, если приложить переменное поле частоты, равной собственной частоте пластинки (смотрите Резонанс). Гл. обр. на последнем явлении и .основано большинство практич. применений Э. Согласно данным теории упругости ф-ла, связывающая размеры и свойства упругости стержня или пластинки, отвечающей укороченному стержню (если на концах пластинки находятся пучности акустич. волны, а узел лежит в середине стержня), имеет вид:

N=—λί ^Е—9-

21 V q ^,

где N — число продольных колебаний в ск., I — длина пластинки в направлении колебаний в см, Е — модуль упругости, g=981 см/ск и q — плотность вещества пластинки. (Та же формула действительна и для случая, когда у широких граней пластинки получаются узлы стоячей полуволны, а у середины ее толщины — пучность.) Таким обр. для вырезанной из кристалла пьезокварца пластинки толщиной I=1 сантиметров при q — 2,65 и Е_bг — 7 850 килограмм/мм² имеем: N —=269,531 колебаний в ск. Пластинка, имеющая форму параллелепипеда, как известно, обладает тремя собственными частотами и значительным количеством обертонов. Пластинки, имеющие круглую форму, также имеют три собственные частоты. Эмпирические ф-лы, определяющие собственные частоты пластинки, вырезанной перпендикулярно электрич. оси кристалла так, что оптич. ось кристалла является одним из диам. диска, имеют следующий вид:

iV_r =

2 870. _N _ 2 715

d ’ ^iV2 ~ D

И

дт _ 3 830

^iVs ΊΓ~ >

где Ν — частота в kHz, d— толщина диска в миллиметров и D — диаметр диска в миллиметров. Наконец следует иметь в виду, что кварцевые пластинки обладают еще рядом собственных частот, гораздо меньших, чем те, которые зависят от длины стоячих акустич. волн в них, обусловливаемых поперечными колебаниями пластинки, аналогичными колебаниям струны.

Эффект Э. в сочетании с пьезоэлектрич. эффектом встречается в пьезоэлектрических крист и находит применение в целом ряде областей современной техники. Из всех известных пьезоэлектрич. кристаллов особо широкое применение нашел кварц (Si0₂) и в меньшей мере турмалин и сегнетовая соль (NaK₄C₄H₄0₆ · 6Н₂0). Последнее обусловливается значительными пъезо-и электростриктивными эффектами, большой ме-ханич. прочностью, а также рядом других качеств (малый темп-рный коэф., наличие относительно богатых месторождений и тому подобное.), свойственных пьезокварцу. Большинство практич. применений эффекта Э. кварца связано с явлением увеличения Э. при резонансе в несколько тысяч раз по сравнению с Э., создаваемой статич. полем. Так например, на эффекте увеличения емкости пьезокварцевого конденсатора по мере приближения частоты внешнего поля к одной из частот пластинки кварца основаны различные ва-

39

рианты некоторых из современных типов чувствительных частотомеров (смотрите Частоты измерения). Современные эхо-лоты для определения морских глубин и нахождения различных тел, а также ультраакустическая подводная связь и ряд других приборов целиком основаны на мощном акустическом излучении со стороны кварца при резонансном эффекте Э. Так, в частности уже при напряжении на электродах кварцевой пластинки порядка 30—40 kV в воде создается звуковой луч, убивающий рыбу и вызывающий резкую боль в руке, поставленной в направлении луча. Современная техника ультразвуковых волн (смотрите Ультразвуковые колебания) и ее развитие в большой мере связаны с Э., в частности с явлением Э. кварца, дающего новое мощнде орудие для широких акустич. и ультраакустич. исследований. Сюда относятся также кварцевые телефоны, репродукторы, специальные осциллографы (с чувствительностью, дающей на шкале, стоящей на расстоянии 1 ж от зеркала, смещение в 1 сантиметров при напряжении в 2,5 V), специальные стабилизаторы частоты в радиотехнике (смотрите Стабилизация частоты), вольтметры высокого напряжения и тому подобное.

Лит.: Хвольсон О., Курс физики, т. 4, стр. 258, Берлин, 1923; Болдырев А., Кристаллография, 3 изд., Л., 1934; Sacerdote, «Journ. de Phys.», P., 1899, t. 8, p. 457; ibid., 1899, p. 200; «Phil. Mag.», 1901, v. 1, p. 357; Kemble, «Physical Review», 1916, γ. 7, p. 614. А. Вайнберг.