> Техника, страница 94 > Эллипс

Эллипс

Эллипс, замкнутая плоская кривая 2-го порядка, сумма расстояний от каждой точки которой до двух данных точек, называемых фокусами, есть величина постоянная, равная длине 2а большой оси Э. (смотрите Конические сечения).

Из определения следует, что например

NF+NF_±=2a₉ (1) причем NF и NF_Xназываются радиусами -векторами точки N (фигура

1). Если за оси координат примем оси Э., то получим каноническое ур-ие кривой:

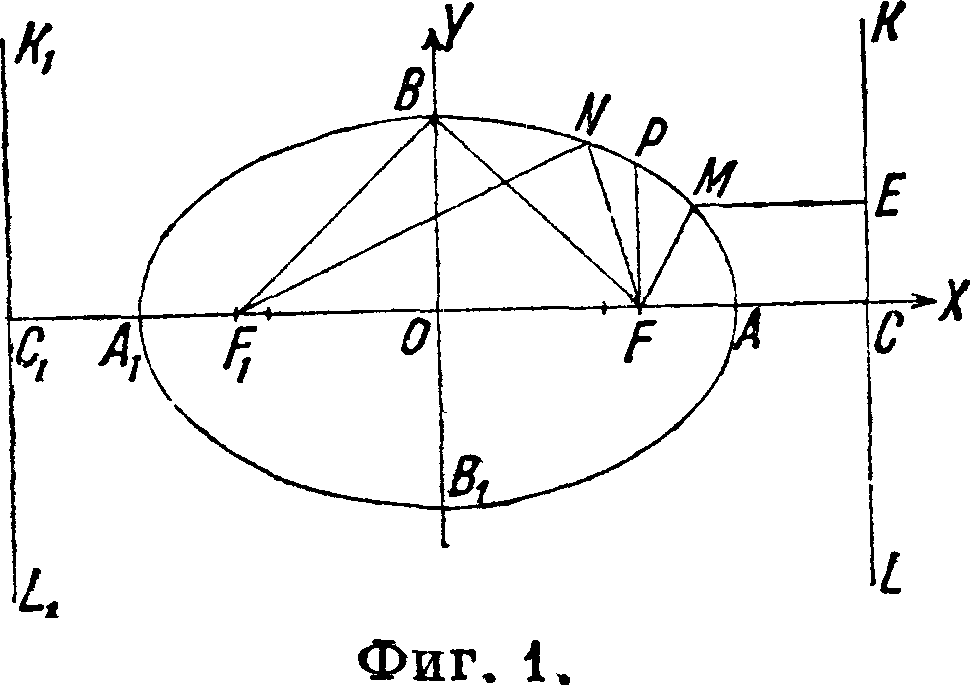
«2 2/2 _ 1 (22 "1" 52 В

где а (= О А=О А₁ — BF=BF _г) — большая полуось Э. и b(=ОВ=ОВ_Л)—малая полуось. Если междуфокусное расстояние FF₁=2ⁿ,

то называется эксцентриситетом

Э. Прямые KL и К_гЬ_г, ур-ия которых х= — и

a^{2 C}Q

х=— —, называются директрисами Э.,

причем отношение расстояний какой-либо точки Э. от фокуса и от соответствующей директрисы есть величина постоянная, равная ε, например

MF

МЁ

с а

= «(<!).

Радиус ы-в е к т о р ы любой точки (х, у) Э.:

г=а — ~х=^а —^£Х,

г_±=а А=а 4- еж.

Площадь Э.

Q=паЬ.

Полярное ур-ие Э. (фигура 2): 1) по отношению к центру О:

~ i - «² cosHp»

2) по отношению к фокусу F:

^ 1 + eCOS^’

где V—величина фокального параметра PF (фигура 1):

Р= ^-=α(1-ε²).

Параметрические уравнения х=a cos а у— b sin а (5)

выражают связь Э. с вписанным и описанным кругами (фигура 2). Сопряженные диа

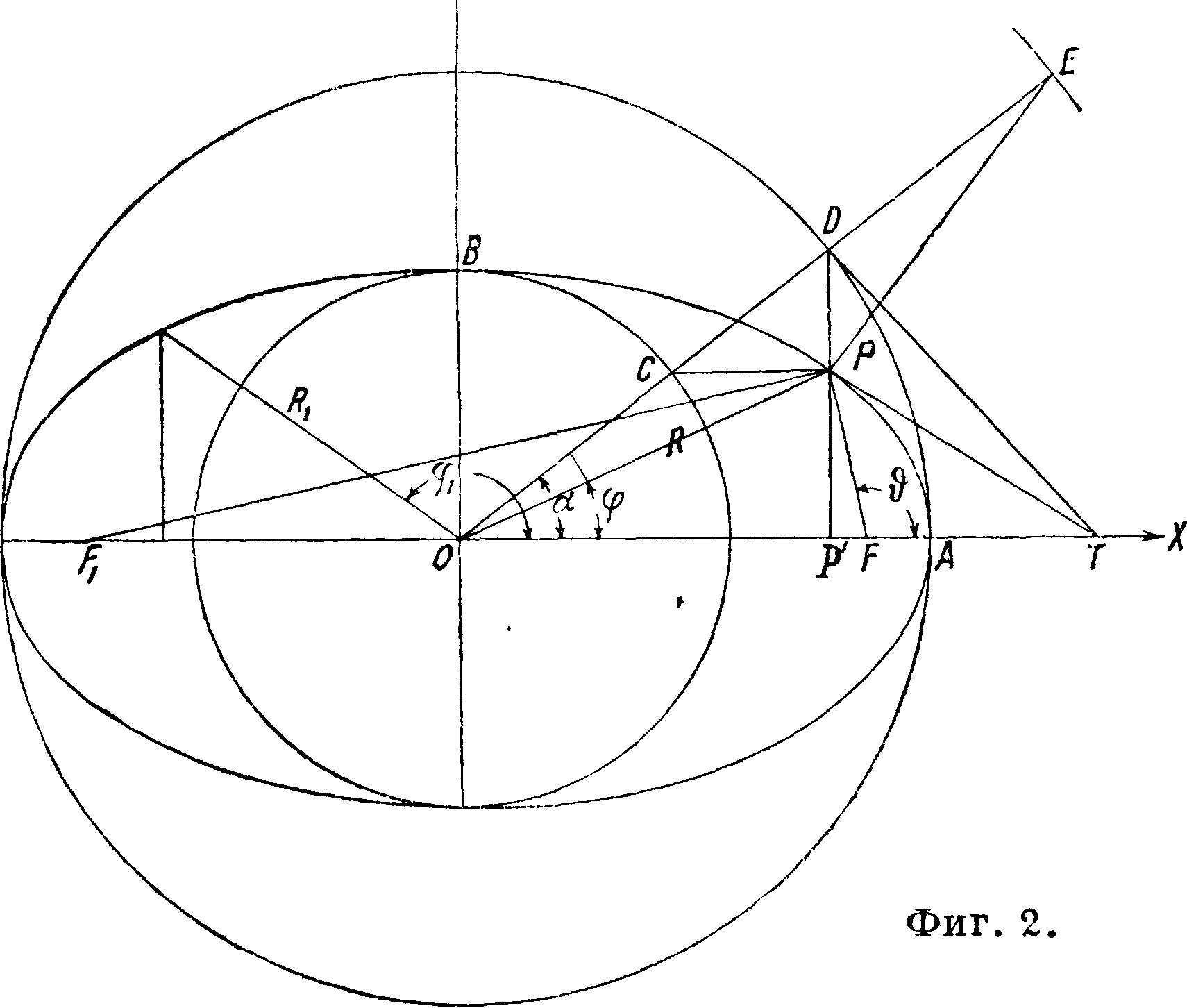
метры: один из них делит пополам хорды, параллельные другому; касательные в концах одного диаметра параллельны другому. Если Ψ и φ_Λ—углы обоих сопряженных диаметров с положительным направлением оси ж-ов, то

Ь²

Ч<Р · tg <Ρι=— -

У p-и е касательной в точке Р (х₀, у₀)

ХХр, УУр __ ч а² Ь²

Касательная РТ к эллипсу в точке касания Р делит пополам угол между радиусами-векторами той же точки. Касательные в концах хорды пересекаются в точке того диаметра, к-рый сопряжен с направлением хорды. Хорда есть поляра точки пересечения касательных; если х_г, у_г—координаты последней“, то ур-ие поляры выразится:

хх i, тi ₁а² "г _bг J"

Радиус кривизны: в вершине А

в Еершине В

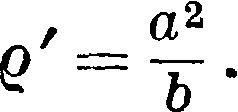
Построение 3. По полуосям а и b. а) Находят фокусы и наносят точки Э., пользуясь зависимостью (1). б) Соответственно соотношениям (5) из центра О описывают окружности радиусов Ь, а и Ь- -а и через точки С и 1>

(фигура 2) пересечения произвольного радиуса ОЕ остальными двумя окружностями проводят прямые, параллельные осям координат; точка пересечения Р этих прямых принадлежит Э.; нормаль его ЕР. в) Перемещают отрезок о.Ab так, что его концы скользят по осям координат; точка деления (на отрезки а и b) опишет Э. Построение касательной к Э. в данной точке, а) В точке Р Э. (фигура 2) делят пополам угол между радиусами-векторами этой точки,—биссектриса угла и является касательной к Э. б) Находят точку Т пересечения с осью абсцисс касательной к окружности в точке Р, соответствующей Р. Прямая РТ—искомая касательная. Нахождение центра, осей и фокусов вычерченного Э. Проводят 2 пары параллельных между собой хорд АА_1УΒΒ_Ί и СС₁₉ ВВ_Л (фигура 3). Прямые ΜΝ и KL_yпроведенные через средины каждой пары хорд“ являются диаметрами Э., их пересечение О

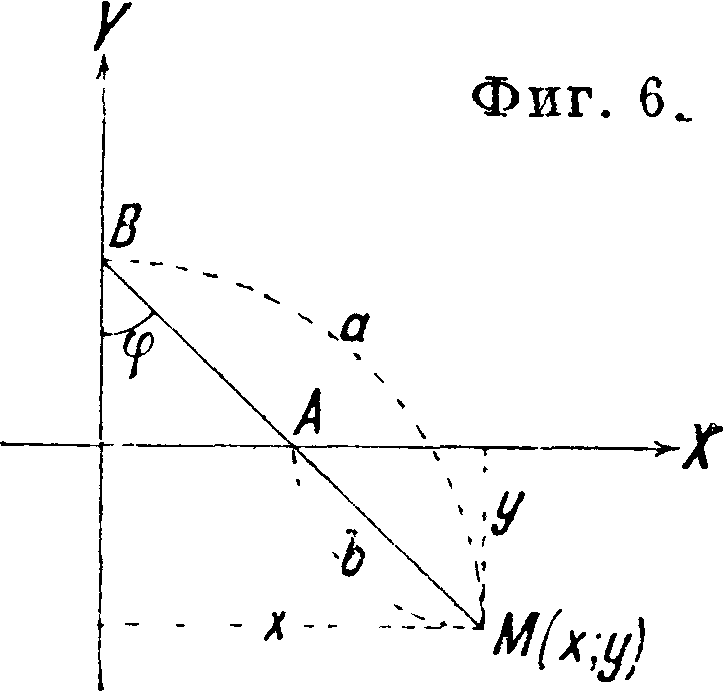
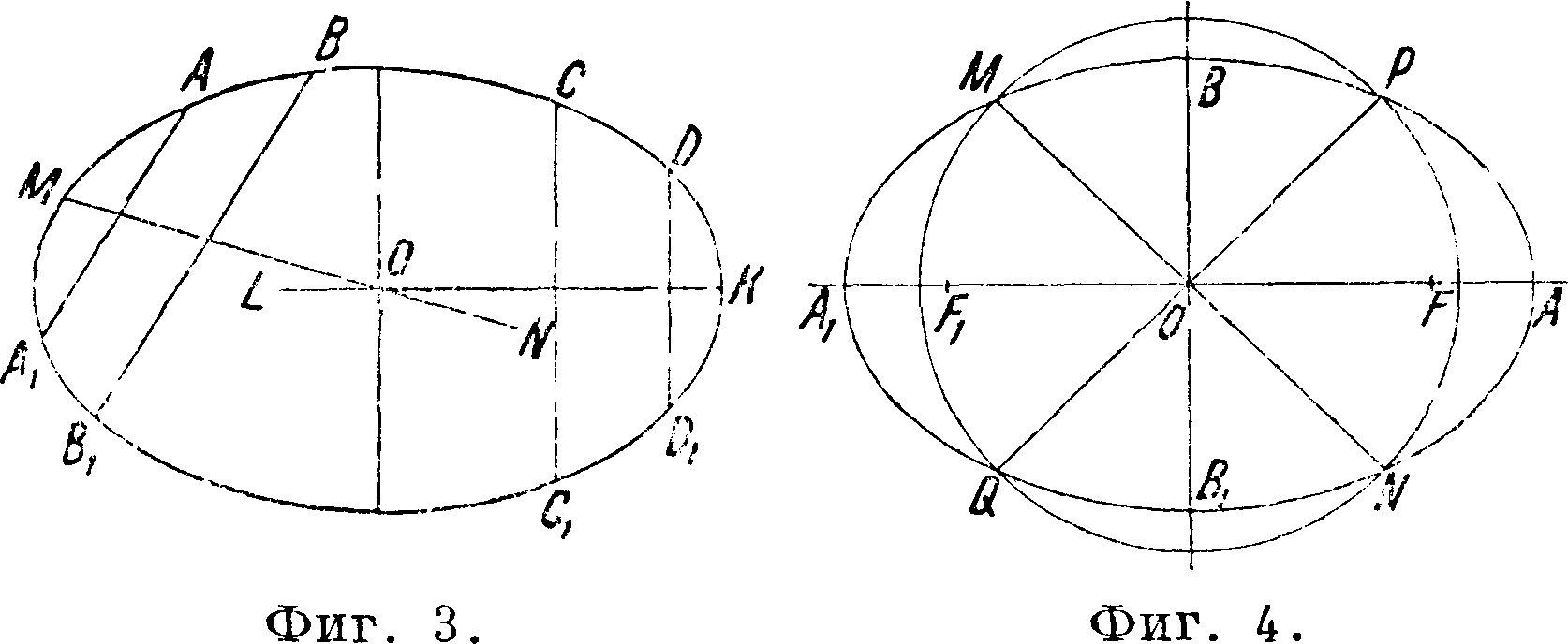
определяет положение центра Э. Из найденного центра описывают окружность радиусом, большим малой оси, но меньшим большой оси. Соединив полученные точки М, JV, Р, Q пересечения окружности с Э., как указано· (фигура 4), делят пополам образовавшиеся углы, биссектрисы их являются осями Э. Наконец окружность, описанная из В радиусом, равным О А, пересечет А А, в точках F и Е — фокусах Э.

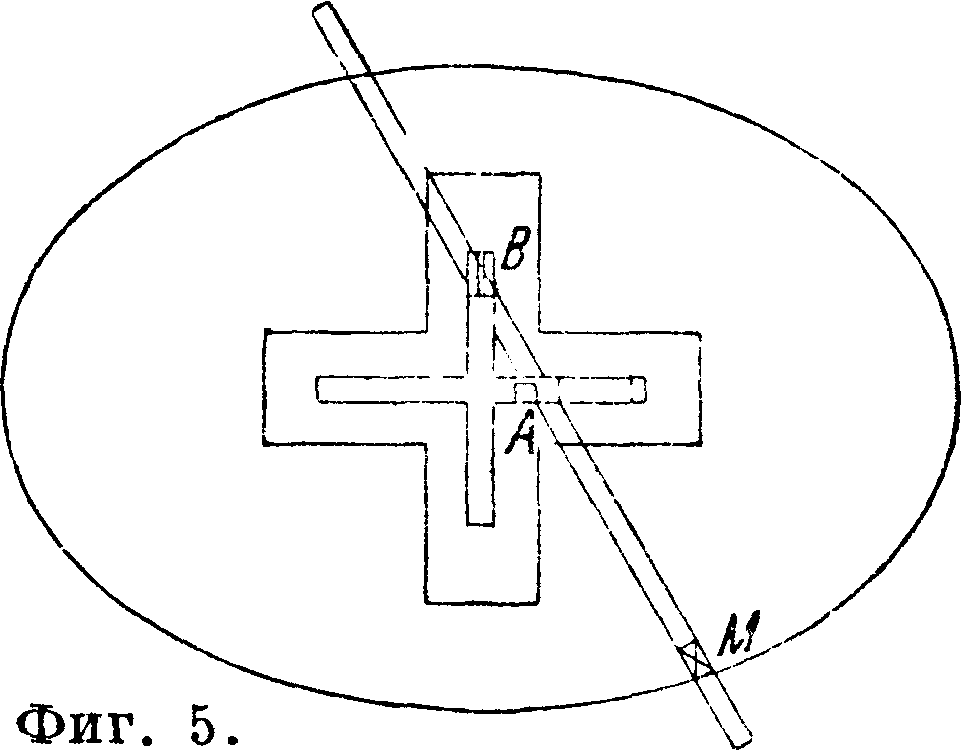
Эллиптический циркуль. В ме-таллич. доске (фигура 5) сделаны два прореза поя прямым углом; в них ходят ползуны, к которым прикреплена шарнирами А и В линейка АВ. Закрепленный при помощи муфты М в любом месте линейки карандаш будет вычерчивать Э. Действительно, если отрезки МА и МВ (фигура 6) обозначают соответственно а и b, то ж=а sin ψ

и у=b cos φ или ~=sin ψ и ~=cos ψ, откуда

+ |i=(sin² φ + cos² ψ)=1,

следовательно точка М (х, у) принадлежит Э. Если линейку закрепить неподвижно, а крестовине вместе с прикрепленным к ней ом, в к-рый вставлена обтачиваемая вещь, придать движение, то резец, помещенный в точке М, <5удет обтачивать по эллипсу. Такое устройство имеет столик () Леонардо да-Винчи для

•ВЫТачИВаНИЯ 3. В). Никаноров.