> Техника, страница 97 > Эллипсоид инерции

Эллипсоид инерции

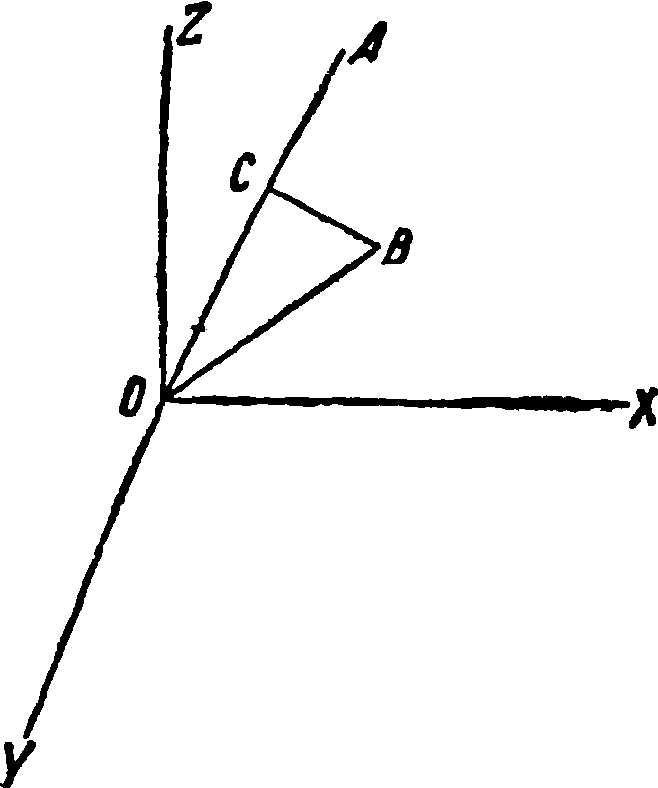
Эллипсоид инерции, поверхность, которая дает картину изменения величины момента инерции тела в зависимости от изменения направления оси, проходящей через начало координат. Взяв на расстоянии г от начала координат произвольную переменную точку В тела, имеющую массу dm, выразим момент инерции тела, относительно оси О А (смотрите фигуру):

Ia=JV dm,

где ρ — расстояние ВС точки В от оси АО. Если α, /?, у — углы, образуемые осью О А с осями координат, и х, y_t ζ — координаты точки В, то, как известно,

ОС — #cosa + ycosβ + zcos у и

Г²=X² -f у² -f- ζ².

Определяя ρ из тр-ка ОВС

ρ²=г² - СО²,

получаем для момента инерции выражение

1α= J[(я² + У² + ζ²) — (х cos а + у cos β +

+ 2cos у)²] dm.

После очевидных преобразований подинтегральная ф-ия примет вид:

(1 — cos²a) х² -f- (1— cos² β) у² + (1 — cos² у) ζ² — — 2yz cos/? cos у — 2xz cos a cos у — 2xy cos a cos β.

На основании известного соотношения cos²a + cos²/? + cos² у=1

заменяем коэф-ты при х², у², ζ² соответственно через

cos²/? + cos²y, cos²a -f- cos²y, cos²a -f- cos²/?

и группируем, вынося за скобки cos²a, cos²/?, cos²y:

(у² -f- z²) cos² a + (x² -f- z²) cos² β -f-+ (x² - ry ²) C.OS² у — 2yz cos β cos у —

— 2xz cos a cos у — 2xy cos a cos β.

A T. к.

(y² -f- z²) cos² a dm=cos² a J y²dm -f-+ cos² a Jz²dm — cos² a (I_y + I_z)=I_x cos ²a,

J (x² + z²) cos² β dm=I_y cos² β,

x² + у²) cos² у dm — I_z cos² y,

TO

IA — Ιχ ^{Cos2 aJ}rIy ^COs2 β + Iz ^cos2 У ~~

— 2I_yz cos β cos у - 2I_xz cos a cos у —

— 2I_xy cos a cos β, (A)

где I_xy=/xydm ит. д. Итак, первые 3 коэф-та— моменты инерции относительно координатных осей, последние же 3 коэф-та — центробежные моменты инерции; они не зависят от направления- оси О А. Т. о., зная I_x, I_y, I_z, I_yz, I_xz, Ixy,·можно определить момент “Инерции отно~ сительно любой оси, проходящей через начала координат.

Правая часть выражения (А) напоминает поверхность 2-го порядка, притом не имеющую бесконечно удаленных точек, так как 1_А вообще-не может обращаться в нуль (за исключением случая, когда тело имеет форму бесконечно тонг кого стержня и 1_А берется относительно направления этого стержня). Такой поверхностью м. б. только поверхность эллипсоида (в частном случае сферич. поверхность), поэтому преобразуем выражение (А), умножив обе части его на произвольный множитель к², на который наложим требование 1_А * к²=1, откуда

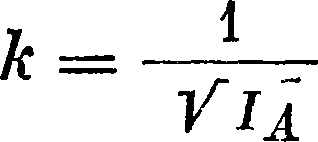
Выражение (А) примет вид:

I_xk² cos² a + Iyk² cos² β + I_zk² cos² у —

— 2I_yzk cos β · A cos у — 21 _xz к cos a · к cos у —

— 2I_xyk cos a · к cos β=1. (A)

Далее, если на оси ОА отложить от начала координат отрезок длиной к, то к cos a=х, к cos β — у, к cos у=ζ,

где х, у, я—координаты конца, отрезка, и (А) преобразуем в

1_хх^г + 1уУ² + М² — 2 I_yzyz — ΪΙ_Χ2χζ —

-Ч1_хуху =. (А")

Полученное ур-ие определяет поверхность, носящую название Э. и. Эту поверхность опишет конец отрезка к при изменении направления оси О А.

Если координатными осями будут служить три взаимно перпендикулярных направления

или главных диаметров поверхности, то, как известно, уравнение эллипсоида принимает более простой вид:

Ах² + By² + С z²=1. (Б)

Если ур-ие Э. и. приведено к виду (Б), то координатные оси называют главными осями инерции для данного начала координат, а соответствующие им моменты инерции — главными моментами инерции, следовательно в ур-ии (Б) А, В и С — главные моменты инерции. По отношению к главным осям центробежные моменты инерции равны нулю. Главные оси инерции, проходящие через центр инерции тела, называют главными центральными осями инерции, а моменты инерции относительно их — главными центральными моментами инерции. Обыкновенно в случае трехосного Э. и. координатные оси располагают так, чтобы А > В > С, то есть чтобы большая ось шла по OZ, средняя по 07 и наименьшая по ОХ; действительно, если уравнение Э. и. написать в виде

X², У², & _{= 1}

(ПУ (ПГ (VI) ~

то полуосями Э. и. будут являться 1 1 1 Va ’ Vb ’ Vc ’

Если А=В, то Э. и. будет эллипсоид вращения; при А — В — С он превращается в шар, то есть три главных момента инерции в любой точке тела одинаковы: 1_г — /_а=/₃=I. Так, для однородного круглого цилиндра (смотрите Момент, табл. 2) главные центральные моменты инерции таковы:

h=h=Т ^Мг* +12^тг’ ь=4 ^Μμ·

Условием равенства моментов является равенство_чMr* + ь Ml*=4- Mr“,

откуда г __ 1

I V3-

>

1

V2 ’

Отсюда величина сжатия выразится соотношением а —с V 2-1

с ^< У2

ИЛИ

а —с ^ 2-VT с ^< 2

которое показывает, чТо эллипсоид вращения не м. б. очень сплюснутым, растянутым же м. б.’ беспредельно (в случае бесконечно тонкого стержня Э. и. превращается в бесконечный круговой цилиндр). Т. к. радиус-вектор точек поверхно-стй эллипсоида (следовательно и соответствующий момент инерции) имеет экстремальные значения в направлении главных осей, то, если Э. и. дан ур-ием (А"), нахождение главных осей инерции сводится к нахождению экстремальных значений ф-ии (А), для чего можно приравнять нулю полный диференциал ее:

Лит.: см. Момент. В. Никаноров.