Ядро сечения

Ядро сечения, контур внутри площади поперечного сечения бруса, из пределов которого не должна выходить точка приложения сжимающей силы для того, чтобы в сечении не появилось растягивающих напряжений. Для сооружений, сложенных из камня или кирпича, например мостовые устои, фабричные трубы,

подпорные стенки (смотрите), ставится иногда обязательное условие, чтобы в сечении не возникали растягивающие напряжения. Это объясняется неодинаковым сопротивлением каменной кладки сжатью и растяжению. Выдерживая сжимающие напряжения, раствор, на котором сложена кладка, разрушается при небольших растягивающих напряжениях, и в швах кладки образуются трещины (так называемое «раскрытие шва»). Не будучи сами по себе опасны, при условии обеспечения устойчивости сооружения, эти трещины все же нежелательны, особенно в тех случаях, когда в швы кладки может проникать вода и, периодически замерзая i

и оттаивая, разрушать кладку. Из определения Я. с. следует, что если точка приложения сжимающей силы находится внутри него, то нейтральная линия проходит вне сечения бруса. Предельным случаем существования в сечении только сжимающих напряжений будет, когда нейтральная линия касается контура сечения; в этом случае точка приложения силы должна лежать на кон-туре, ограничивающем Я. с. Отсюда можно заключить, что контур Я. с. является геометрия. местом точек приложения сжимающей силы при касании нейтральной линии к контуру сечения бруса.

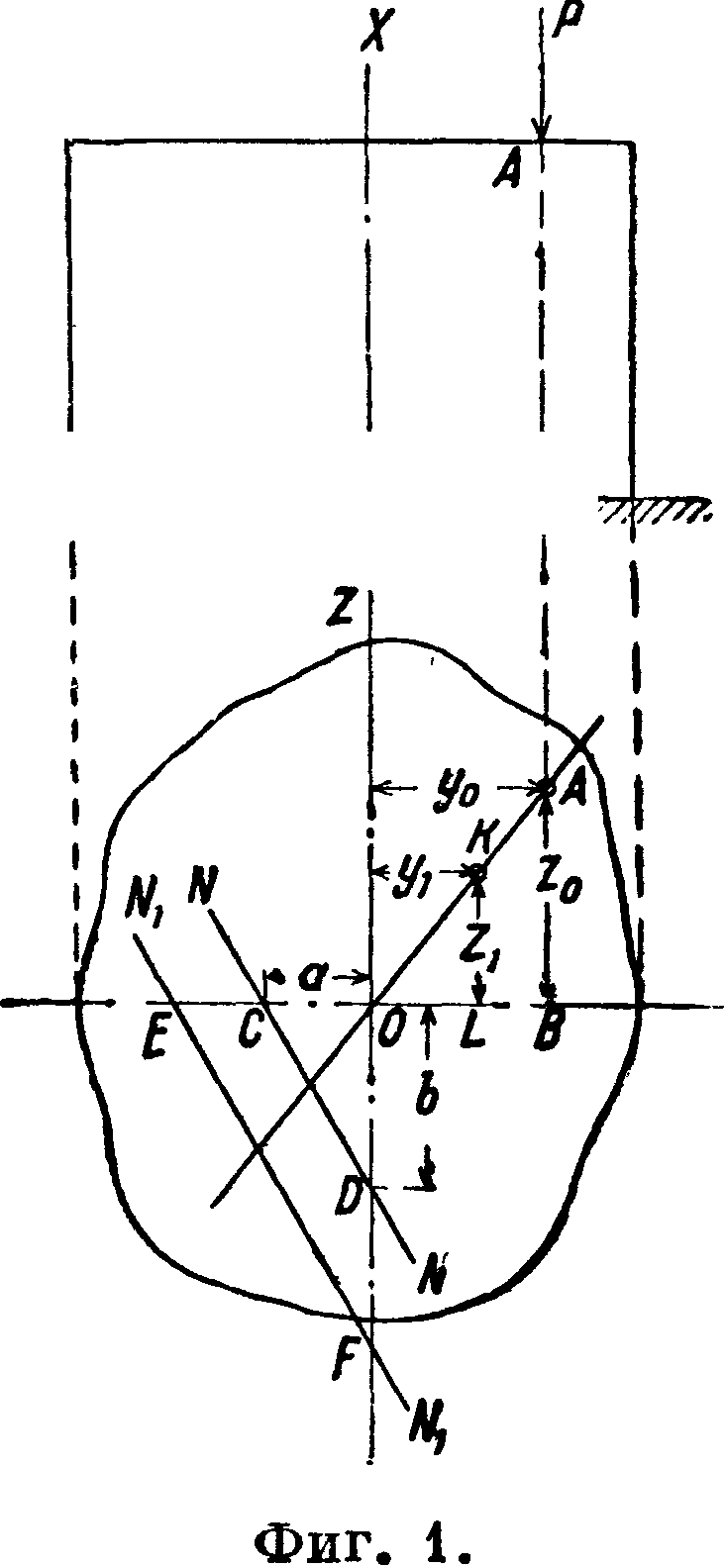
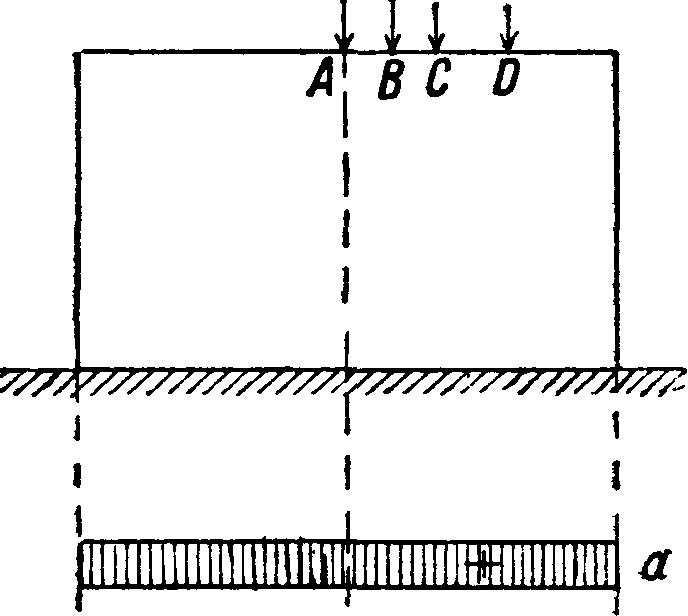
Пусть на брус (фигура 1) действует сжимающая сила Р, приложенная .в точке Я, не лежащей ни на одной из главных осей инерции.

Имея главные оси инерции OY и OZ, обозначим через y_Q и я₀ координаты точки А. Действие данной силы м. б. заменено эквивалентной ей системой из силы Р, приложенной в центре тяжести О сечения, и двух пар Py_Q и Pz_Q, действующих в главных плоскостях бруса YOX и ZOX (случай совместного действия изгиба и сжатия или т, н. внецентренное сжатие). В любой точке сечения с координатами у и z напряжение будет равно

Pvо.

(1)

Здесь F—площадь поперечного сечения, а 1_уи Ι_ζ—моменты инерции. Выражение (1) может давать положительные значения для напряжений (сжатие) или отрицательные (растяжение) в зависимости от знаков при у и z. Если воспользоваться зависимостями Ig-Fr^ и l_z=Fr, где Ту и г_ъ—радиусы инерции, то выражение

(1) можно преобразовать:

^{Г 4} 3 у

Приравняв напряжение нулю, нейтральной линии:

• ή (2)

получим ур-ие

1 +

V о

» + з-*=⁰·

Это—ур-ие прямой, отсекающей на осях Ζ отрезки:

ос=α= - ^ и OD=Ь=-

У о ^ζο

(3) Υ и

(4)

Т. о. каждой точке приложения силы (условно называемой «полюсом») соответствует вполне определенное положение нейтральной линии (на фигура 1—линия NN).

Следует отметить взаимность, существующую между координатами полюса у₀ и я₀ и отрезками а и b: если координатами полюса будут а и Ь, то нейтральная линия будет отсекать от осей отрезки:

^Г1 ^гу

“7 ⁼ УоИ -т⁼*о.

Если полюс будет перемещаться по линии О А, то нейтральная линия также будет перемещаться. Из равенства (4) легко усмотреть, что по мере приближения полюса к центру тяжести О, то есть при уменьшении величины у₀ и 2₀, отрезки а и Ь будут возрастать, и нейтральная линия будет удаляться. Когда полюс совпадет с ц. т. сечения, нейтральная линия удалится в бесконечность, и все сечение будет равномерно сжато (случац нейтрального сжатия). При удалении полюса от ц. т. нейтральная линия будет приближаться к нему, и в предельном случае, когда полюс будет в бесконечности, нейтральная линия пройдет через ц. т. сечения (случай простого изгиба).

Все нейтральные линии, соответствующие различным положениям полюса на линии ОА, будут между собой параллельны, в чем легко убедиться путем следующего рассуждения. Пусть полюс находится в точке К с координатами у_х и Тогда отрезки, отсекаемые нейтральной линией N₁N_1> будут равны:

ОЕ=а₁=~ — и 0F=— ^~· (5)

. У i Ч

Из подобия треугольников ОАВ и OKL следует: Уо ₌у±_я

2₀ Z i

Равенства (4) и (5) дают | ~ и ~=~. Сле довательно=~ и параллельность линий NN и N₁N₁ доказана.

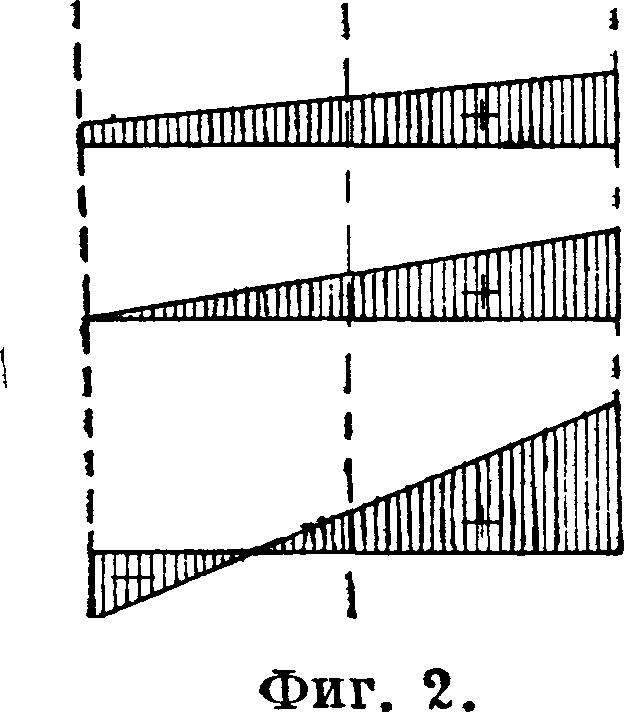
Разным положениям полюса соответствует распределения напряжений в поперечном сечении. Если сила приложена в ц. т. сечения—в точке А (фигура 2), то напряжение по всему сечению одинаково— а; если сила приложена где-нибудь внутри Я. с.— в *очке В,—то в сечении действуют сжимающие напряжения переменной величины Ь; при пдложении силы на контуре Я. с.— в точке С—распределение напряжений происходит по с и напряжения у одного края сечения равны нулю; при положении силы вне Я. с.—в точке D—в сечении действуют напряжения разных знаков d.

Для выяснения способа построения контура Я. с. следует рассмотреть зависимость между положением нейтральной линии и полюса при перемещении полюса по какой-нибудь прямой, не проходящей через ц. т. сечения. Пусть полюс перемещается по линии А_гА₂ (фигура 3), пересекающей главные оси OY и OZ в точках А_г и А_г. При положении полюса в А₁ (координа ты ОА_г, 0) нейтральная линия NN-l будет параллельна оси Z и отсечет на оси У отрезок

. При положении полюса в А₂ (координаты

0, ОА₂) нейтральная линия NN₂ будет парал-

г²

лельна оси У и отсечет на оси Z отрезок --·

^г ОА_%

Для всякого положения полюса А между точками Α_λ и А₂ можно Ζ заменить сжимающую

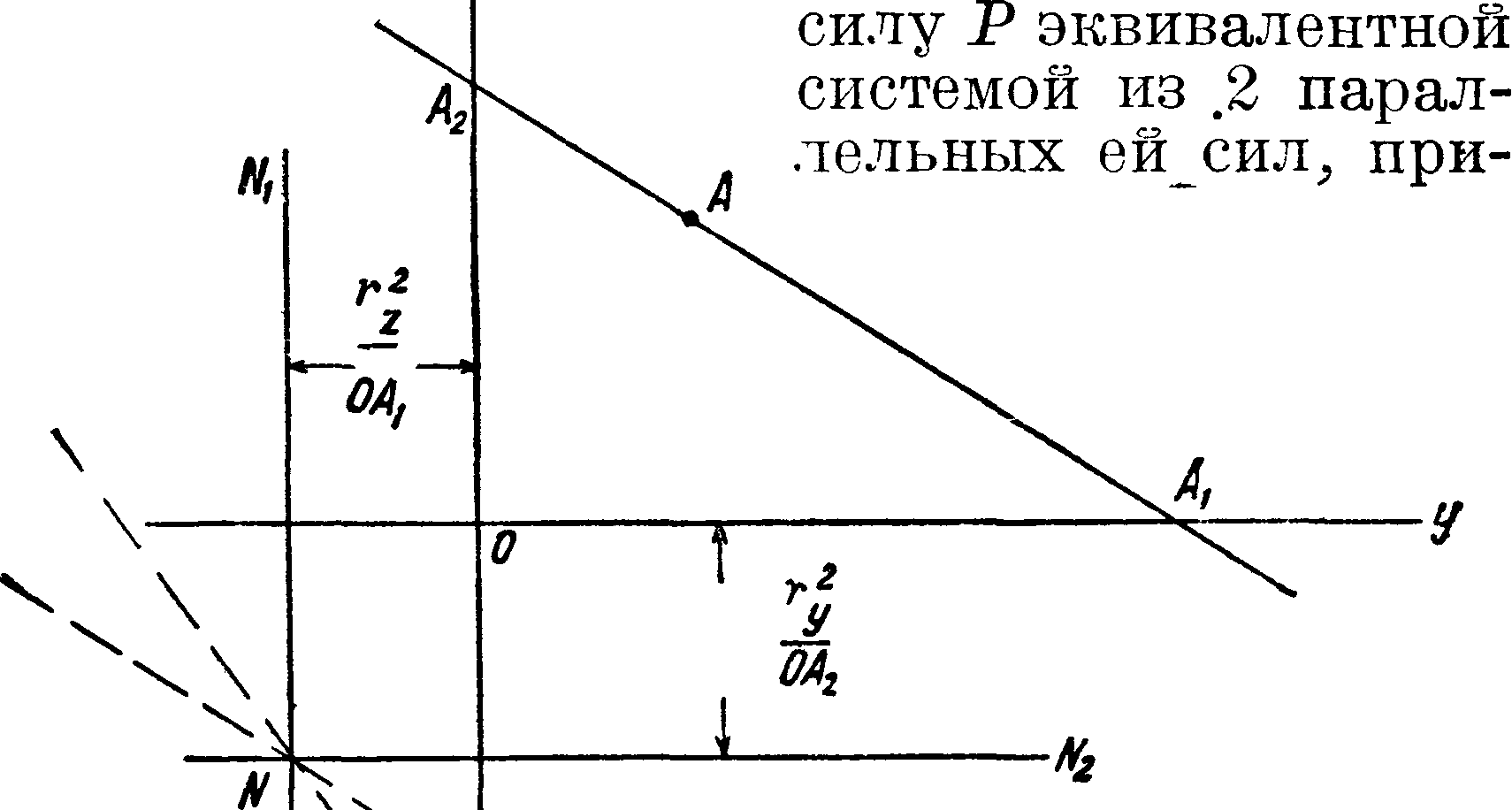
ложенных в А_х и А₂. Каждой из этих сил в отдельности соответствует своя нейтральная линия NNi или NN₂. -Очевидно, что через общую обеим линиям точку пересечения N будут проходить все нейтральные линии, соответствующие любому положению полюса А на линии

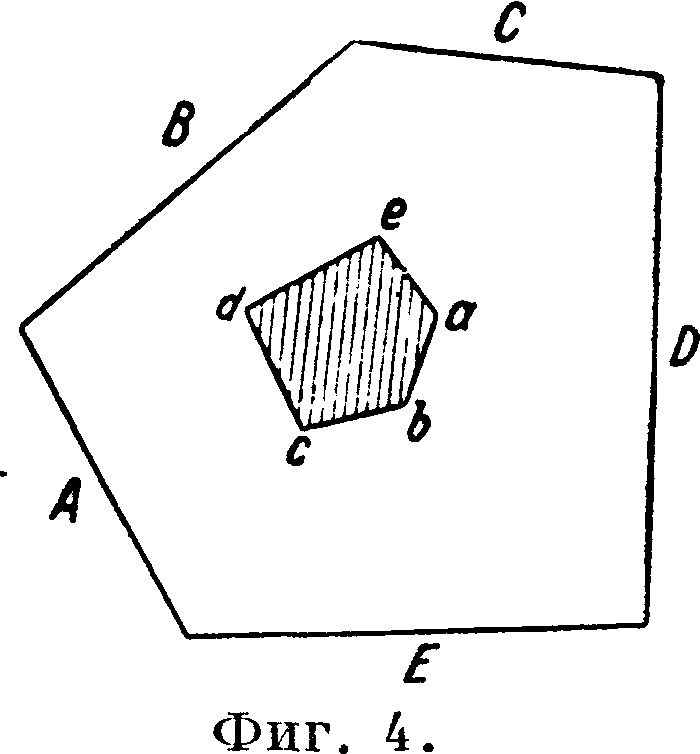
А_хА₂. Из указанного ранее свойства взаимности между координатами полюсами отрезками, отсекаемыми нейтральной линией, легко вывести, что для полюса в точке N нейтральная линия будет совпадать с линией А_гА₂. Следовательно, если полюс перемещается по Црямой линии, то соответствующая нейтральная линия вращается около некоторой неподвижной точки; и обратно, если нейтральная линия вращается около неподвижной точки, то соответствующий ей полюс движется по прямой, являющейся нейтральной линией для точки вращения, принятой за полюс. Т. о. для построения контура Я. с. надо провести к контуру поперечного сечения ряд касательных нейтральных линий и определить соответствующие им полюсы. Прямой линии контура сечения будет соответствовать вершина контура Я. с., а вершине контура сечения -будет соответствовать прямая контура Я. с. Для выпуклого многоугольного сечения Я. с. будет многоугольником того же порядка. Напр. для мн-ка ABCDE (фигура 4) каждой стороне А, В, С и т. д. соответствует точка Я. с. разный характер

Фигура 3.

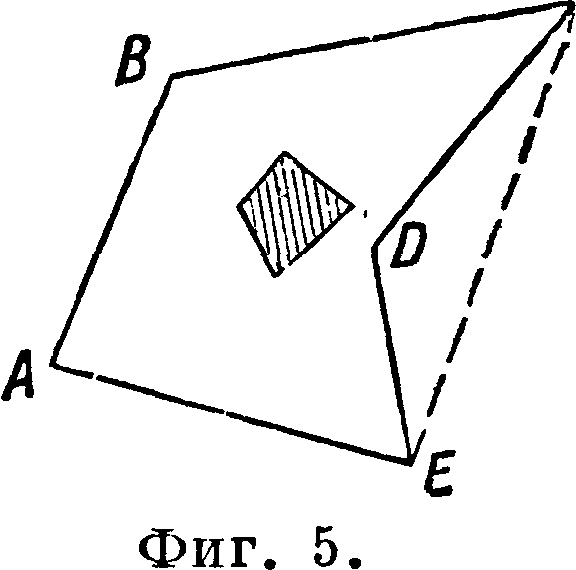
а, б, с и T. д. При переходе нейтральной линии из положения А в положение В полюс будет перемещаться по прямой аЬ, и таким образом, сколько сторон у поперечного сечения, столько же углов, а следовательно и сторон будет у контура ядра сечения. Для мн-ка с входящими углами, например ABCDE (фигура 5), надо строить ядро сечения для мн-ка АВСЕ, так как нейтральная линия не может занять положение CD или DE, то есть не может пересекать сечения.

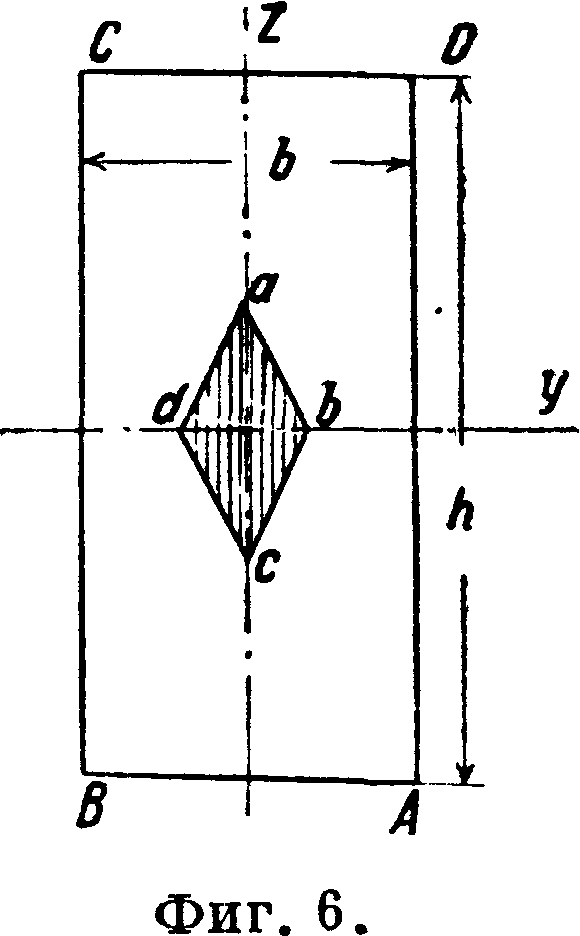
Для прямоугольника (фигура 6) вследствие симметрии сечения вершины Я. с. лежат на главных осях. Вследствие параллельности сторон прямоугольника главным осям для стороны АВ как нейтральной линии,

для которой £=— и точки а ядра сечения ур-ие (3) примет вид:

	1-^г?И=⁰’
откуда	1-^г?И=⁰’
	2г\| 2 F-rg 27 у 2 ^g° h Fh Fh	Wy_m⁼ F *	(6)
Момент	сопротивления относительно		оси У

^ПУ ~ h 2

_ ^ЬЛ² ·

-J 6 >

следовательно для точки а Я. с. ордината

Ь№ h π h

оън~ъ^я Для ^{точки с} аналогично #₀=— у Для точек b и (I у₀== ±^Ь~= ±. Дли ны диагоналей ac=~h и bЛ=%Ь. Следова-

О о тельно для того, чтобы в каменной кладке не возникали растягивающие напряжения,необходимо, чтобы равнодействующая нагрузок не выходила из средней трети сечения.

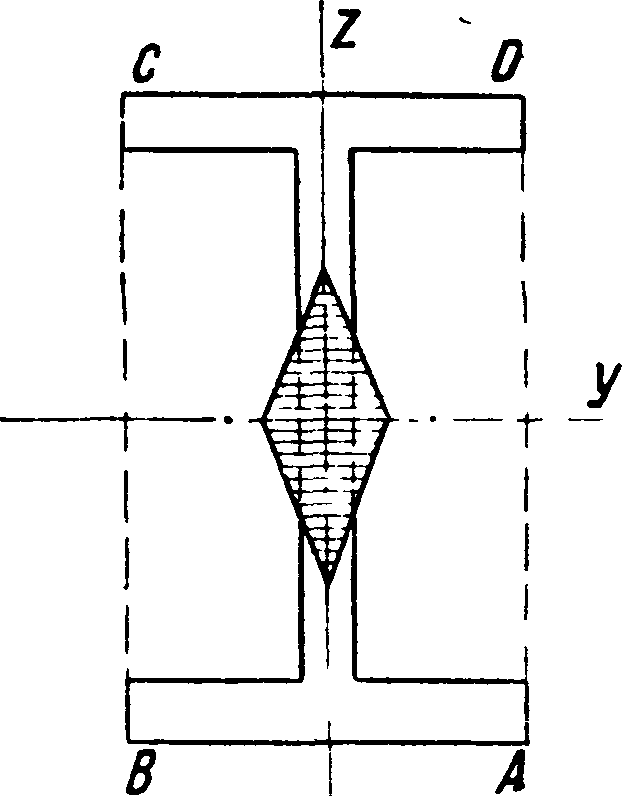
Для двутаврового сечения (фигура 7) нейтральная линия располагается по сторонам прямо-

Фигура 7.

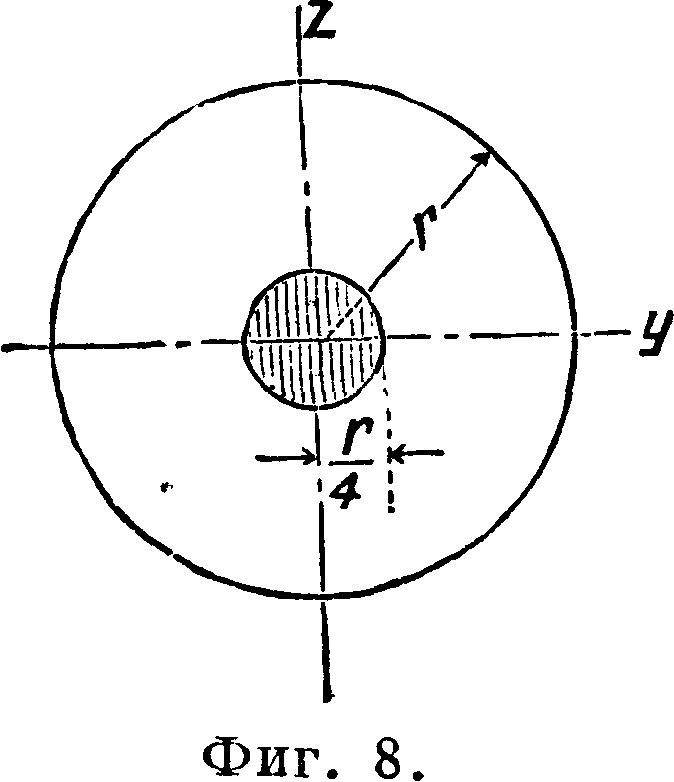
угольника ABCD и ядро сечения находится по той же формуле (6):

, w, w_z

го=± ; у о=± у >

где конечно W_y и W_s берутся,как для двутавра, а не как для прямоугольника.

Я. с. для круга (фигура 8) очевидно также •будет кругом, радиус которого z₀ определится аналогично предыдущему:

	_z - JL, So- _z’
где z=r, а	9 1 nri ₉ Г² ^r*=F ⁼ lT^:jir=T
откуда	Г² г
	*0=4? =Т

Лит.: Бобарыков И., Сопротивление материалов, ч. 1, М.—Л., 1930; Дружинин С., Сопротивление материалов, Л., 1930; Иванов Н., Сопротивление материалов, М— Л., 1931; Подольский И., Строительная механика, ч. 1, Сопротивление материалов, М., 1930; Проскуряков Л., Строительная механика, ч. 1, Сопротивление материалов, изд. 7, 1928; Р и в о ш О., Сопротивление материалов, ч. 2, изд. 2, МЛ., 1932; Тимошенко С., Сопротивление материалов, М.—Л., 1932; Худяков П., Сопротивление материалов, изд. 3, М., 1909. А. Лурье.